Complete Solutions to Example of chapter ATOMS, NUCLEI AND MOLECULES of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ATOMS, NUCLEI AND MOLECULES |
| SL ARORA | Example |
| Number Of Questions | 82 |
| Academic Year | 2023-24 |
In a head on collision between an alpha particle and gold nucleus, the minimum distance of approach is `4xx10^(-14)m`. Calculate the energy of of `alpha`-particle. Take Z=79 for gold.
View SolutionAn alpha particle with kinetic energy `10 Me V` is heading toward a stationary tin nuclcus of atomic number 50. Calculate the distance of closest approach (Fig . 3.23).
 .
.
View SolutionA beam of `alpha`-particle of velocity `2.1xx10^(7)m//s` is scattered by a gold foil (Z=79). Find the distance of closest approach of `alpha`- particle to the gold nucleus. for `alpha`-particle, `2e//m=4.8xx10^(7)kg^(-1)`.
View SolutionAn `alpha`-particle after passing through a potential difference of `2 xx 10^(6) V` falls on a silver foil. The atomic number of silver is 47. Calculaye (i) the kinetic energy of the `alpha`-particle at the time of falling on the foil (ii) the kinetic energy of the `alpha`-particle at a distance of `5 xx 10^(-14)` m from the nucleus and (iii) the shortest distance from the nucleus of silver to which the `alpha`-particle reaches.
View SolutionThe number of alpha particles scattered at `60^(@)` is 100 per minute in an alpha particle scattering experiment. Calculate the number of alpha particles scattered per minute at `90^(@)`.
View SolutionCalculate the impact parameter of a 5 MeV particle scattered by `90^(@)`, when it approach a gold nucleus (Z=79).
View SolutionA projectile of mass m, charge Z', initial speed v and impact parameter b is scattered by a heavy nucleus of charge Z. Use angular momentum and energy conservation to obtain a formula connecting the minimum distance (s) of the projectile form the nucleus to these parameters .show that for b=0, s reduces to the closest distance of approach `r_0`.
View Solutionfor scattering by an inverse square law field (such as that produced by a charged nucleus in Rutherford's model), the relation between impact parameter b and the scattering angle `theta` is given by
`b=(Ze^2 cot theta//2)/(4pi in_0(1/2mv^2))`
(a) What is the scattering angle for b=0?
(b) for given impact parameter, b, does the angle of deflection increase or decrease with increase in energy?
(c) What is the impact parameter at which the scattering angle is `90^@` for Z=79 and initial energy=10MeV?
(d) Why is it that the mass of the nucleus does not enter the formula above, but its charge does?
(e) for a given energy of the projectile, does the scattering angle increase or decrease with decrease in impact parameter?
View SolutionEvalute Rydberg constant by putting the value of the fundamental constants in its expression
View SolutionCalculate the value of 'fine structure constant'
View SolutionWhat is the angular momentum of an electon in the third orbit of an atom ?
View SolutionWrite down the expression for the radii of orbits of hydrogen atom. Calculate the radius of the smallest orbit
View SolutionCalculate the velocity of electron in Bohr's first orbit of hydrogen atom. How many times does the electron go in Bohr's first orbit in one second ?
View SolutionDetermine the speed of the electron in `n=3` orbit of `He^(+)` ion.
View SolutionShow that the speed of an electron in the innermost orbit of H-atom is 1/137 times the speed of light in vaccum.
View SolutionCalculate the period of revolution of an electron revolving in the first orbit of hydrogen atom. Given radius of first orbit `= 0.53 Å` and `c = 3 xx 10^(8) " ms"^(-1)`
View SolutionThe energy of an electron in the nth orbit is given by `E_(n)=-13.6//n^(2) eV`. Calculate the energy required to excite an electron from ground state to the second excited state.
View SolutionThe total energy of an electron in the first excited state of hydrogen atom is -3.4 eV.
(a) What is kinetic energy of electron in this state?
(ii) What is potential energy of electron in this state?
(c) Which of the answers above would change if the choice of zero of potential energy is changed?
View SolutionThe electron, in a given Bohr orbit has a total energy of `-1.5 eV`. Calculate its (i) kinetic energy, (ii) potential energy and (iii) the wavelength of light emitted, when the electron makes a transition to the ground state. Ground state energy `=-13.6 eV`
View SolutionThe energy levels of an atom of element X are shown in Fig. 20.2. Which one of the level transitions will result in the emission of photons of wavelength 620 nm ? Support your answer with mathematical calculations.
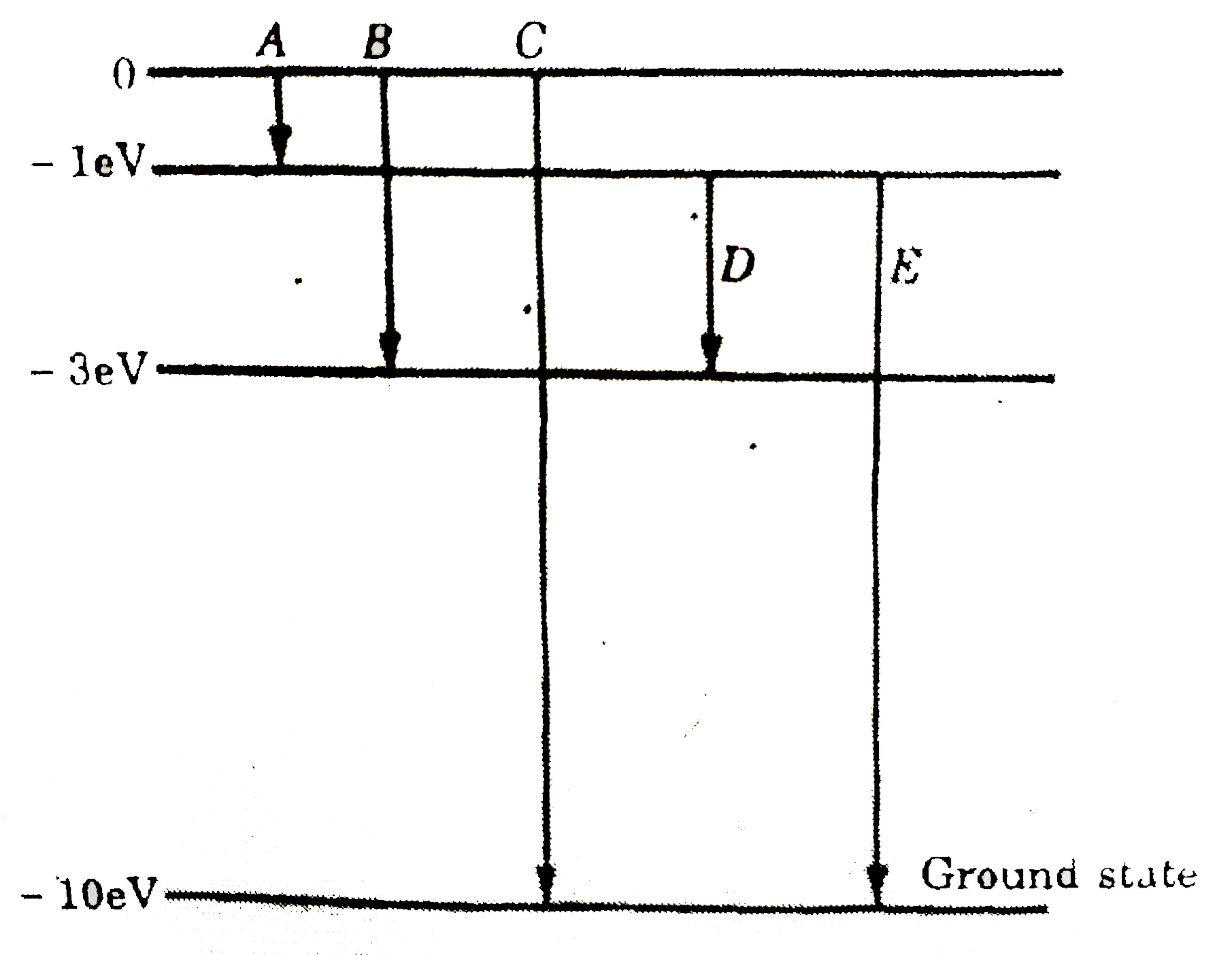
View SolutionUsing the Rydberg formula, calculate the wavelength of the first four spectral lines in the Lyman series of the hydrogen spectrum.
View SolutionCalculate the shortest and the longest wavelength of Lyman series. Given Ryberg's constant, `R = 10967700 " m"^(-1)`.
View SolutionThe wavelength of `H_(alpha)`, line of the Balmer series is `6553 Å`. Calculate the value of Ryberg constant.
View SolutionThe seond line of Balmer series has wavelength `4861 Å` The wavelength o fthe first line Balmer series is
View SolutionThe energy of an electron in an excited hydrogen atom is `- 3.4 e V`. Calculate the angular momentum . Given : Rydbrg's `R = 1.09737 xx 10^(-7) m^(-1)`. Plank's constant `h = 6.626176 xx 10^(-34) J - s`, speed of light`c = 3 xx 10^(8) m s^(-1).
View SolutionWhich state of triply ionised Beryllium `(Be^(+++))` the same orbital radius as that of the ground state hydrogen ?
View SolutionWhich level of the doubly ionized lithium has the same energy as the ground state energy of the hydrogen atom? Compare the orbital radii of the two levels.
View SolutionObtain the first Bohr radius and the ground state energy of a muonic hydrogen atom (i.e., an atom in which a negatively charged muon `(mu)` of mass about `207m_e` revolves around a proton).
View SolutionUsing Bohr's formula for energy quantization, determine (i) the longest wavelength in Lyman series of hydrogen atom spectrum. (ii) the excitation energy of the n=3 level of `He^(+)` atom. (iii) the ionization potential of the ground state of `Li^(++)` atom.
View SolutionObtain an expression for the frequency of radiations emitted when a hydrogen atom de-excites from level n to level (n-1). for larger n, show that the frequency equals the classical frequency of revolution of the electron in the orbit.
View SolutionA free electron of energy `1.4 eV` collides with a `H^(+)` ions. As a result of collision, a hydrogen atom in the ground state is formed and a photon is released. What is the wavelength of the emitted radiation ? In which part of the electromagnetic spectrum does this spectrum lie ? Give ionisation potential of hydrogen `=13.6 eV`
View SolutionExpress 16 mg mass into equivalent energy in eV.
View SolutionHow many electron- volt make one joule?
View SolutionExpress 1 joule in eV. Taking 1a.m.u. `=931 MeV`, calculate the mass of `._6C^12`.
View SolutionThe three stable isotopes of neon `._10Ne^(20), ._10Ne^(21)` and `._10Ne^(22)` have respective abundances of `90.51%,0.27%` and `9.22%`. The atomic masses of the three isotopes are `19.99u, 20.99u` and `21.99u` respectively. Obtain the average atomic mass of neon.
View SolutionThe natural boron is composed of two isotopes `._5B^10` and `._5B^11` having masses `10.003 u` and `11.009 u` resp. Find the relative abundance of each isotope in the natural boron if atomic mass of natural boron is 10.81u.
View SolutionCompare the radii of two nuclei with mass number 1 and 27 respectively.
View SolutionObtain approximately the ratio of the nuclear radii of the gold isotope `._(79)Au^(197)` and the silver isotope `._(47)Ag^(107)`. What is the approximate ratio of their nuclear mass densities ?
View SolutionThe nuclear mass of `._26F^(56)` is 55.85u. Calculate its nuclear density.
View SolutionWhy is nuclear density same for all nuclei?
View SolutionAssuming that protons and neutrons have equal masses, calculate how many times nuclear matter is denser than water. Take mass of a nucleon `=1.67xx10^(-27)kg and R_(0)=1.2xx10^(-15)m`.
View SolutionCalculate the binding energy if an `alpha`-particle in MeV Given : `m_(p)` (mass of proton) = 1.007825 amu, `m_(n)` (mass of neutron) = 1.008665 amu Mass of the nucleus `=4.002800 amu, 1 amu = 931 MeV.
View SolutionCalculate the binding energy per nucleon in the nuclei of `._(15)P^(31)`. Given `m(._(15)P^(31))=30.97376u, m(._(0)n^(1))=1.00865 u, m(._(1)H^(1))=1.00782u`.
View SolutionCalculate the binding energy per nucleon (B.E./nucleon) in the nuclei of `._(26)Fe^(56)`. Given :
`mp[._(26)Fe^(56)]=55.934939 " amu",m[._(0)n^(1)]=1.00865 " amu" , m[._(1)"II"^(1)]=1.00782 " amu"`
View SolutionCalculate binding energy per nucleon of `._(83)Bi^(209)`. Given :
`m(._(83)Bi^(209))=208.980388 " amu", m("neutron")=1.008665 " amu",m("proton") =1.007825 " amu"`.
View SolutionThe neutron separation energy is defined to be the energy required to remove a neutron form nucleus. Obtain the neutron separation energy of the nuclei `._(20)Ca^(41)` and `._(13)Al^(27)` from the following data : `m(._20Ca^(40))=39.962591u` and `m(._(20)Ca^(41))=40.962278u`
`m(._(13)Al^(26))=25.986895u` and `m(._(13)Al^(27))=26.981541u`
View SolutionWhat are alpha prticles ? In the reaction :
`._(Z)X^(A)rarr alpha+Y`
give the atomic number of Y.
View SolutionAn isotope `._(92)U^(238)` decays successively to form `._(90)Th^(234),._(91)Pa^(234),._(92)Th^(234),._(90)Th^(230)` and `._(88)Ra^(226)`. What are the radiations emitted in these five steps?
View SolutionWill neutron to proton ratio increase or decreases, when a radioactive nucleus emits (i) an alpha particle (ii) a beta particle ? Giveone example for each in support of your answer.
View SolutionThorium isotope `._(90)Th^(232)` emits some `alpha`-particle and some `beta`-particle and gets transformed into lead isotope `._(82)Pb^(200)`. Find the number of `alpha`-and `beta`-particles emitted.
View SolutionHalf-life of a certain radioactive materal against `alpha`-decay is 138 days. After what lapse of time the undecayed fraction of the material will be 6.25 % ?
View SolutionThe half-life period of a radioactive substance is 30 days. What is the time taken for 3/4 the of its original masss to disintegrate ?
View SolutionWhat `%` age of a given mass of a radioactive substance will be left undecayed after five half life periods?
View SolutionCalculate the half life period of a radioactive substance if its activity drops to `1/16` th of its initial value in 30 years.
View SolutionThe half-life of radium is 1600 years. After how many years 25 % of a radium block remains undecayed ?
View SolutionThe half-life of radon is 3.8 days. Calculate how much radon will be left out of 25 mg after 19 days.
View Solution1 mg radium has `2.68 xx 10^(18)` atoms. Its half-life is 1620 years. How many radium atoms will disintegrate from 1 mg of pure radium in 3240 years ?
View SolutionA certain radioactive substance has a half-life period of 30 days. What is the disintegration constant ?
View SolutionThe half-life of radium is 1500 years. After how many years will one gram of the pure radium
(i) reduce to one centigram ?
(ii) lose one milligram ?
View SolutionThe half life of radon is 3.8 days . After how many days will only one twentieth of radon sample be left over ?
View SolutionThe half -life of a radioactive substance is `1.192 xx 10^(7)`s against `alpha-`decay. Calculate the decay rate for `3.18 xx 10^(15)` atoms of the substance
View SolutionCalculate the number of disintegrations per second of 1 g of a radioactive sample whose half-life is `1.4 xx 10^(16)s`. The mass number of the sample is 238
View SolutionDetermine the amount of `._84Po^(210)` necessary to provide a source of `alpha` particles of 5 millicurie strength. The half life of Po is 138 days.
View SolutionThe atomic weight of radius is 226. It is observed that `3.67 xx 10^(10) " " alpha-`particles are emitted per second from one gram of radium. Calculate in years the half period of radium.
View SolutionThe half-life of `^198 Au` is `2.7 days`. Calculate (a) the decay constant, (b) the average-life and (C ) the activity of `1.00 mg` of `^198 Au`. Take atomic weight of `^198 Au` to be `198 g mol^(-1)`.
View SolutionThe normal activity of living carbon -containing matter is found to be about 15 decay per minute for every gram of carbon. This activity arises form the small proportion of radioactive `._6C^(14)` present with the ordinary `._6C^(12)` isotope. When the organism is dead, its interaction with the atmosphere which maintains the above equilibrium activity, ceases and its activity begins to drop. from the known half life (=5730years) of `._6C^(14)`, and the measured activity, the age of the specimen can be approximately estimated. This is the principle of `._6C^(14)` dating used in archaeology. Suppose a specimen from Mohenjo - daro gives an activity of 9 decays per minute per gram of carbon. Estimate the approximate age of the Indus Valley Civilization.
View SolutionThere is a stream of neutrons with kinetic energy of 0.0327 eV. If half life of neutrons is 700s, what fraction of neutrons will decay before they travel a distance of 10m? Take mass of neutron =`1.675xx10^(-27)kg.`
View SolutionThe nucleus `._(92)U^(238)` is unstable angainst alpha decay with half-life of `4.5 xx 10^(9)` years. Estimate the kinetic energy of the emitted `alpha`-particle.
Mass of the `._(92)U^(238)` atom `= 238.05081 u`
Mass of the `._(2)He^(4)` atom `= 4.00260 u`
Mass of the `._(90)Th^(234)` atom `= 234.04363 u`
View SolutionThe nucleus `.^(23)Ne` deacays by `beta`-emission into the nucleus `.^(23)Na`. Write down the `beta`-decay equation and determine the maximum kinetic energy of the electrons emitted. Given,`(m(._(11)^(23)Ne) =22.994466 am u` and `m (._(11)^(23)Na =22.989770 am u`. Ignore the mass of antineuttino `(bar(v))`.
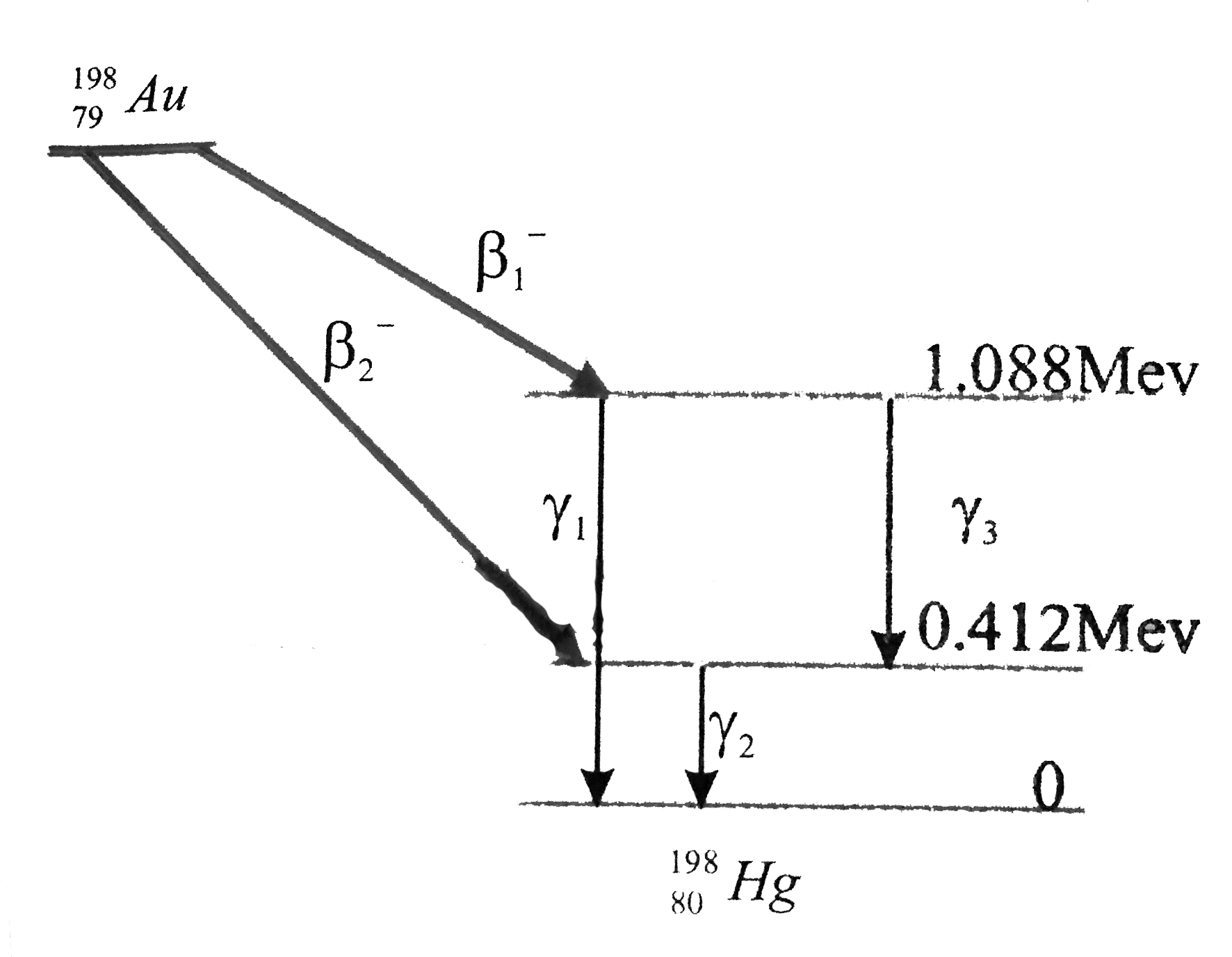
View SolutionObtain the maximum kinetic energy of `beta`-particles, and the radiation frequencies of `gamma` decays in the decay scheme shown in Fig. `14.6`. You are given that `m(.^(198)Au)=197.968233 u, m(.^(198)Hg)=197.966760 u`
View SolutionA neutron is absorbed by a `._3Li^6` nucleus with subsequent emission of an alpha particle. Write the corresponding nuclear reaction. Calculate the energy released in this reaction.
`m(._3Li^6)=6.015126u, m(._2He^4)=4.0026044u`
`m(._0n^1)=1.0086654u, m(._1He^3)=3.016049u`
Take `1u=931MeV`.
View SolutionThe Q value of a nuclear reaction
A+b=C+d is defined by `Q=[m_A+m_b-m_C-m_d]c^2` where the masses refer to the respective nuclei. Determine form the given data the Q value of the following reactions and state whether the reactions are exothermic of endothermic.
(i) `._1H^(1)+._1H^3to ._1H^2+._1H^2`
(ii) `._6C^(12)+._6C^(12) to ._10Ne^(20)+._2He^4`
Atomic masses are given to be
`m(._1H^2)=2.014102u , m(._1H^3)=3.016049 u, m(._6C^(12))=12.000000u , m(._10Ne^(20))=19.992439u`
View SolutionConsider one of the fission reactions of `U^(235)` by thernmal neutrons :
`._(92)U^(235) + n rarr ._(38)Sr^(94) + ._(54)Ce^(140) + 2n`
The fission fragments are, however, not stable. They unaergo successive `beta-`decays unit `._(38)Sr^(94)` becomes `._(40)Zr^(94)` and `._(54)Xe^(140)` becomes `._(58)Ce^(140)`. Estimate the total energy released in the process. Is all that energy available as kinetic energy of the fission products (Zr and Ce)? You are given that
`m (U^(235)) = 255.0439 am u," " m_(n) = 1.00866 am u " " m(Zr^(94)) = 93.9065 am u, " " m(Ce^(140)) = 139.9055 am u`
View SolutionIf `200 MeV` energy is released in the fission of a single `U^235` nucleus, the number of fissions required per second to produce `1` kilowatt power shall be (Given `1 eV = 1.6 xx 10^-19 J`).
View SolutionCalculate the energy released by fission from `2 g` of `.^(235)._(92)U` in `kWh`. Given that the energy released per fission is `200 MeV`.
View SolutionIt is estimated that the atomic bomb exploded at Hiroshima released a total energy of `7.6xx10^(13)J`. If on the average, 200MeV energy was released per fission, calculate
(i) the number of Uranium atoms fissioned,
(ii) the mass of Uranium used in the bomb.
View SolutionSuppose India has a target of producing by 2000 A.D., 100,000 MW of electric power , 10 percent of which is to be obtained from nuclear power plants. Suppose we are given that, on average the efficiency of utilisation (i.e., conversion to electric energy) of thermal energy porduced in a reactor is `25 %`. How much amount of fissionable uranium would our country need per year at the turn of this century ? Take the heat energy per fission of `U^(235)` to be about 200 MeV. Avogadro's Number `N = 6.023 xx 10^(23) mol^(-1)`.
View SolutionWhat is the power output of a `._(92) U^(235)` reactor if it is takes `30` days to use up `2 kg` of fuel, and if each fission gives `185 MeV` of usable energy ?.
View SolutionIn a star, three alpha particle join in a single reaction to form `._(6)C^(12)` nucleus. Calcuate the energy released in the reaction
Given : `m(._(2)He^(4)) = 4.002604 am u, " " m(._(6)C^(12)) = 12.000000 am u`
View SolutionAssuming that four hydrogen atom combine to form a helium atom and two positrons, each of mass `0.00549u`, calculate the energy released. Given `m(._(1)H^(1))=1.007825u, m(._(2)He^(4))=4.002604u`.
View SolutionIt is proposed to use the nuclear fusion reaction,
`._1^2H+_1^2Hrarr_2^4He`
in a nuclear reactor `200 MW` rating. If the energy from the above reaction is used with a `25` per cent efficiency in the reactor, how many grams of deuterium fuel will be needed per day?(The masses of `._1^2H` and `._2^4He` are `2.0141` atomic mass units and `4.0026` atomic mass units respectively.)
View SolutionConsider the so called D-T reaction (deuterium-tritium fusion) `._1H^2+._1H^3to._2He^4+n`
Calculate the energy released in MeV in this reaction from the data
`m(._1H^2)=2.014102u, m(._1H^3)=3.016049u`
(b) Consider the radius of both deuterium and tritium to be approximately 2.0fm. what is the kinetic energy needed to overcome the Coulomb repulsion between the two nuclei? To what temperature must the gases the be heated to initiate the reaction?
View Solution
Example questions and complete solutions for chapter ATOMS, NUCLEI AND MOLECULES of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 12