Complete Solutions to Problem of chapter ATOMS, NUCLEI AND MOLECULES of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ATOMS, NUCLEI AND MOLECULES |
| SL ARORA | Problem |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
Calculate the nearest distance of approach of an `alpha`-particle of energy 2.5 Me V being scattered by a gold nucleus (Z=79).
View SolutionSuppose the potential energy between an electron and aproton at a distance `r` is given by `-Ke^(2)// 3 r^(3)`. Use Bohr's theory to obtain energy level of such a hypothetical atom.
View SolutionA single electron orbits a stationary nucleus of charge `+ Ze`, where `Z` is a constant and `e` is the magnitude of electronic charge . It requires `47.2 eV` to excite . Find
a the value of `Z`
b the energy required to excite the electron from the third to the fourth Bohr orbit.
the wavelength of electromagnetic rediation required to remove the electron from the first Bohr orbit to infinity.
d Find the `KE,PE`, and angular momentum of electron in the first Bohr orbit.
the redius of the first Bohr orbit
[The ionization energy of hydrogen atom `= 13.6 eV` Bohr radius `= 5.3 xx 10^(_11) m`, "velocity of light" `= 3 xx 10^(-8)jm s ^(-1)`, Planck's constant `= 6.6 xx 10^(-34)j - s]`
View SolutionAn electron , in a hydrogen-like atom, is in excited state. It has a total energy of -3.4 eV. Calculate
(a) the kinetic energy and
(b) the de Broglie wavelength of the electron.
View SolutionHow many revolutions does an electron in the first orbit of hydrogen atom make per second ? Calculate the orbital frequency. Given `h = 6.6 xx 10^(-34) Js, " " m_(e) = 9.1 xx 10^(-31) kg, " " r_(0) = 0.53 Å`
View SolutionAn electron moves about a proton in a circular orbit of radius `5 xx 10^(-11)m`. (i) find the orbital angular momentum of the electron about the proton (ii) Express total energy in electron volt.
View SolutionUsing Bohr's formula for energy quantisation, determine (i) the largest wavelength in Balmer series of hydrogen atom spectrum and (ii) the excitation energy of `n = 3` level of `He^(+)` ion. Given `R = 1.097 xx 10^(7) m^(-1)`
View SolutionSuppose a moving hydrogen atmo makes a head on inelastic collision with a stationary hydrogen atmo. Before collision both atoms are in ground state and after collision they move together. What is the minimum velocity of the moving hydrogen atom if one of the atom is to be given the minimum excitation energy after the collision ? `(m_(H) = 1.0078 am u, 1 am u = 1.66 xx 10^(-27) kg)`
View SolutionHydrogen atom in its ground state is excited by means of monochromatic radiation of wavelength `970.6 Å`. How many lines are possible in the resulting emission spectrum ? Calculate the longest wavelength amongst them. You may assume that the ionisation energy for hydrogen atom is 13.6 eV. Given Planck's constant `= 6.6 xx 10^(-34)Js, " " c = 3 xx 10(8) ms^(-1)`
View SolutionA double ionised lithium atom is hydrogen like with atomic number `3`
(i)Find the wavelength of the radiation to excite the electron in `Li^(++)`from the first to the third bohr orbit (lonisation energy of the hydrogen atom equals `13. 6eV`
(ii) How many spectral lines are observed in the emission spectrum of the above excited system ?
View SolutionA gas of hydrogen - like ion is perpendicular in such a way that ions are only in the ground state and the first excite state. A monochromatic light of wavelength `1216 Å` is absorved by the ions. The ions are lifted to higher excited state and emit emit radiation of six wavelength , some higher and some lower than the incident wavelength. Find the principal quantum number of the excited state identify the nuclear charge on the ions . Calculate the values of the maximum and minimum wavelengths.
View SolutionA hydrogen like atom (atomic number Z) is in a higher excited state of quantum number n. The excited atom can make a transition to the first excited state by successively emitting two photons of energy 10.2 eV and 17.0 eV, respectively. Alternatively, the atom from the same excited state can make a transition to the second excited state by successively emitting two photons of energies 4.25 eV and 5.95 eV, respectively Determine the values of n and Z. (lonization energy of H-atom = 13.6 eV)
View SolutionThe wavelength of the first line of Lyman series for hydrogen is identical to that of the second line of Balmer series for some hydrogen like ion x. Calculate energies of the first four levels of x.
View SolutionTwo hydrogen-like atoms `A` and `B` are of different masses and each atom contains equal numbers of protons and neutrons. The difference in the energies between the first Balmer lines emitted by `A and B` , is `5.667 e V`. When atom atoms `A and B` moving with the same velocity , strike a heavy target , they rebound with the same velocity in the process, atom `B` imparts twice the momentum to the target than that `A` imparts. Identify the atom `A and B`.
View SolutionThe stopping potential for the photo-electrons emitted from a metal surface of work-function 1.7 eV is 10.4 eV. Find the wavelength of the radiation used. Also identify the energy-levels in hydrogen atom which will emit this wavelength.
View SolutionLight form a dicharge tube containing hydrogen atoms falls on the surface of a piece of sodium. The kinetic energy of the fastest photoelectrons emitted from sodium is 0.73 eV. The work function for sodium is 1.82 eV. Find (a) the energy of the photons causing the photoelectrons emission.
(b) the quantum numbers of the two levels involved in the emission of these photons.
(c ) the change in the angular momentum of the electron in the hydrogen atom, in the above transition, and
(d) the recoil speed of the emitting atom assuming it to be at rest before the transition. (lonization potential of hydrogen is 13.6 eV.)
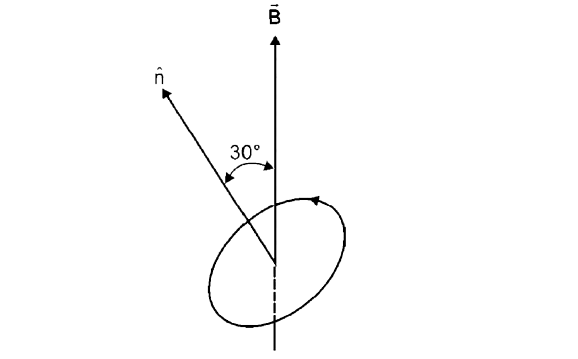
View SolutionAn electron in the ground state of hydrogen atom is revolving in anticlock-wise direction in a circular orbit of radius `R`.
(i) Obtain an experssion for the orbital magnetic dipole moment of the electron.
(ii) The atom is placed in a uniform magnetic induction `vec(B)` such that the plane - normal of the electron - orbit makes an angle of ` 30^(@)` with the magnetic induction . Find the torque experienced by the orbiting electron.
View SolutionA sample contains `10^(-2)kg` each of two substances A and B with half lives 4 sec and 8 sec respectively. Their atomic weights are in the ratio `1:2`. Find the amounts of A and B after an interval of 16 seconds.
View SolutionThe disintegration rate of a certain radioactive sample at any instant is `4750` disintegrations per minute. Five minutes later the rate becomes `2700` per minute. Calculate
(a) decay constant and (b) half-life of the sample
View SolutionAt a given instant there are `25%` undecayed radioactive nuclei in a sample. After `10 s` the number of undecayed nuclei reduces to `12.5%`. Calculate
(a) mean life of the nuclei,
(b) the time in which the number of undecayed nuclei will further reduce to` 6.25%` of the reduced number.
View SolutionThe isotope of `U^(238) and U^(235)` occur in nature in the ratio `140:1`. Assuming that at the time of earth's formation, they were present in equal ratio, make an estimate of the age of earth. The half lives of `U^(238)` and `U^(235)` are `4.5xx10^9` years and `7.13xx10^8` years respectively. Given `log_(10)140=2.1461 and log_(10)2=0.3010.`
View SolutionThe mean lives of a radioactive substance are 1620 years and 405 years for `alpha` emission and `beta` emission respectively. Find out the time during which three fourth of a sample will decay if it is decaying both by `alpha`-emission and `beta`-emission simultaneously. `(log_e4=1.386).`
View SolutionSome amount of a radioactive substance (half-life= 10 days) is spread inside a room and consequently the level of radiation becomes 50 times the permissible level for normal occupancy of the room. After how many days the room will be safe for occupation?
View SolutionA small quantity of solution containing `Na^(24)` radio nuclide (half-life 15 hours) of activity 1.0 microcurie is injected into the blood of a person. A sample of the blood of volume `1 cm^(2)` taken after 5 hours shows an activity of 296 disintegrations per minute. Determine the total volume of blood in the body of the person. (1 curie `=3.7xx10^(10)` disintegrations per second.)
View SolutionIn the chemical analysis of a rock the mass ratio of two radioactive isotopes is found to be `100:1`. The mean lives of the two isotopes are `4xx10^9` years and `2xx10^9` years, respectively. If it is assumed that at the time of formation the atoms of both the isotopes were in equal propotional, calculate the age of the rock. Ratio of the atomic weights of the two isotopes is `1.02:1`.
View SolutionA sample of uranium is a mixture of three isotopes `._(92)U^(234), ._(92)U^(235)` and `._(92)U^(238)` present in the ratio `0.006%, 0.71%` and `99.284%` respectively. The half lives of then isotopes are `2.5xx10^(5)` years, `7.1xx10^(8)` years and `4.5xx10^(9)` years respectively. The contribution to activity (in `%`) of each isotope in the sample respectively
View Solution`10^(-3) kg` of a radioactive isotope (atomic mass 226) emits `3.72xx10^(10) alpha`- particles in a second. Calculate the half-life of the isotope. If `4.2xx10^(2)` joule energy is released in one hour in this process what is the average energy of the `alpha`-particles? Avogadro number is `6.02xx10^(26)//` kmol and `log_(e)2 =0.693`.
View SolutionNuclei of radioactive element A are being produced at a constant rate. `alpha`. The element has a decay constant `lambda`. At time `t=0`, there are`N_(0)` nuclei of the element.
(a) Calculate the number N of nuclei of A at time t.
(b) IF `alpha =2 N_(0) lambda` , calculate the number of nuclei of A after one half-life time of A and also the limiting value of N at `t rarr oo`.
View SolutionThe element curium `._96^248 Cm` has a mean life of `10^13s`. Its primary decay modes are spontaneous fission and `alpha`-decay, the former with a probability of `8%` and the later with a probability of `92%`, each fission releases `200 MeV` of energy. The masses involved in decay are as follows
`._96^248 Cm=248.072220 u`,
`._94^244 P_u=244.064100 u` and `._2^4 He=4.002603u`. Calculate the power output from a sample of `10^20` Cm atoms. (`1u=931 MeV//c^2`)
View SolutionA nuclear reactor generates power at 50% efficiency by fission of `._(92)^(235)U` into two equal fragments of `._(46)^(116)U` into two equal fragments of `._(46)^(116)Pd` with the emission of two gamma rays of 5.2 MeV each and three neutrons. The average binding energies per particle of `._(92)^(235)U` and `._(46)^(116)Pd` are 7.2 MeV and 8.2MeV respectiveley. Calculate the energy released in one fission event. Also-estimate the amount to `.^(235)U` consumed per hour to produce 1600 megawatt power.
View SolutionA star initially has `10^(40) ` deuterons. It produces energy via the process `_(1)H^(2) + _(1)H^(2) + rarr _(1) H^(3) + p. `and `_(1)H^(2) + _(1)H^(3) + rarr _(2) He^(4) + n` .If the average power radiated by the state is `10^(16) W` , the deuteron supply of the star is exhausted in a time of the order of .
The masses of the nuclei are as follows:
`M(H^(2)) = 2.014 amu,`
`M(p) = 1.007 amu, M(n) = 1.008 amu, M(He^(4)) = 4.001 amu`.
View SolutionA fusion reaction of the type given below
`._(1)^(2)D+._(1)^(2)D rarr ._(1)^(3)T+._(1)^(1)p+DeltaE`
is most promissing for the production of power. Here D and T stand for deuterium and tritium, respectively. Calculate the mass of deuterium required per day for a power output of `10^(9) W`. Assume the efficiency of the process to be `50%`.
Given : `" "m(._(1)^(2)D)=2.01458 am u," "m(._(1)^(3)T)=3.01605 am u`
`m(._(1)^(1) p)=1.00728 am u` and `1 am u=930 MeV`.
View Solution
Problem questions and complete solutions for chapter ATOMS, NUCLEI AND MOLECULES of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 12