Complete Solutions to EXAMPLE of chapter வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் |
| SURA PUBLICATION(TAMIL) | EXAMPLE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
`veca` மற்றும் `vecb` என்பன இணைவெக்டர்கள் எனில், `[vecavecbvecc]`-ன் மதிப்பு காண்க.
02:23View Solution`beta` மற்றும் `vecr`ஆகியவை அமைக்கும் தளத்தில் `vecalpha` அமைந்துள்ளது எனில்,
01:45View Solution`veca.vecb=vecb.vecc=vecc.veca=0` எனில் `[veca,vecb,vecc]`-ன் மதிப்பு
02:08View Solution`veca-க்கு செங்குத்தாகவும் `vecc`-க்கு இணையாகவும் உள்ள வெக்டர் `veca` என்றவாறுள்ள ஓரலகு வெக்டர்கள் `veca,vecb,vecc` எனில், `vecaxx(vecbxxvecc)`-க்குச் சமமானது.
View Solution`[veca,vecb,vecc]=1` எனில், `frac{veca.(vecbxxvecc)}{(veccxxveca).vecb}+frac{vecb.(veccxxveca)}{(vecaxxvecb).vecc}+frac{vecc.(vecaxxvecb)}{(veccxxvecb).veca`-ன் மதிப்பு
04:33View Solution`hati + hatj, hati + 2hatj, hati+hatj+pihatk` என்ற வெக்டர்களை ஒரு புள்ளியில் சந்திக்கும் விளிம்புகளாகக் கொண்ட இணைகரத் திண்மத்தின் கன அளவு
01:51View Solution`veca,vecb` என்பன `[veca,vecb,vecaxxvecb]=pi/4` எனுமாறுள்ள ஓரலகு வெக்டர்கள் எனில், `veca` மற்றும் `vecb` ஆகியவற்றுக்க இடைப்பட்ட கோணம்.
05:37View Solution`veca=hati+hatj+hatk, vecb=hati+hatj,vecc=hati` மற்றும் `(vecaxxvecb)xxvecc=lambdaveca+muvecb` எனில், `lambda+mu`-ன் மதிப்பு
03:02View Solution`veca,vecb,vecc` என்பன `[veca,vecb,vecc]=3` எனமாறுள்ள ஒரு தளம் அமையா மூன்று பூச்சியமற்ற வெக்டர்கள் எனில், `{[[vecaxxvecb,vecbxxvecc,veccxxveca]]}^2`-ன் மதிப்பு
01:49View Solution`veca,vecb,vecc` என்பன `vecaxx(vecbxxvecc)=frac{vecb+vecc}{sqrt2}` எனுமாறுள்ள ஒரு தளம் அமையா மூன்று வெக்டர்கள் எனில், `veca` மற்றும் `vecb` ஆகியவற்றுக்கு இடைப்பட்ட கோணம்.
04:46View Solution`vecaxxvecb,vecbxxvecc,veccxxveca` ஆகியவற்றை ஒரு புள்ளியில் சந்திக்கும் விளிம்புகளாகக் கொண்ட இணைகரத் திண்மத்தின் கன அளவு 8 கன அலகுகள் எனில், `(vecaxxvecb)xx(vecbxxvecc),(vecbxxvecc)xx(veccxxveca)` மற்றும் `(veccxxveca)xx(vecaxxvecb)` ஆகியவற்றை ஒரு புள்ளியில் சந்திக்கும் விளிம்புகளாகக் கொண்ட இணைகரத் திண்மத்தி்ன கன அளவு
03:58View Solution`veca,vecb,vecc,vecd` என்பன `(vecaxxvecb)xx(veccxxvecd)=vec0` எனமாறுள்ள வெக்டர்கள் என்க. `veca,vecb` என்ற ஒரு ஜோடி வெக்டர்களாலும் மற்றும் `vecc,vecd` என்ற ஜோடி வெக்டர்களாலும் அமைக்கப்படும் தளங்கள் முறையே `P_1`மற்றும் `P_2` எனில், இத்தளங்களுக்க இடைப்பட்ட காேணம்.
02:30View Solution`veca,vecb,vecc` என்பன `vecb.veccne0` மற்றும் `veca.vecbne0` எனமாறுள்ள மூன்று வெக்டர்கள் என்க. `vecaxx(vecbxxvecc)=(vecaxxvecb)xxvecc` எனில், `veca` மற்றும் `vecc` என்பவை
03:07View Solution`veca=2hati+3hatj-hatk,vecb=hati+2hatj-5hatk,vecc=3hati+5hatj-hatk` எனில், `veca`-க்குச் செங்குத்தாகவும் `vecb` மற்றும் `vecc` என்ற வெக்டர்கள் உருவாக்கும் தளத்தி்ல் அமைவதுமான வெக்டர்.
05:42View Solution`frac{x-2}{3}=frac{y+1}{-2},z=2` மற்றும் `frac{x-1}{1}=frac{2y+3}{3},frac{z+5}{2}` என்ற கோடுகளுக்கு இடைப்பட்ட கோணம்.
04:35View Solution`frac{x-2}{3}=frac{y-1}{-5}=frac{z+2}{2}` என்ற கோடு `x+3y-alphaz+beta=0` என்ற தளத்தின் மீது இருந்தால், பின்னர் `(alpha,beta)` என்பது
06:16View Solution`vecr=(hati+2hatj-3hatk)+t(2hati+hatj-2hatk)` என்ற கோட்டிற்கும் `r.(hati+hatj)+4=0` என்ற தளத்திற்கும் இடைப்பட்ட கோணம்
02:32View Solution`vecr=(6hati-hatj-3hatk)+t(-hati+4hatk)` என்ற கோடு `vecr.(hati+hatj-hatk)=3` என்ற தளத்தை சந்திக்கும் புள்ளியின் அச்சுத்தூரங்கள்.
05:14View Solutionஆதிப்புள்ளியிலிருந்து 3x-6y+2z+7=0 என்ற தளத்திற்கு உள்ள தொலைவு
01:40View Solutionx+2y+3z+7=0 மற்றும் 2x+4y+6z+7=0 ஆகிய தளங்களுக்கு இடைப்பட்ட தொலைவு
03:44View Solutionஒரு கோட்டின் திசைக் கொசைன்கள் 1/c, 1/c, 1/c எனில்,
01:22View Solution`vecr=(hati-2hatj-hatk)+t(6hati-hatk)` என்ற வெக்டர் சமன்பாடு குறிக்கும் நேர்க்கோட்டின் மீது உள்ள புள்ளிகள்.
02:42View Solutionஆதியிலிருந்து (1, 1, 1) என்ற புள்ளிக்கு உள்ள தொலைவானது x+y+z+k=0 என்ற தளத்திலிருந்து அப்புள்ளிக்கு உள்ள தொலைவில் பாதி எனில், k-ன் மதிப்புகள்
04:53View Solution`vecr.(2hati-lambdahatj+hatk)=3` மற்றும் `vecr.(4hati+hatj-muhatk)=5` ஆகிய தளங்கள் இணை எனில், `lambda` மற்றும் `mu`-ன் மதிப்புகள்
03:16View Solutionஆதியிலிருந்து `2x+3y+lambdaz=1, lambda>0` என்ற தளத்திற்கு வரையப்படும் செங்குத்தின் நீம் 1/5 எனில், `lambda`-ன் மதிப்பு
03:03View Solution`lambdahati+hatj+2hatk,hati+lambdahatj-hatk` மற்றும் `2hati-hatj+lambdahatk` வெக்டர்கள் ஒரு தளம் அமைவன எனில்,
06:14View Solution`veca,vecb,vecc` என்பது மூன்று ஒரு தளம் அமையா வெக்டர்கள் மற்றும் `vecp,vecq,vecr` வெக்டர்கள் வரையறுக்கப்படும் தொடர்புகள் `vecp=frac{vecbxxvecc}{[vecavecbvecc]},vecq=frac{veccxxveca}{[vecavecbvecc]},vecr=frac{vecaxxvecb}{[vecavecbvecc]}` பிறகு மதிப்பு `(veca+vecb).vecp+(vecb+vecc).q+(vecc+veca).vecr` =
04:02View Solution`(hati+hatj)` மற்றும் `(hatj+hatk)` வெக்டர்களின் செங்குத்து வெக்டர்களின் எண்ணிக்கை
02:22View Solution`vecd=vecaxx(vecbxxvecc)+vecbxx(veccxxveca)+veccxx(veca+vecb)` எனில்,
03:40View Solution`veca`மற்றும் `vecb` அலகு வெக்டர் எனில், `(veca+vecb)xx(vecaxxvecb)`-க்கு இணையான வெக்டரானது
03:52View Solution`veca=3hati+hatj-2hatk` மற்றும் `vecb=hati-3hatj+4hatk` வை மூலைவிட்டங்களாக கொண்ட இணைகரத்தின் பரப்பு
04:45View Solution`veca,vecb`மற்றும் `vecc` ஏதேனும் மூன்று வெக்டர்கள் எனில், `(vecaxxvecb)xxvecc=vecaxx(vecbxxvecc)` மட்டும்
03:07View Solution`overlineOA=2hati-3hatj, overlineOB=hati+hatj-hatk` மற்றும் `overlineOC=3hati-hatk` -யை பக்கங்களாக கொண்ட திண்ம இணைகரத்தின் கனஅளவு காண்க.
02:52View Solution`|veca|=|vecb|=1` எனுமாறு `veca+2vecb` மற்றும் `5veca-4vecb` ஒன்றுக்கொன்று செங்குத்து எனில் `veca`மற்றும் `vecb`-க்கு இடையேயான கோணம்
04:18View Solution`3hati+4hatj+5hatk` மற்றும் Z-அச்சுக்கு இடையேயான கோணம்.
03:16View Solutionஒரு வெக்டர் `vecOP` ஆனது x மற்றும் y அச்சுகளின் மிகைத் திசையில் முறையே `60^@` மற்றும் `45^@`-ஐ ஏற்படுத்துகின்றது. `vecOP` ஆனது z-அச்சுடன் ஏற்படுத்தும் கோணம்
08:38View Solution`veca=2hati+2hatj+3hatk,vecb=-hati+2hatj+hatk, vecc=3hati+hatj` பிறகு `veca+lamdavecb` ஆனது `vecc`-க்கு செங்குத்து எனில் lamda =
04:38View Solutionவெக்டர்கள் `veca`மற்றும் `vecb` க்கு இடையேயான கோணம் `theta` எனில் `sin ((theta)/2)` என்பது
View Solutionவெக்டர்கள் `hati+hatj+2hatk`,`-hati+2hatk` மற்றும்`2hati+xhatj-yhatk` ஒன்றுக்கொன்று செங்குத்து எனில் x, y, z - மதிப்புகள்
View Solution`veca=|veca|vece`எனில் `vece.vece` என்பது
01:32View Solution`|veca+vecb|^2+|veca-vecb|^2` என்பதன் மதிப்பு
02:32View Solution`vecpxxvecq=2hati+3hatj,vecrxxvecs=3hatj+2hatk`எனில் `vecp.(vecqxx(vecrxxvecs))`
03:38View Solution`vecF=hati+mj-hatk` என்ற விசை ஒரு துகளை (1, 1, 1) என்ற புள்ளியிலிருந்து (3, 3, 3) என்ற புள்ளிக்கு நகர்த்தும் பொழுது செய்யப்பட்ட வேலை 12 அலகுகள் எனில், m என்பது
03:43View Solution3x+3y-3z-1=0 மற்றும் x+y-z+5=0 என்ற இரண்டு தளங்கள்
03:55View Solutionநேர்க்கோடுகள் `frac{x-3}{2}=frac{y+5}{4}=frac{z-1}{-13}` மற்றும் `frac{x+1}{3}=frac{y-4}{5}=frac{z+2}{2}`என்பது
03:37View Solutionநேர்க்கோடுகள் `frac{x+2}{2}=frac{y}{-3}=frac{z-1}{4}` மற்றும் `frac{x-3}{a}=frac{y-1}{4}=frac{z-7}{a}` செங்குத்து எனில், `(veca)` -ன் மதிப்பு
02:55View Solution`[veca,vecb,vecc]=3`மற்றும் `|vecc|=1`எனில் `|(vecbxxvecc)xx(veccxxveca)|` என்பது
04:08View Solution`lambdahati+2lambdahatj+2lambdahatk` என்பது ஓரலகு வெக்டர் எனில், `lambda`-ன் மதிப்பு
05:39View Solution`veca,vecb` மற்றும் `vecc` ஏதேனும் மூன்று வெக்டர் `(veca+vecb).(vecb+vecc)xx(vecc+veca)`
02:32View Solution`ahati+hatj+hatk, hati+bhatj+hatk`மற்றும் `hati+hatj+chatk (anebnecne1)` ஒரு தள வெக்டர்கள் எனில் `frac{1}{1-a}+frac{1}{1-b}+frac{1}{1-c}` '
03:16View Solution2x+y-z=9 மற்றும் x+2y+z=7 தளங்களுக்கு இடையேயான கோணம் ------------
03:35View Solution2x+3y+4z=5 என்ற தளத்துக்கான ஓரலகு செங்குத்து வெக்டர் ------------
03:30View Solutionஒரு துகள் A(3, 3, 3) என்ற புள்ளியிலிருந்து B(4, 4, 4) என்ற புள்ளிக்கு `vecF=hati+hatj+hatk`என்ற விசையின் செயல்பாட்டினால் நகர்த்தப்பட்டால் அவ்விசை செய்த மொத்த வேலை -------------- அலகுகள்
03:04View Solutionகீழ்க்காணும் வெக்டர்களுக்கு இடைப்பட்ட கோணத்தைக் காண்க. `hati-hatj` மற்றும் `hatj-hatk`
10:05View Solutionதளம் 2x-y+2z=5-க்கு செங்குத்து அலகு வெக்டர்கள்-----------------
01:47View Solutionஆதியிலிருந்து தளம் `vecr.(2hati-hatj+5hatk)=7`-க்கான தூரம்----------
03:03View Solution`veca, vecb,vecc` ஒன்றுக்கொன்று செங்குத்து அலகு வெக்டர்கள் எனில், `|veca+vecb+vecc|` என்பது---------
02:50View Solution`vecu, vecv,vecw`எனுமாறு வெக்டர்கள் `vecu+vecv+vecw=vec0` என்க. `|vecu|=3,|vecv|=4, |vecw|=5` எனில், `vecu.vecv+vecv.vecw+vecw.vecu` என்பது-----------
03:49View Solutionஆதியிலிருந்து தளம் `vecr.(3hati+4hatj+12hatk)=26` -க்கான செங்குத்தின் நீளம்.----------------
03:18View Solution`|vecaxxvecb|=veca.vecb` எனில், வெக்டர்கள் `veca` மற்றும் `vecb`-க்கு இடையேயான கோணம் -------------
02:07View Solution`|a| = 1`எனில், `|vecaxxhati|^2+|vecaxxhatj|^2+|vecaxxhatk|^2`-ன் மதிப்பு ---------
05:07View Solution`veca.vecb.vecc` ஒரு தள வெக்டர்கள் இல்லையெனில் `frac{veca.(vecbxxvecc)}{(veccxxveca).vecb}+frac{vecb.(vecaxxvecc)}{vecc.(vecaxxvecb)}`=
04:29View Solution`vecd=lambda(vecaxxvecb)+mu(vecbxxvecc)+omega(veccxxveca)` மற்றும் `|veccxxveca|=1/8` எனில், `lambda+mu+omega`--------------
03:31View Solution`veca=3hati+hatj-2hatk` மற்றும் `vecb=hati-3hatj+4hatk` வை மூலைவிட்டங்களாக கொண்ட இணைகரத்தின் பரப்பு
04:45View Solutionஎண்ணளவுகள் முறையே 1, 1, 2 உடைய வெக்டர்கள் `veca, vecb` மற்றும் `vecc` என்க. `vecaxx(vecaxxvecc)+vecb=0` எனில், `veca` மற்றும் `vecc`-க்கு இடையேயான குறுங்கோணம்.------------------
04:52View Solutionபொருந்தாத ஒன்றை தேர்ந்தெடுக்க :
02:43View Solutionஎந்த ஒரு பூச்சியமற்ற வெக்டர்கள் `veca`மற்றும் `vecb` `vecaxxvecb` எனபது
01:37View Solutionஎந்த பூச்சியமற்ற வெக்டர்கள் `veca, vecb` மற்றும் `vecc` -க்கு `(vecaxxvecb).vecc` என்பது
03:27View Solution`veca,vecb` மற்றும் `vecc` ஒரு தள வெக்டர்கள் எனில்
02:43View Solutionஆதிப்புள்ளியிலிருந்து தளத்திற்கு உள்ள தூரம் p மற்றும் தளத்திற்குச் செங்குத்தான ஓரலகு. வெக்டர் `hatd` எனில், தளத்தின் சமன்பாடு
00:51View Solutionதவறான விடையை தேர்ந்தெடுக்க: `frac{x-6}{6}=frac{y+4}{4}=frac{z-4}{8}` என்ற கோட்டிற்கு
04:25View Solutionதவறான விடையை தேர்ந்தெடுக்க: தளம் `vecr.(2hati+3hatj+5hatk)=3` -க்கு
03:16View Solutionதவறான விடையை தேர்ந்தெடுக்க: புள்ளி `vecr=(hati-hatk)+t(3hati+2hatj+7hatk)` மற்றும் தளம் `vecr=(hati+hatj-hatk)=8`-க்கான வெட்டுப்புள்ளி.
06:02View Solutionதவறான விடையை தேர்ந்தெடுக்க: ஒரு கோடானது x மற்றும் y மிகை அச்சுடன் `alpha=45^@. beta=60^@`ஐ ஏற்படுத்தினால் z-அச்சுடன் `(gamma)` ஏற்படுத்தும் கோணம் என்பது
05:25View Solutionதவறான விடையை தேர்ந்தெடுக்க: `overlinePR=2hati+hatj+hatk, overlineQS=-hati+3hatj+2hatk` எனில், நாற்கரம் PQRS-ன் மதிப்பு
06:14View Solutionபொருத்துக: கோடுகள் `vecr=veca+svecb` மற்றும் `vecr=vecc+tvecd`
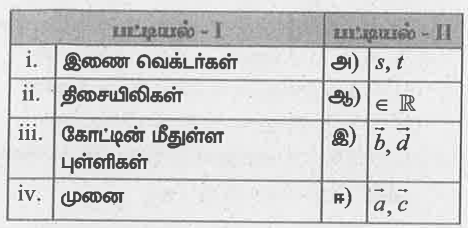 01:37View Solution
01:37View Solutionபொருத்துக: கொடுக்கப்பட்டுள்ள புள்ளி வழிச்செல்லும் இரண்டு இணையற்ற வெக்டர்களுக்கு இணையான தளத்தின் சமன்பாடு
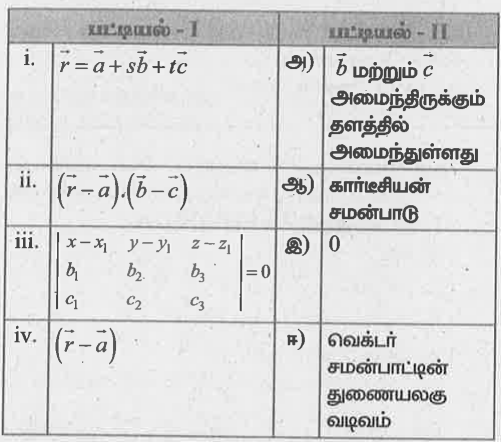 01:41View Solution
01:41View Solutionபொருத்துக: தளத்தின் வெட்டுத்துண்டு வடிவச் சமன்பாட்டுக்கு
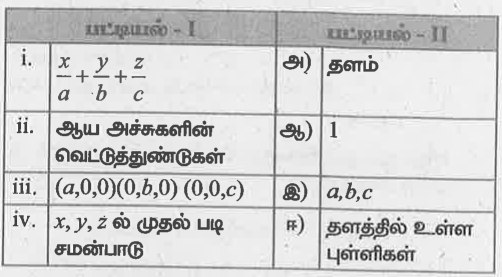 01:45View Solution
01:45View Solutionபொருத்துக: கோடுகளுக்கு `frac{x-1}{4}=frac{2-y}{6}=frac{z-4}{12}, frac{x-3}{-2}=frac{y-3}{3}=frac{5-z}{6}`
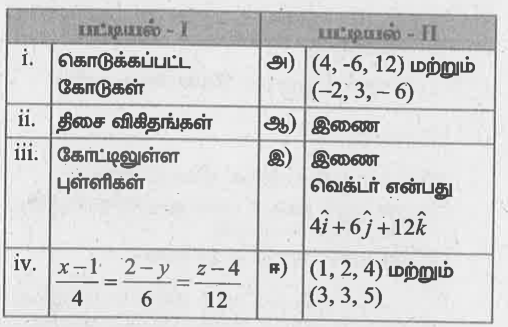 10:35View Solution
10:35View Solutionபொருத்துக: `[veca,vecb,vecc]` ஒரு தள வெக்டர்கள் எனில்
 04:18View Solution
04:18View Solution`veca=2hati+2hatj+3hatk,vecb=-hati+2hatj+hatk, vecc=3hati+hatj` பிறகு `veca+lamdavecb` ஆனது `vecc`-க்கு செங்குத்து எனில் lamda =
04:38View Solution`2hati-2hatj+hatk` என்ற வெக்டருக்கு இணையான 6 அலகுகள் அளவுடைய விசை ஒரு துணை (1, 2, 3)லிருந்து (5, 3, 7)-க்கு நகர்த்துகிறது. செய்யப்பட்ட வேலையைக் காண்க.
04:24View SolutionA(3, -1, 2) B(1, -1,-3) மற்றும் C(4, -3,1) ஆகிய உச்சிகளையும் முக்கோணத்தின் பரப்பைக் காண்க.
06:03View Solution`4hati-3hatj-2hatk` என்ற நிலை வெக்டரை உடைய P-யின் மீது செயல்படுகிற விசைகள் `2hati+7hatj`,`2hati-5hatj+6hatk`,`-hati+2hatj-hatk` ஆகும். `6hati+hatj-3hatk` வை நிலை வெக்டராக உடைய புள்ளி Q வை பொறுத்து விசைகளின் விளைவின் வெக்டர் திருப்பு திறன் காண்க.
05:03View SolutionA(2, -1, 3) மற்றும் B(4, 2,1) என்ற புள்ளிகள் வழிச் செல்லும் நேர்கோட்டின் கார்டீசியன் சமன்பாட்டைக் காண்க.
02:44View Solution(2, -1, 3) என்ற புள்ளி வழிச் செல்கிற மற்றும் `vecr=(hati+hatj)+t(2hati+hatj-2k)` என்ற கோட்டிற்கு இணையான கோட்டின் வெக்டர் சமன்பாடு துணையலகு வடிவத்தில் காண்க.
04:02View Solution(1, -1,2) வழிச் செல்கிற (2, 3, 3) ஐ திசை விகிதங்களாக கொண்ட செங்குத்தினை உடைய தளத்தின் வெக்டர் சமன்பாட்டின் துணையலகு வடிவம் காண்க.
02:43View Solutionதளங்கள் `vecr.(hati+2hatj+3hatk)=7` மற்றும் `vecr.(lambdahati+2hatj-7hatk)=26` செங்குத்து எனில் `lambda`-ன் மதிப்பைக் காண்க.
02:42View Solutionx+y+z-6=0 மற்றும் 2x+3y+4z+5=0 என்ற தளங்கள் வெட்டுக் கோடு வழிச் செல்லும் புள்ளி (1, 1, 1) ஐ கொண்டிருக்கும் தளத்தின் சமன்பாட்டைக் காண்க.
06:12View Solution`veca.vecb=veca.vecc=0` எனுமாறு அலகு வெக்டர்கள் `veca, vecb, vecc` என்க மற்றும் `vecb` மற்றும் `vecc`-க்கு இடையேயான கோணம் `pi/6`. நிரூபிக்க. `veca = pm2(bxxvecc)`.
04:35View Solution`3hati-5hatk, 2hati+7hatj`மற்றும் `hati+hatj+hatk` வெக்டர்களுமான ஒரு வெக்டாின் புள்ளி பெருக்கல்பலன் முறையே -1, 6 மற்றும் 5. வெக்டரைக் காண்க.
08:26View Solution(2, -1, 3) என்ற புள்ளி வழிச் செல்கிற மற்றும் `vecr=(hati+hatj)+t(2hati+hatj-2k)` என்ற கோட்டிற்கு இணையான கோட்டின் வெக்டர் சமன்பாடு துணையலகு வடிவத்தில் காண்க.
04:02View Solutionதளங்கள் 2x-3y+z-4=0 மற்றும் x-y+z+1=0-க்கான வெட்டுக்கோடு வழி செல்லும் மற்றும் தளம் x+2y-3z+6=0-க்கு செங்குத்தான தளத்தின் சமன்பாடு காண்க.
05:45View Solutionபின்வரும் ஜோடி கோடுகளுக்கு `frac{x-3}{3}=frac{y-8}{-1}=frac{z-3}{1}` மற்றும் `frac{x+3}{-3}=frac{y+7}{2}=frac{z-6}{4}` இடையேயான குறைந்தபட்ச தூரம் காண்க.
07:26View Solution`veca=hati-hatj,vecb=hatj-hatk,vecc=hatk-hati`எனில் `[veca-vecb,vecb-vecc,vecc-veca]` காண்க.
03:04View Solutionநிரூபிக்க. `[veca+vecb.vecb+vecc.vecc+veca]=2[vecavecbvecc]`
03:21View Solutionசெங்கோண முக்கோணத்தில் கர்ணத்தின் வர்க்கம் மற்ற இரு பக்கங்களின் வர்க்கங்களின் கூடுதலுக்கு சமம் என வெக்டர் முறையை பயன்படுத்தி நிரூபிக்க.
04:29View Solution`|veca|=5,|vecb|=6,|vecc|=7` மற்றும்`veca+vecb+vecc=vec0` எனில், `veca.vecb+vecb.vecc+vecc.veca` ஐக் காண்க.
02:50View Solution`2hati-hatj+k,3hati-4hatj-4hatk,hati-3hatj-5hatk` ஆகிய வெக்டர்கள் ஒரு செங்கோண முக்கோணத்தை அமைக்கும் எனக்காட்டுக.
05:06View Solution`frac{x-1}{3}=frac{y+1}{2}=frac{z-1}{5}` மற்றும் `frac{x-2}{4}=frac{y-1}{3}=frac{z+1}{-2}` வெட்டுவதில்லை எனக்காட்டுக.
05:58View Solution
EXAMPLE questions and complete solutions for chapter வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் of SURA MATHS (TAMIL) of Class 12
