Complete Solutions to EXERCISE of chapter தொகை நுண்கணிதத்தின் பயன்பாடுகள் of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | தொகை நுண்கணிதத்தின் பயன்பாடுகள் |
| SURA PUBLICATION(TAMIL) | EXERCISE |
| Number Of Questions | 92 |
| Academic Year | 2023-24 |
{1.1, 1.2, 1.3, 1.4, 1.5} எனும் பிரிவினையுடன் இடது-முனை விதியைப் பயன்படுத்தி `int_1^1.5 xdx`-க்கு தோராய மதிப்பு காண்க.
03:51View Solution{1.1, 1.2, 1.3, 1.4, 1.5} எனும் பிரிவினையுடன் வலது-முனை விதியைப் பயன்படுத்தி `int_1^1.5 x^2dx`-க்கு தோராய மதிப்பு காண்க.
03:23View Solution{1.1, 1.2, 1.3, 1.4, 1.5} எனும் பிரிவினையுடன் நடு-முனை விதியைப் பயன்படுத்தி `int_1^1.5 (2-x)dx`-க்கு தோராய மதிப்பு காண்க.
04:20View Solutionகீழ்க்காணும் தொகையீடுகளை கூட்டலின் எல்லைகளாக கணக்கிடுக: `int_0^1(5x+4)dx`
05:14View Solutionகீழ்க்காணும் தொகையீடுகளை கூட்டலின் எல்லைகளாக கணக்கிடுக: `int_1^2(4x^2-1)dx`
06:17View Solutionபின்வரும் வரையறுத்த தொகையிடலின் மதிப்பு காண்க : `int_3^4frac{dx}{x^2-4}`
02:30View Solutionபின்வரும் வரையறுத்த தொகையிடலின் மதிப்பு காண்க : `int_-1^1frac{dx}{x^2+2x+5}`
07:06View Solutionபின்வரும் வரையறுத்த தொகையிடலின் மதிப்பு காண்க : `int_0^1sqrtfrac{1-x}{1+x}dx`
06:38View Solutionபின்வரும் வரையறுத்த தொகையிடலின் மதிப்பு காண்க : `inte^x(frac{1+sinx}{1+cosx})dx`
06:10View Solutionபின்வரும் வரையறுத்த தொகையிடலின் மதிப்பு காண்க : `int_0^frac{pi}{2}sqrt(costheta)sin^3thetad theta`
03:44View Solutionபின்வரும் வரையறுத்த தொகையிடலின் மதிப்பு காண்க : `int_0^1frac{1-x^2}{(1+x^2)^2}dx`
04:08View Solutionபின்வரும் வரையறுத்த தொகையிடல்களை தொகையிடலின் பண்புகளைப் பயன்படுத்தி மதிப்பு காண்க : `int_-5^5xcos(frac{e^x-1}{e^x+1})dx`
03:12View Solutionபின்வரும் வரையறுத்த தொகையிடல்களை தொகையிடலின் பண்புகளைப் பயன்படுத்தி மதிப்பு காண்க : `int_-frac{pi}{2}^frac{pi}{2}(x^3+xcosx+tan^5x+1)dx`
05:30View Solutionபின்வரும் வரையறுத்த தொகையிடல்களை தொகையிடலின் பண்புகளைப் பயன்படுத்தி மதிப்பு காண்க : `int_-frac{pi}{4}^frac{pi}{4}sin^2xdx`
03:50View Solutionபின்வரும் வரையறுத்த தொகையிடல்களை தொகையிடலின் பண்புகளைப் பயன்படுத்தி மதிப்பு காண்க : `int_0^(2pi)xlog(frac{3+cosx}{3-cosx})dx`
04:26View Solutionபின்வரும் வரையறுத்த தொகையிடல்களை தொகையிடலின் பண்புகளைப் பயன்படுத்தி மதிப்பு காண்க : `int_0^(2pi)sin^4xcos^3xdx`
05:24View Solutionபின்வரும் வரையறுத்த தொகையிடல்களை தொகையிடலின் பண்புகளைப் பயன்படுத்தி மதிப்பு காண்க : `int_0^1|5x-3|dx`
04:39View Solutionபின்வரும் வரையறுத்த தொகையிடல்களை தொகையிடலின் பண்புகளைப் பயன்படுத்தி மதிப்பு காண்க : `int_0^(sin^2x)sin^-1sqrttdt+int_0^(cos^2x)cos^-1sqrttdt`
05:36View Solutionபின்வரும் வரையறுத்த தொகையிடல்களை தொகையிடலின் பண்புகளைப் பயன்படுத்தி மதிப்பு காண்க : `int_0^1frac{log(1+x)}{1+x^2}dx`
09:09View Solutionபின்வரும் வரையறுத்த தொகையிடல்களை தொகையிடலின் பண்புகளைப் பயன்படுத்தி மதிப்பு காண்க : `int_0^pifrac{xsinx}{1+sinx}dx`
07:31View Solutionபின்வரும் வரையறுத்த தொகையிடல்களை தொகையிடலின் பண்புகளைப் பயன்படுத்தி மதிப்பு காண்க : `int_frac{pi}{8}^frac{3pi}{8}frac{1}{1+sqrt(tanx)}dx`
06:43View Solutionபின்வரும் வரையறுத்த தொகையிடல்களை தொகையிடலின் பண்புகளைப் பயன்படுத்தி மதிப்பு காண்க : `int_0^pix[sin^2(sinx)+cos^2(cosx)]dx`
03:23View Solutionபின்வருவனவற்றை மதிப்பிடக : `int_0^1x^3e^(-2x)dx`
06:34View Solutionபின்வருவனவற்றை மதிப்பிடக : `int_0^1frac{sin(3tan^-1x)tan^-1x}{1+x^2}dx`
04:52View Solutionபின்வருவனவற்றை மதிப்பிடக : `int_0^frac{1}{sqrt2}frac{e^(sin^-1x)sin^-1x}{sqrt(1-x^2)}dx`
04:53View Solutionபின்வருவனவற்றை மதிப்பிடக : `int_0^frac{pi}{2}x^2cos2xdx`
07:09View Solutionபின்வருவனவற்றை திப்பிடக : `int_0^{pi} frac{dx}{1+5cos^2x}`
03:03View Solutionபின்வருவனவற்றை மதிப்பிடக : `int_0^frac{pi}2}frac{dx}{5+4sin^2x}`
06:45View Solutionபின்வருவனவற்றை மதிப்பிடக : `int_0^frac{pi}{2}sin^10xdx`
02:25View Solutionபின்வருவனவற்றை மதிப்பிடக : `int_0^frac{pi}{2}cos^7xdx`
01:18View Solutionபின்வருவனவற்றை மதிப்பிடக : `int_0^frac{pi}{4}sin^(6)2xdx`
02:53View Solutionபின்வருவனவற்றை மதிப்பிடக : `int_0^frac{pi}{6}sin^(5)3xdx`
02:37View Solutionபின்வருவனவற்றை மதிப்பிடக : `int_0^frac{pi}{2}sin^2xcos^4xdx`
02:24View Solutionபின்வருவனவற்றை மதிப்பிடக : `int_0^(2pi)sin^7frac{x}{4}dx`
02:42View Solutionபின்வருவனவற்றை மதிப்பிடக : `int_0^frac{pi}{2}sin^3thetacos^5thetad theta`
03:03View Solutionபின்வருவனவற்றை மதிப்பிடக : `int_0^1x^2(1-x)^3dx`
01:29View Solutionபின்வருவனவற்றை மதிப்பிடக : `int_0^oox^5e^(-3x)dx`
01:13View Solutionபின்வருவனவற்றை மதிப்பிடக : `int_0^frac{pi}{2}frac{e^(-tanx)}{cos^6x}dx`
04:40View Solution`int_0^ooe^(-ax^2)x^3dx=32,alpha>0` எனில் `alpha`-ன் மதிப்பைக் காண்க.
04:39View Solution2x-y+1=0, y=-1, y=3 மற்றும் x- அச்சு ஆகியவற்றால் அடைபடும் அரங்கத்தின் பரப்பைக் காண்க.
06:20View Solution2x-y+1=0, y=-1, y=3 மற்றும் x- அச்சு ஆகியவற்றால் அடைபடும் அரங்கத்தின் பரப்பைக் காண்க.
06:20View Solutionவளைவரை `2+x-x^2+y=0`, x-அச்சு, x=-3 மற்றும் x=3 ஆகியவற்றால் அடைபடும் அரங்கத்தின் பரப்பைக் காண்க.
11:43View Solutiony=tanx, y=cotx மற்றும் கோடுகள் x=0, `x=frac{pi]{2}`, y=0 ஆகியவற்றால் அடைபடும் அரங்கத்தின் பரப்பைக் காண்க.
05:18View Solutionபரவளையம் `y^2=x` மற்றும் கோடு y=x-2 ஆகியவற்றால் அடைபடும் அரங்கத்தின் பரப்பைக் காண்க.
06:21View Solutionஒரு குடும்பத் தலைவர், x=0, x=4, y=4 மற்றும் y=0 ஆகியவற்றால் அடைபடும் சதுரநிலத்தின் பரப்பை `y^2=4x` மற்றும் `x^2=4y` என்ற வளைவரைகளின் வாயிலாக தன்னுடைய மனைவி, மகள் மற்றும் மகன் ஆகியோர்களுக்கு மூன்று சமபாகங்களாகப் பிரிய விரும்புகிறார். அவ்வாறு பிரிக்க இயலுமா? பிரிக்க இயலும் எனில் ஒவ்வொருவருக்கும் கிடைக்கும் பரப்பைக் காண்க.
08:15View Solution`x^2+y^2=16` என்ற வட்டத்திற்கும் `y^2=6x` என்ற பரவளையத்திற்கும் பொதுவான அரங்கத்தின் பரப்பைக் காண்க.
10:42View Solution`y=2x^2, y=0` மற்றும் x=1 ஆகியவற்றால் அடைபடும் அரங்கத்தின் பரப்பை x-அச்சைப் பொருத்துச் சுழற்றுவதால் உருவாகும் திடப்ப பொருளின் கன அளவைக் காண்க.
02:50View Solution`y=e^(-2x), y=0, x=0` மற்றும் x=1 ஆகியவற்றால் அடைபடும் அரங்கத்தின் பரப்பை x-அச்சைப் பொருத்துச் சுழற்றுவதால் உருவாகும் திடப்ப பொருளின் கன அளவைக் காண்க.
02:32View Solution`x^2=1+y` மற்றும் y=3 ஆகியவற்றால் அடைபடும் பரப்பை x அச்சைப் பொருத்துச் சுழற்றுவதால் உருவாகும் திடப் பொருளின் கன அளவைக் காண்க.
02:58View Solutionஒரு கொள்கலன் (container) ஆனது நேர்வட்டக் கூம்பின் இடைக்கண்டம் (frustum of a cone) வடிவில் படத்தில் உள்ளவாறு அமைத்துள்ளது. எனில் அதன் கன அளவைத் தொகுதியிடலைப் பயன்படுத்தி காண்க.
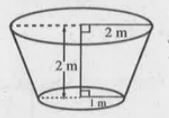 04:38View Solution
04:38View Solutionஒரு தர்பூசணியானது நீள்வட்ட திண்ம வடிவில் (ellipsoid shape) உள்ளது. இந்த நீள்வட்ட தின்மத்தை பெற நெட்டச்சின் நீளம் 20 செ.மீ . குற்றச்சின் நீளம் 10 செ.மீ கொண்ட நீள்வட்டத்தை நெட்டச்சைப் பொருத்து சுழற்ற வேண்டும் எனில் தர்பூசணியின் கன அளவை தொகுதியிடலைப் பயன்படுத்தி காண்க.
05:42View Solution`int_0^frac{2}{3}frac{dx}{sqrt(4-9x^2)}` இன் மதிப்பு
03:19View Solution`int_-1^2|x|dx` இன் மதிப்பு
02:23View Solutionஒவ்வொரு `ZZ`-க்கும் `int_0^pie^(cos^2x)cos^3[(2n+1)x]dx` இன் மதிப்பு
04:04View Solution`int_-frac{pi}{2}^frac{pi}{2}sin^2xcosxdx` இன் மதிப்பு
02:54View Solution`int_-4^4[tan^-1(frac{x^2}{x^4+1})+tan^-1(frac{x^4+1}{x^2})]dx` இன் மதிப்பு
03:47View Solution`int_-frac{pi}{4}^frac{pi}{4}(frac{2x^7-3x^5+7x^3-x+1}{cos^2x))dx` இன் மதிப்பு
05:13View Solution`f(x)=int_0^xtcostdt`, எனில் `frac{df}{dx}`
02:44View Solution`y^2=4x` என்ற பரவளையத்திற்கும் அதன் செவ்வகலத்திற்கும் இடையே பரப்பானது
02:03View Solution`int_0^1x(1-x)^99dx` இன் மதிப்பு
02:56View Solution`int_0^pifrac{dx}{1+5^cosx}` இன் மதிப்பு
03:41View Solution`frac{Gamma(n+2)}{Gamma(n)}=90` எனில் n இன் மதிப்பு
02:22View Solution`int_0^frac{pi}{6}cos^(3)3xdx` இன் மதிப்பு
02:34View Solution`int_0^pisin^4xdx` இன் மதிப்பு
02:52View Solution`int_0^ooe^(-3x)x^2dx` இன் மதிப்பு
01:42View Solution`int_a^afrac{1}{4+x^2}dx=frac{pi}{8}` எனில் a இன் மதிப்பு
02:25View Solution`y^2=x(a-x)` என்ற வளைவரையில் அடைபடும் அரங்கத்தின் பரப்பை X - அச்சைப் பொருத்து சுழற்றுவதால் உருவாகும் திடப்பொருளின் கன அளவு
02:48View Solution`f(x)=int_1^xfrac{e^sinu}{u}du,x>1` மற்றும் `int_1^3frac{e^(sinx^2)}{x}dx=frac{1}{2}[f(a)-f(1)],` எனில் a
03:29View Solution`int_0^1(sin^-1x)^2dx` இன் மதிப்பு
07:17View Solution`int_0^a(sqrt(a^2-x^2))^2dx` இன் மதிப்பு
03:32View Solution`int_0^xf(t)dt=x+int_x^1tf(t)dt,`எனில் f(1) இன் மதிப்பு
02:41View Solution`int_0^frac{pi}{2}frac{dx}{1+tanx}`-இன் மதிப்பு
05:44View Solution`int_-frac{pi}{2}^frac{pi}{2}sqrtfrac{1-cos2x}{2}dx` -இன் மதிப்பு
03:32View Solution`int_1^sqrt3frac{dx}{1+x^2}=`
02:08View Solution`int_0^(2a)f(x)dx=2int_0^af(x)` எனில்
01:50View Solution`int_-pi^pisin^3xcos^3xdx`-இன் மதிப்பு
02:36View Solution`int_-1^1xdx=` ................................
01:37View Solution`int_0^(2a)f(x)dx=2int_0^af(x)` எனில்
01:50View Solution`frac{x^2}{4}+frac{y^2}{9}=1` என்ற நீள்வட்டத்தின் பரப்பு ................
05:34View Solutionதவறான விடையை தேர்ந்தெடுக்க : `int_0^frac{pi}{2}frac{cos^frac{5}{3}x}{cos^frac{5}{3}x+sin^frac{5]{3}x}dx=`
View Solutionதவறான விடையை தேர்ந்தெடுக்க : `int_a^bf(x)dx=`
View Solutionபொருத்துக : சரியான பொருத்தமானது.
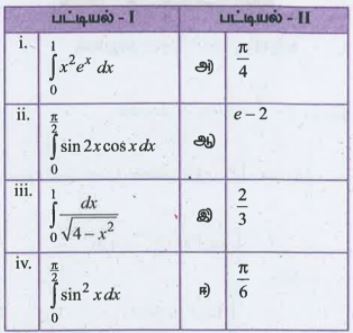 View Solution
View Solutionபொருத்துக : சரியான பொருத்தமானது.
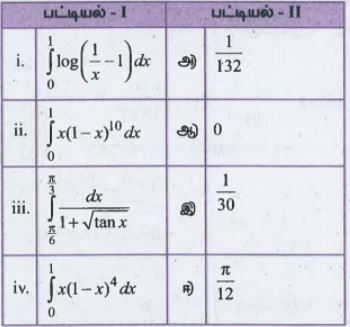 View Solution
View Solution`int_0^frac{pi}{2}log(tanx)dx=0` என நிரூபிக்க
02:41View Solutionமதிப்பிடுக : `int_0^1frac{e^x}{1+e^(2x)}dx`
02:11View Solutionமதிப்பிடுக :`int_1^2frac{3x}{9x^2-1}dx`
02:53View Solutionமதிப்பிடுக : `int_0^frac{pi}{2}frac{sqrt(cotx)}{sqrt(cotx)+sqrt(tanx)}dx`
03:37View Solutionமதிப்பிடுக : `int_-1^1log(frac{2-x}{2+x})dx`
02:39View Solutionமதிப்பிடுக : `int_0^frac{pi}{2}frac{sinx}{1+cos^2x}dx`
03:47View Solution`int_0^frac{pi}{2}sin2xlog(tanx)dx=0` என நிரூபிக்க.
03:30View Solutiony=2x+1, y=3x+1 மற்றும் x=4 ஆகியவற்றை பக்கங்களாக கொண்ட முக்கோணத்தின் பரப்பை தொகை நுண் கணிதத்தை பயன்படுத்தி காண்க.
05:10View Solution`x=t^2` மற்றும் `y=t-frac{t^3}{3}` ஆகியவற்றால் அடைபடும் அரங்கத்தின் பரப்பை x-அச்சைப் பொருத்துச் சுழற்றுவதால் உருவாகும் திடப்ப பொருளின் கன அளவை காண்க.
06:11View Solution
EXERCISE questions and complete solutions for chapter தொகை நுண்கணிதத்தின் பயன்பாடுகள் of SURA MATHS (TAMIL) of Class 12
