Complete Solutions to EXERCISE of chapter நிகழ்தகவு பரவல்கள் of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | நிகழ்தகவு பரவல்கள் |
| SURA PUBLICATION(TAMIL) | EXERCISE |
| Number Of Questions | 45 |
| Academic Year | 2023-24 |
X என்பது மூன்று சீரான நாணயங்களை ஒரே சமயத்தில் ஒரு முறைச் சீண்டும்போது விழும் பூக்களின் எண்ணிக்கை என்க. சமவாய்ப்பு மாறியான X-இன் மதிப்புகளையும் அதன் நேர்மாறு பிம்பங்களில் உள்ள புள்ளிகளின் எண்ணிக்கையையும் காண்க.
03:58View Solution52 சீட்டுகட்டுகளை உடைய ஒரு சீட்டுக்கட்டிலிருந்து இரு சீட்டுகள் ஒரே சமயத்தில் சமவாய்ப்பு முறையில் எடுக்கப்படுகின்றன. அவ்வாறு எடுக்கப்பட்ட சீட்டுகள் கருப்பாக இருப்பின் சமவாய்ப்பு மாறியான X-இன் மதிப்புகளையும் அதன் நேர்மாறு பிம்பங்களில் உள்ள புள்ளிகளின் எண்ணிக்கையையும் காண்க.
05:21View Solutionமகன் மற்றும் மகளுக்கு சமவாய்ப்பு நிகழ்தகவுகள் எனக் கருதி 4 குழந்தைகள் கொண்ட ஒரு குடும்பத்தில் உள்ள மகள்களின் எண்ணிக்கைக்கு நிகழ்தகவு நிறை சார்பினையும் குவிவு பரவல் சார்பினையும் காண்க.
12:03View Solutionஒரு பால் விற்பனையகத்தில் விநியோகிக்கப்படும் பாலின் அளவு சமவாய்ப்பு மாறி X என்க. குறைந்தபட்சம் 200 லிட்டர்கள் மற்றும் அதிகபட்சம் 600 லிட்டர்களுடன் நிகழ்தகவு அடர்த்தி சார்பு இன் பிற மதிப்புகளுக்கு `f(x)={(k, 200lexle600),(0, x இன் பிற மதிப்புகளுக்கு ):}` (i) k மதிப்பு காண்க. (ii) பரவல் சார்பு காண்க. (iii) 300 லிட்டர்கள் மற்றும் 500 லிட்டர்களுக்கிடையே தினசரி விற்பனை இருப்பதற்கான நிகழ்தகவு காண்க.
11:18View Solutionசமவாய்ப்பு மாறி X-யின் நிகழ்தகவு அடர்த்தி சார்பு `f(x)={(ke^((-x)/3),,x>0),(0,,xle0):}` எனில் (i) k மதிப்பு காண்க. (ii) பரவல் சார்பு காண்க. (iii) `P(X<3)` (iv) `P(xle5)` (v) `P(X<4)`
09:35View Solutionநான்கு சிவப்பு பந்துகள் மற்றும் மூன்று கருப்பு பந்துகள் கொண்ட ஒரு கூடையிலிருந்து பதிலீடாக இடாது அடுத்தடுத்து இரு பந்துகள் வெளியில் எடுக்கப்படுகின்றன. சிவப்பு பந்து வெளியில் எடுக்கும் சாத்திய கூறுகளை X என்க. X -ன் நிகழ்தகவு நிறை சார்பையும் சராசரியையும் காண்க.
10:41View Solution`mu` மற்றும் `sigma^2` ஆகியவை முறையே தனிநிலை சமவாய்ப்பு மாறி X-ன் சராசரி மற்றும் பரவற்படி மற்றும் E(X + 3)=10 மற்றும்` E(X + 3)^2=116`, எனில் µ மற்றும் `σ^2`காணக
04:21View Solutionநான்கு சீரான நாணயங்கள் ஒரு முறை சுண்டப்படுகின்றன. தலைகளின் எண்ணிக்கை நிகழ்விற்கு நிகழ்தகவு நிறை சார்பு, சராசரி, மற்றும் பரவற்படி காண்க.
11:52View Solutionஒரு பயணிகள் இரயில் ஒவ்வொரு அரை மணி நேரத்திற்கும் ஒரு நிலையத்திற்கு சரியான நேரத்தில் வந்து சேரும். ஒவ்வொரு நாள் காலை யிலும், ஒரு மாணவர் தனது வீட்டிலிருந்து இரயில் நிலையத்திற்கு செல்கிறார். மாணவர் ரயில் நிலையத்தை அடையும் நேரத்திலிருந்து ரயிலுக்காக காத்திருக்கும் நேரத்தை X என நிமிடங்களில் குறிக்கலாம். X – ன் நிகழ்தகவு `f(x)={(1/30 ,0 < x < 30),(0, பிற மதிப்புகளுக்கு):}` எனில் சமவாய்ப்பு மாறி X-ன் நிகழ்தகவு அடர்த்தி சார்பு
03:10View Solutionகணினி தயாரிக்கப்படும் போது ஆயிரக்கணக்கான மணிநேரம் பயன்படுத்தப்படும் ஒருமின்னணு சாதனமொன்றின் பழுதடையும் நேரத்தின் அடர்த்தி சார்பு `f(x)={(3e^(-3x), x>0),(0,பிற மதிப்புகளுக்கு):}` ஆகும். இம்மின்னனு சாதனத்தின் எதிர்பாக்கப்படும் ஆயிட்காலத்தை காண்க.
04:42View Solutionசமவாய்ப்பு மாறி X-ன் சராசரி நிகழ்தகவு அடர்த்தி சார்பு `f(x)={(16xe^(-4x), x>0),(0,xle0):}` ஆகும் சமவாய்ப்பு மாறி X-ன் நிகழ்தகவு அடர்த்தி சார்பு
06:24View Solution600 டிக்கெட்டுகள் கொண்ட ஒரு லாட்டரியில் ஒரு பரிசு ₹.200 -க்கும் நான்கு பரிசுகள் ₹.100 -க்கும் , ஆறு பரிசுகள் ₹.50 -க்கும் எனக்கொடுக்கிறது. டிக்கெட் செலவு ₹.2 என்றால், ஒரு டிக்கெட்டின் எதிர்பார்க்கப்படும் வெற்றி தொகையைக் கண்டறியவும்.
03:52View Solutionகீழ்காணும் ஈருறுப்பு பரவல் B(n, p)-க்காக P(X = k) என்பதைக் கணிக்க.(i) `n=6,p=1/3,k=3` (ii) `n=10,p=1/5,k=4` (iii) `n=9,p=1/2,k=7`
07:38View Solutionஎந்த முயற்சியிலும் ஒரு இலக்கை திரு.Q தாக்க நிகழ்தகவு `1/4` ஆகும். பத்து முறை இலக்கை அவர் தாக்க முயற்சிக்கிறார் எனக் கொள்க. இலக்கைத் தாக்க (i) சரியாக 4 முறைகள் (ii) குறைந்தபட்சம் ஒரு முறை தாக்குவதற்கு ஆகியவற்றிக்கான நிகழ்தகவு காண்க.
06:39View Solutionகீழ்காணும் சோதனைகளில் ஈருறுப்பு பரவலைப் பயன்படுத்தி சமவாய்ப்பு மாறி X-ன் சராசரி மற்றும் பரவற்படி காண்க. (i) 100 தடவை ஒரு சீரான நாணயம் சுண்டப்படுகிறது. தலைகளின் எண்ணிக்கையை X குறிக்கிறது. (ii) 240 தடவை ஒரு சீரான பகடை சுண்டப்படுகிறது. எண் நான்கு தோன்றுவதற்கான எண்ணிக்கையை X குறிக்கிறது.
05:46View Solutionஒரு மின்சோதனையில் ஒரு குறிப்பிட்ட சாதனத்தின் தாங்கும் திறனுக்கான நிகழ்தகவு `3/4`. சோதிக்கப்பட்ட ஐந்தில் சரியாக மூன்று சாதனங்களின் தாங்கு திறனுக்கான நிகழ்தகவைக் கண்டறிக.
05:44View Solutionஒரு உற்பத்தியாளரிடமிருந்து ஒரு குறிப்பிட்ட மின்வகைக் கருவியை ஒரு விற்பனையாளர் கொள்முதல் செய்கிறார். உற்பத்தியாளர் கருவியின் சதவீதம் 5 எனக் கூறுகிறார். கொள்முதல் செய்யப்பட்ட சரக்கிலிருந்து 10 பொருட்களை விற்பனையாளரின் பரிசோதகர் சமவாய்ப்பு முறையில் பரிசோதிக்கிறார். அவற்றுள் (i) குறைந்தபட்சம் ஒரு பழுதான பொருள் (ii) சரியாக இரு பொருட்கள் பழுதாக இருக்க நிகழ்தகவு காண்க.
07:43View Solutionஒரு பாதரச ஆவி விளக்கின் பயன்படும் காலம் குறைந்தபட்சம் 600 மணித்துளிகளுக்கான நிகழ்தகவு 0.9. எனில் அத்தகைய 12 விளக்குகளில் (i) சரியாக 10 விளக்குகளின் பயன்படும் காலம் குறைந்தபட்சம் 600 மணித்துளிகளுக்கான நிகழ்தகவு (ii) குறைந்தபட்சம் 11 விளக்குகளின் பயன்படும் காலம் குறைந்தபட்சம் 600 மணித்துளிகளுக்கான நிகழ்தகவு (iii) குறைந்தபட்சம் 2 விளக்குகளின் பயன்படும் காலம் குறைந்தபட்சம் 600 மணித்துளிகள் கூட இல்லாததற்கான நிகழ்தகவு ஆகியவற்றைக் காண்க.
08:26View Solutionஒரு ஈருறுப்பு சமவாய்ப்பு மாறி X -ன் சராசரி மற்றும் திட்ட விலக்கம் முறையே 6 மற்றும் 2 ஆகும். (i) நிகழ்தகவு நிறை சார்பு (ii) P(X=3) (iii) `P(Xge2)` ஆகியவற்றைக் காண்க.
07:52View Solution4P(X = 4) = P(X = 2) மற்றும் n = 6 எனும்படி உள்ள X~B(n,p)-ன் பரவலின், சராசரி மற்றும் திட்டவிலக்கம் ஆகியவற்றைக் காண்க.
04:58View Solutionஒரு விளையாட்டில் அறுபக்க பகடையை விளையாடுபவர் உருட்டுகிறார். பகடை எண் 6-ஐக் காட்டினால், விளையாடுபவர் ₹36 வெல்லுவார், இல்லையெனில் `₹k^2`, தோற்பார். இங்கு k என்பது பகடை காட்டும் எண். k={1,2,3,4,5} விளையாட்டில் எதிர்பாக்கப்படும் வெல்லும் தொகை ₹.
04:33View Solution1,2,3,4,5,6 எண்ணிடப்பட்ட அறுபக்க பகடையும் 1,2,3,4 என எண்ணிடப்பட்ட நான்கு பக்க பகடையும் சோடியாக உருட்டப்பட்டு இரண்டும் காட்டும் எண்களின் கூட்டல்தொகை தீர்மானிக்கப்படுகிறது. இந்த கூட்டலைத் குறிக்கும் சமவாய்ப்பு மாறி X என்க. இனி 7 - இன் நேர்மாறு பிம்பத்தின் உறுப்புகளின் எண்ணிக்கை
03:26View Solutionn = 25 மற்றும் p = 0.8 என்று உள்ள ஈருறுப்பு பரவல் கொண்ட சமவாய்ப்பு மாறி X எனில் X-ன் திட்ட விலக்கத்தின் மதிப்பு
01:40View Solutionn முறை சுண்டப்படும் ஒரு நாணயத்தினால் பெறப்படும் தலை மற்றும் பூக்களின் எண்ணிக்கை வேறுபாட்டை X குறிக்கிறது என்க. X -இன் சாத்திய மதிப்புகள்
03:42View Solution`f(x)=1/12,a < x < b` எனும் சார்பு ஒரு தொடர்ச்சியான சமவாய்ப்பு மாறியின் நிகழ்தகவு அடர்த்தி சார்பினைக் குறிக்கிறது எனில், பின்வருவனவற்றுள் எது 1 மற்றும் –இன் மதிப்புகளாக இராது?
03:00View Solutionஒரு கால்பந்தாட்ட அரங்கிற்கு ஒரே பள்ளியிலிருந்து நான்கு பேருந்துகள் 160 மாணவர்களை ஏற்றிக்கொண்டு வருகிறது. அப்பேருந்துகளில் முறையே 42,36,34 மற்றும் 48 மாணவர்கள் பயணிக்கின்றனர். சமவாய்ப்பு முறையில் ஒரு மாணவர் தேர்ந்தெடுக்கப்படுகிறார். அவ்வாறு சமவாய்ப்பு முறையில் தேர்ந்தெடுக்கப்பட்ட மாணவர் பயணிக்கும் பேருந்திலுள்ள மாணவர்களின் எண்ணிக்கையை X குறிக்கிறது என்க. நான்கு பேருந்து ஓட்டுனர்களில் ஒருவர் சமவாய்ப்பு முறையில் தேர்ந்தெடுக்கப்படுகின்றனர். அவ்வாறு தேர்ந்தெடுக்கப்பட்ட ஓட்டுநர் ஓட்டி வரும் பேருந்திலுள்ள மாணவர்களின் எண்ணிக்கையை Y குறிக்கிறது என்க. இனி E(X) மற்றும் E(Y)முறையே
03:45View Solutionஇரு நாணயங்கள் சுண்டப்படுகின்றன. முதல் நாணயத்தில் தலை கிடைப்பதற்கான நிகழ்தகவு 0.6 மற்றும் இரண்டாவது நாணயத்தின் மூலம் தலை கிடைக்க நிகழ்தகவு 0.5 ஆகும். சுண்டி விடுதலின் முடிவுகள் சார்பற்றவை எனக் கருதுக. X என்பது மொத்த தலைகளின் எண்ணிக்கையைக் குறிக்கிறது என்க. E(X)-ன் மதிப்பு
01:02View Solutionபலவுள் தேர்வு ஒன்றில் 5 வினாக்கள் ஒவ்வொன்றிற்கும் 3 சாத்தியமானக் கவனச் சிதறல் விடைகள் உள்ளது. ஊகத்தின் அடிப்படையில் 4 அல்லது அதற்கு மேல் சரியான விடையை ஒரு மாணவர் அளிப்பதற்கான நிகழ்தகவு
03:55View SolutionP{X=0}=1-P{X=1} மற்றும் E[X] = 3 Var(X), எனில், P{X=0} காண்க.
04:45View Solutionஎதிர்பார்ப்பு மதிப்பு 6 மற்றும் பரவற்படி 2.4 கொண்ட ஒரு ஈருறுப்பு சமவாய்ப்பு மாறி X எனில் P(X=5)-இன் மதிப்பு
04:07View Solution0, மற்றும் 2 ஆகிய மதிப்புகளில் ஒன்றை X கொள்கிறது என்க. ஏதோ ஒரு மாறிலி k-விற்கு P(X = i-1), i = 1, 2 மற்றும் `P(X=0)=1/7` எனில் k -இன் மதிப்பு காண்க.
02:48View Solutionபின்வருவனவற்றுள் எது தனிநிலை சமவாய்ப்பு மாறி? I.ஒரு நாளில் ஒரு குறிப்பிட்ட சமிக்கையைக் கடக்கும் மகிழுந்துகளின் எண்ணிக்கை II. ஒரு குறிப்பிட்ட கணத்தில் தொடர்வண்டி பயணச் சீட்டு வாங்க வரிசையில் காத்திருக்கும் பயணிகளின் எண்ணிக்கை. III. ஒரு தொலைபேசி அழைப்பை நிறைவு செய்யும் காலம்.
02:15View Solutionஒரு சம வாய்ப்பு மாறியின் நிகழ்தகவு அடர்த்தி சார்பு
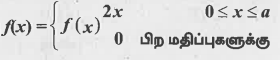 01:07View Solution
01:07View Solutionஒரு நிகழ்தகவு மாறியின் நிகழ்தகவு சார்பு கீழ்க்காணுமாறு வரையறுக்கப்படுகிறது:
 எனில், E(X) - க்கு சமமான மதிப்பு01:45View Solution
எனில், E(X) - க்கு சமமான மதிப்பு01:45View Solutionசராசரி 0.4 கொண்ட ஒரு பெர்னோலி பரவல் X எனில் (2X-3)-ன் பரவல்
02:13View Solutionஈருறுப்பு மாறி X ஆறு முயற்சிகளில் 9P(X=4) = P(X=2) எனும் தெடர்பினை அனுசரிக்கிறது எனில் வெற்றியின் நிகழ்தகவு
03:28View Solutionஒரு கணினி விற்பனையாளர் தனது கடந்த கால அனுபவத்திலிருந்து தனது காட்சி கூடத்திற்குள் நுழையும் ஒவ்வொரு இருபது வாடிக்கையாளர்களில், ஒருவருக்கு கணினியை விற்கிறார் என்பது தெரியும்.அடுத்த மூன்று வாடிக்கையாளர்களில் சரியாக இரண்டு பேருக்கு அவர் ஒரு கணினியை விற்கும் நிகழ்தகவு என்ன?
02:57View Solution`F(x)=1/2,E(x^2)=1/4` எனில் var(x) =
01:12View Solutionx இன் நிகழ்தகவு அடர்த்திச் சார்பு `f(x)=cx^2,0 < x < 2` எனில் c =
01:33View Solution`Var(2x+5)=` _______.
01:49View Solutionஈருறுப்பு பரவலின் பரவற்படி _______`
01:13View Solutionஒரு ஈருறுப்பு பரவலின் சராசரி மற்றும் திட்ட விலக்கம் முறையே 12 மற்றும் 2 எனில்
01:31View Solutionஒரு சமவாய்ப்பு மாறி X இன் நிகழ்தகவு நிறைச் சார்பு
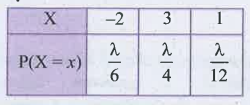 எனில்01:38View Solution
எனில்01:38View Solutionஒரு பெர்னோலி பரவலுக்கு
01:28View Solutionபொருத்துக:
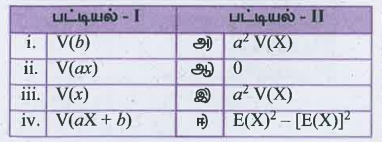 02:21View Solution
02:21View Solution
EXERCISE questions and complete solutions for chapter நிகழ்தகவு பரவல்கள் of SURA MATHS (TAMIL) of Class 12
