சமவாய்ப்பு மாறி X-யின் நிகழ்தகவு அடர்த்தி சார்பு எனில் (i) k மதிப்பு காண்க. (ii) பரவல் சார்பு காண்க. (iii) (iv) (v)
Step by step video & image solution for சமவாய்ப்பு மாறி X-யின் நிகழ்தகவு அடர்த்தி சார்பு f(x)={(ke^((-x)/3),,x>0),(0,,xle0):} எனில் (i) k மதிப்பு காண்க. (ii) பரவல் சார்பு காண்க. (iii) P(X<3) (iv) P(xle5) (v) P(X<4) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
{1.1, 1.2, 1.3, 1.4, 1.5} எனும் பிரிவினையுடன் இடது-முனை விதியைப் பயன்படுத்தி ∫1.51xdx-க்கு தோராய மதிப்பு காண்க.
View Solutionsin−1(cosx),0≤x≤π-ன் மதிப்பு
View SolutionFind the zero of the polynomial :
(i)p(x)=x−3 (ii)q(x)=3x−4 (iii)p(x)=4x−7 (iv)q(x)=px+q,p≠0
(v)p(x)=4x (vi)p(x)=32x−1
View Solutionएक यादृच्छिक चर X का प्रायिकता बंटन निचे दिया गया है |
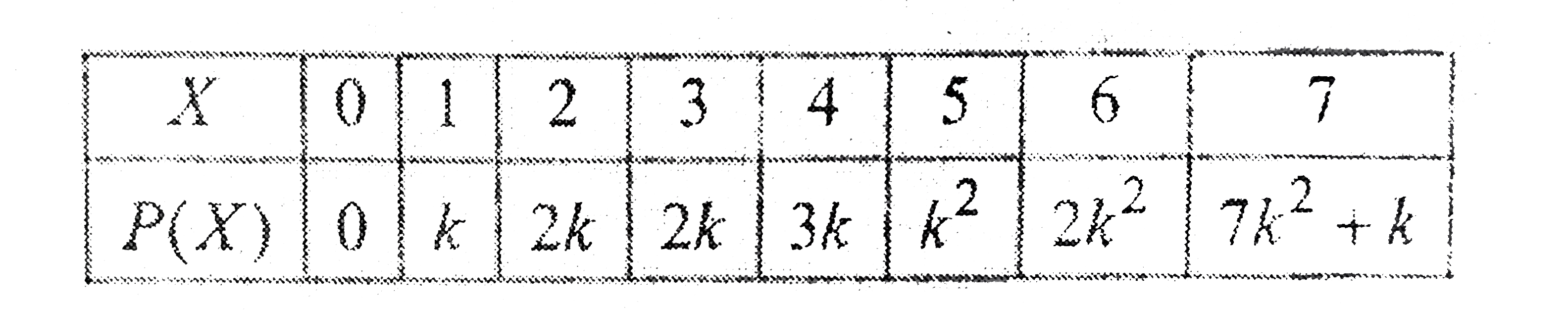
(i) K
(ii) P(X<3)
(iii) P(X>6)
(iv) P(0<X<3)
View Solutionनिम्नलिखित बहुपद के शून्यक ज्ञात कीजिए :
(i)p(x)=x−3(ii)q(x)=3x−4(iii)p(x)=4x−7(iv)q(x)=px+q,p≠0(v)p(x)=4x(vi)p(x)=33x−1
View SolutionThe probability density function of X is given by f(x) = {ke−x3for x>00for x≤0
Find (i) the value of k (ii) the distribution function (iii) P(X<3) (iv) P(5≤X) (v) P(X≤4) .
View SolutionA random variable X has the following probability distribution :

Determine
(i) k (ii) P(X<3)
(iii) P(X>6) (iv) P(0<X<3).
View Solutiona+1a=6எனில்,a^3 + 1/a^3 இன் மதிப்பு காண்க.
View SolutionFind the value of p (0), p (-1) and p (3) for each of the polynomials given below. (i) p(x)=x^(2)-3x (ii) p(x)=x^(3)+1 (iii) p(x)=(x-1)(x-2) (iv) p(x)=3x^(2)-2x+3
View SolutionA random variable X has the following probability distribution:

Determine (i) K (ii) P(X<3) (iii) P(X>6) (iv) P(0<X<3)
View SolutionA random variable X has the following probability distribution:

Determine (i)k,(ii)P(X<3),(iii)P(0<X<3),(iv)P(X>4).
View SolutionFind the zero of the polynomial :
(i)p(x)=x−3 (ii)q(x)=3x−4 (iii)p(x)=4x−7 (iv)q(x)=px+q,p≠0
(v)p(x)=4x (vi)p(x)=32x−1
View SolutionFind p(0), p(1) and p(-1) in the following polynomials.
i) p(x)= 3x+6
ii)p(x)= 3x2 + 6 x + 1
View SolutionA random variable X has the following probability distribution:
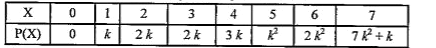
Determine
(i) k (ii) P (X < 3) (iii) P(X>6) (iv) P(0<X<3)
View SolutionThe probability distribution of X is as follows. Find (i) k, (ii) P[X lt 2] , (iii) P[X ge 3] , (iv) P[1 le X lt 4] , (v) F(2).
View Solution
