Complete Solutions to MATHEMATICS of chapter TS EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER (2018) of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | TS EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER (2018) |
| TS EAMCET | MATHEMATICS |
| Number Of Questions | 80 |
| Academic Year | 2023-24 |
Let X `={ ({:(a , b),(c,d):}) : a, b,c, d in R}` Define `f: X to R ` by f(A) = det (A) , `AA A in x `. then , f is
View SolutionLet `x ne 0 , |x| lt 1/2 ` and `f(x) = 1 + 2x + 4 x^2 + 8x^3 + ……` then , `f^(-1) (x) = `
03:27View SolutionFor all positive integers k, if the greatest divisor of `25^k + 12k -1` is d , then ` 4sqrtd` =
03:28View SolutionIf A =
 , then (AA')' =05:08View Solution
, then (AA')' =05:08View SolutionIf
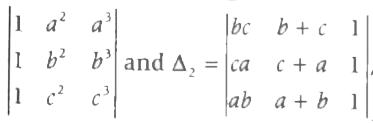 then `(Delta_1)/(Delta_2) = ` View Solution
then `(Delta_1)/(Delta_2) = ` View SolutionIf x = a , y = b, z = c is the solution of the system of simultaneous linear equations x + y + z = 4, x- y + z =2, x + 2y + 2z =1, then ab + bc + ca =
09:53View SolutionThe common roots of the equations
`z^3 + 2z^2 + 2z + 1 = 0 " and " z^(2018) + z^(2017) + 1 = 0`
satisfy the equationView SolutionThe area (in sq units) of the triangle whose vertices are the points represented by the complex numbers 0, z , `ze^(i alpha) ( 0 lt alpha lt pi)` is
07:14View SolutionIf `z + 1/z = 1 , ` then ` ( (z^(20) + 1) (z^(40) + 1) (z^(60) +1 ) )/(z^(60) )` =
View SolutionIf `omega_0 , omega_1 , ………, omega_( n - 1)` are the nth roots of unity then `(1 + 2 omega_0) ( 1 + 2 omega_1) (1 + 2 omega_2)…..(1 + 2omega_(n - 1) ) = `
04:17View SolutionIf `k in R` , then roots of `(x - 2) (x - 3) = k^2` are always `
02:50View SolutionIf `x^2 - 3 a x + 14 = 0 " and " x^2 + 2ax - 16 = 0 ` have a common root than `a^4 + a^2` =
03:16View SolutionIf` alpha_1 , alpha_2 ,……….,alpha_n` are the roots of `x^n + px + q = 0 ` , then `(alpha_n - alpha_1) (alpha_n - alpha_2) ………(alpha_n - alpha_(n-1) ) = `
04:22View SolutionAll the roots of the equation
. ` x^5 + 15x^4 + 94x^3 + 305 x^2 + 507 x + 353 = 0` are increased by some real number k in order to eliminate the 4th degree term from the equation. Now, the coefficient of x in the transformed equation is08:17View SolutionThe number of ways in which four letters can be put in four addressed envelops so that no letter goes into envelope meant for it is
03:29View SolutionIf the integer represented by 100! has K consective zeroes at the end, then K =
05:19View SolutionIf n is a positive integer and the coefficient of ` x^10` in the expansion of `(1 + x)^15` is equal to the coefficient of `x^5` in the expansion of `(1-x)^(-n)` then n =
04:37View SolutionIf `x = (2.5)/(3.6) - (2.5.8 )/(3.6.9) (2/5) + (2.5.8.11)/(3.6.12) (2/5)^2 - …… oo` , then ` 7^2 (12 x + 55)^3 = `
View SolutionIf `F_1` and `F_2` are irreducible factors of `x^4 + x^2 + 1 ` with real coefficients and
`(x^3 - 2x^2 + 3x -4)/(x^4 + x^2 + 1) = (Ax + B)/(F_1) + (Cx + D)/(F_2)` , then A + B + C + D =05:13View SolutionThe number of all the possible integral values of `n gt 2` such that `sin (pi)/(2n) + cos (pi)/(2n) = (sqrtn)/(2)` is
View SolutionIf `alpha` and `beta` are angles in the first quadrant sucn than `tan alpha = 1/7` and `sin beta = (1)/(sqrt10)` , then `alpha + 2 beta = `
10:37View Solution`cos (pi/7) cos ((2pi)/(7) ) cos ( (4pi )/(7) ) =`
02:51View SolutionIf `0 lt theta lt pi/2` , the solution of the equation `sin theta - 3 sin 2 theta + sin 3 theta = cos theta - 3 cos 2 theta + cos 3 theta ` is
05:20View Solution`sin^(-1) ( 12/13 ) + cos^(-1) (4/5) + tan^(-1) (63/16) = `
06:52View SolutionIf ` sin h x = 3/4 ` and ` cos h y = 5/3 `, then x + y =
04:31View SolutionIn a `Delta ABC ` , if a = 5 , b = 6, c = 7` , then the length of the median drawn from B is
04:50View SolutionIf `Delta ABC` , if `cot A/2 , cot B/2 : cot C/2 = 4:3:2`, then a : b : c =
04:56View SolutionIf `Delta ABC` if cos A cos B + sin A sin B sin C = 1 and `C = pi/2 ` , then A : B =
02:02View SolutionIf a, b, c are distinct real numbers and P, Q, R are three points whose position vectors are respectively `ahati + b hatj + c hatk , b hati + c hatJ + a hatk` and `c hai + a hatj + b hatk` , then `angle QPR` =
View Solution`Let a = sin^2 x hati + cos^2 x hatj + hatk ,( x in R) ` . If the pairs of vectors a , `hati , a , hatj` and a , `hatk` are adjacent sides of 3 distinct parallelograms and A is the sum of the squares of areas these parallelograms ,then A lies in the interval
View SolutionAssertion (A) a, b, c, d are position vectors of 4 points such that 2a - 3b + 7c -6d = 0 `rArr` a, b, c, d are coplanar.
Reason (R) Vector equation of the plane passing through three points whose position vectors are a, b, c is r = (1-x-y) a + x + yc. Which of the following is true?View SolutionIf |a| = 4, |b| = 5, |a - b| = 3 and `theta ` is the angle between the vectors a and b , then `tan^2 theta` =
03:50View SolutionIf e is unity vector perpendicular to the plane determined by the points ` 2hati + hatj + hatk , hati - hatj + hatk - hatj + hatk` and ` - hati + hatj - hatk ` . If ` a = 2 hati -3 hatj + 6 hatk` , then the projection vector of a on e is
View SolutionIf ` a = 2 hati + j - 3 hatk , b = hati - 2 hatj + 3hatk` ,
`c = - hati + hatj - 4hatk ` and ` d = hati + hatj + 2hatk `, then ` (a xx b) xx ( c xx d) ` =04:34View SolutionThe mean and standard deviation of a distribution of weights of a group of 20 boys are 40 kg and 5 kg respectively. If two boys of weights 43 kg and 37 kg are excluded from this group, then the variance of the distribution of weights of the remaining group of boys is
View SolutionConsider the following data
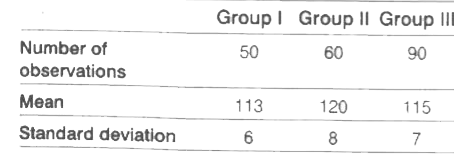
with respect to the consistencies of the above groups , the increasing order of them is03:51View SolutionIn a battery manufacturing factory, machines P, Q and R manufacture 20%, 30% and 50% respectively of the total output. The chances that a defective battery is produced by these machines are 1%, 1.5% and 2% respectively. If a battery is selected as random from production, then the probability that it is defective is
06:11View SolutionSuppose A and B are events of a random experiment such that `P(A) = 1/3 , P (A cap B) = 1/5 ` and` P(A cup B) = 3/5` . Then, match the items of List-I with the items of List-II
 07:15View Solution
07:15View SolutionIn a test, a student either guesses or copies or knows the answer to a multiple choice question with four choices having one correct answer. The probability that he guesses the answer is `1/3` and the probability that he copies it is ` 1/12` . the probability that his answer is correct given that he copied it is `1/6` the probability that he knew the answer, given that he has correctly answered it, is
07:54View SolutionThe probability that a mechanic making an error while using a machine on the nth day is given by `P (E_n) = (1)/(2^n)` If he has operated the machine for 4 days, the probability that he had not made a mistake on 3 of 4 days is
05:36View SolutionIf the probability of a bad reaction from a vaccination is 0.01, then the probability that exactly two out of 300 people will get bad reaction is
02:46View SolutionA(2, 1) and B(1, 2) are two points. If P is a point such that `PA : PB = 2:1`, then the locus of P is
05:17View SolutionFor `a ne b ne c` if the lines x + 2ay + a = 0 , x + 3by + b = 0 and x + 4cy + c = 0 ar concurrent , then a , b, c are in
04:11View SolutionA point moves in the XY-plane such that the sum of its distances from two mutually perpendicular lines is always equal to 3. The area enclosed by the locus of that point is (in sq, units)
03:45View SolutionThe equation of two altitudes of an equilateral triangle are `sqrt3x - y + 8 - 4 sqrt3 = 0 ` and `sqrt3x + y - 12 - 4 sqrt3 = 0` . The equation of the third altitude is
05:47View SolutionIf `P_1, P_2, P_3 ,………, P_n` are n points on the line y = x all lying in the first quadrant, such that `(OP_n) = n (OP_(n-1) ) ` (O is origin ) , `OP_1 = ` and `P_n = (2520 sqrt2 , 2520 sqrt2) `, then n =
View SolutionThe straight line x + y + 1 = 0 bisects an angle between the pair of lines of which one is 2x - 3y + 4 = 0. Then, the equation of the other line is
07:42View SolutionThe combined equation of the pair of straight lines passing through the point of intersection of the pair of lines
` x^2 + 4xy + 3y^2 - 4x - 10y + 3 = 0` and having slopes `1/2` and `- 1/3` is05:49View SolutionIf a circle `C_(1),x^(2)+y^(2)=16` intersects another circle `C_(2)` of radius 5 in such a manner that the common chord is maximum length and has slope `3/4`, then show the centres of `C_(2)` are `(9/5,(-12)/5),((-9)/5,12/5)`
02:42View SolutionThe equation of the circle which touches the circle `x^2 + y^2 - 6x + 6y +17 =0` externally and having the lines `x^2 -3xy -3x + 9y = 0 ` as two normals ,is
05:56View SolutionLet A be the centre of the circle `x^(2)+y^(2)-2x-4y-20=0`. Suppose that the tangent at the points B(1,7) and D(4,-2) on the circle meet at the point C. The area of the quadrilateral ABCD is
08:45View SolutionLet x - 4 = 0 be the radical axis of two circles which are intersecting orthogonally . If `x^2 + y^2 = 36` is one of those circles , then the other circle is
03:20View SolutionThe length of common chord of the circles
`x^2 + y^2 - 6x - 4y + 13 - c^2 = 0` and
` x^2 + y^2 -4x - 6y + 13 -c^2 = 0` is07:13View SolutionIf P is (3, 1) and Q is a point on the curve `y^2 = 8x` , then the locus of the mid-point of the line segment PQ is
03:38View SolutionLet P(2,4), Q(18, -12) be the points on the parabola `y^2 = 8x` . The equation of straight line having slope `1/2` and passing through the point of intersection of the tangents to the parabola drawn at the points P and Q is
05:06View SolutionLet A be a vertex of the ellipse `S = (x^2)/(4) + (y^2)/(9) - 1 = 0` and F be focus of the ellipse `S' = (x^2)/(9) + (y^2)/(4) - 1 = 0` .Let P be a point on the major axis of the ellipse S' = 0 , which divides `bar(OF)` in the ratio 2 : 1 (O is the origin ). If the length of the chord of the ellipse S = 0 through A and P is `(3 sqrt101)/(k) , ` then k =
View SolutionTangents are drawn to the ellipse `(x^2)/(25) + (y^2)/(16) = 1` at all the four ends of its latusrectum. Then, the area (in sq units) of the quadrilateral formed by these tangents is
09:19View SolutionThe lines of the form `xcos phi + ysin phi =P` are chords of the hyperbola `4x^2 - y^2 = 4a^2` which subtend a right angle at the centre of the hyperbola. If these chords touch a circle with centre at (0, 0), then the radius of that circle is
08:46View SolutionLet A(3, 2, - 4) and B(9, 8, -10) be two points. Let` P_1` divide AB in the ratio 1: 2 and `P_2` divide AB in the ratio 2 : 1. If the point `P(alpha, beta, gamma)` divides `P_1P_2` in the ratio 1:1, then` alpha + 2 beta + 2 gamma ` =
07:03View SolutionIf the direction cosines of the two lines satisfy the equations l + m + n = 0,2lm + 2ln - nm = 0, then the acute angle between these lines is
06:36View SolutionIf the equation of the plane passing through the point (2,-1, 3) and perpendicular to the planes 3x - 2y + z = 9 and x + y + z = 9 is x + by + cz + d = 0, then d =
05:58View Solution`lim_(xto a) (sqrt(a + 2x) - sqrt(3a))/(sqrtx - sqrta)`
03:47View SolutionIf a function f(x) defined by
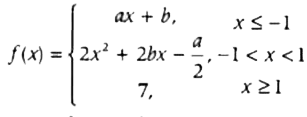 is continous on R, then (a , b) = 05:19View Solution
is continous on R, then (a , b) = 05:19View SolutionThe derivative of `y = (sin x)^(x^2) ` with respect to x is
04:30View SolutionIf `y = ((x + 1)^2 sqrt(x - 1) )/((x + 4)^3 e^x) `, then `(dy)/(dx) = `
04:39View SolutionThe slope of the tangent to the curve `f(x) = tan h^(-1) (sin x) at x = pi `is
03:17View SolutionThe approximate value of
`y = (1.01)^3 + 2(1.01)^(3/2) + 5` is05:59View SolutionIf `y = 2x` is tangent to the curve `y^2 = ax^3 + b` at (1, 2) , then (a, b) =
05:15View SolutionAn angle between the curves `x^2 - y^2 = 4` and `x^2 + y^2 = 4 sqrt2` is
View SolutionLet f(x) be continuous on [0, 4] , differentiable on (0, 4) , f(0) = 4 and f(4) = -2 . If `g(x) =(f(x))/(x + 2)` , then the value of g'(c ) for some Lagrange's constant `c in (0 , 4)` is
02:30View Solution`int( sqrt(tan x) + sqrt(cot x) ) dx = `
04:32View Solution`int(dx)/((2ax + x^2)^(3/2) ) = `
07:32View SolutionIf ` int ( 2dx)/(sqrt(cot^2x - tan^2 x) ) = - sqrt(f(x) ) + c` , then f(x) =
07:20View Solution`int (3^x)/(sqrt(9^x - 1) ) dx = `
02:10View SolutionIf `f(x) = int_1^x (1)/(2 + t^4)` dt ,then
03:31View SolutionIf `I_n = int_(pi//2)^(oo) e^(-x) x dx] ` , then ` (I_(2018) )/(I_(2016)) = `
View SolutionThe area bounded by the curves `y = 2x^2 , y = max {x - [x] + [x]} ` and the lines x = 0, x = 2 (in sq units ), is
View SolutionThe differential equation corresponding to the family of curves given by ` y = a + be^(2x) + ce^(-3x)` is
05:04View SolutionThe general solution of the differential equation `x^2 y dx - (x^3 + y^3) dy = 0` is
07:05View SolutionThe solution of `(1 + y^(2)) dx = (Tan^(-1) y -x) dy` is
03:57View Solution
MATHEMATICS questions and complete solutions for chapter TS EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER (2018) of TS EAMCET PREVIOUS YEAR PAPERS of Class 12
