Complete Solutions to 335(EB) of chapter इंटरमीडिएट परीक्षा, 2018 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | इंटरमीडिएट परीक्षा, 2018 |
| UP BOARD PREVIOUS YEAR | 335(EB) |
| Number Of Questions | 29 |
| Academic Year | 2023-24 |
फलन `2x+3y=sin x`, तो `(dy)/(dx)` का मान ज्ञात कीजिए।
View Solution`int (sec x)/(sec x+tan x)dx` का मान ज्ञात कीजिए।
View Solutionनिम्नलिखित अवकल समीकरण की कोटि एवं घात बताइये- `(d^2y)/(dx^2)=root(4)(y+((dy)/(dx))^2)`
View Solutionकिसी `DeltaABC` को सिद्ध कीजिए की -
`vec(AB)+vec(BC)+vec(CA)=vec0`
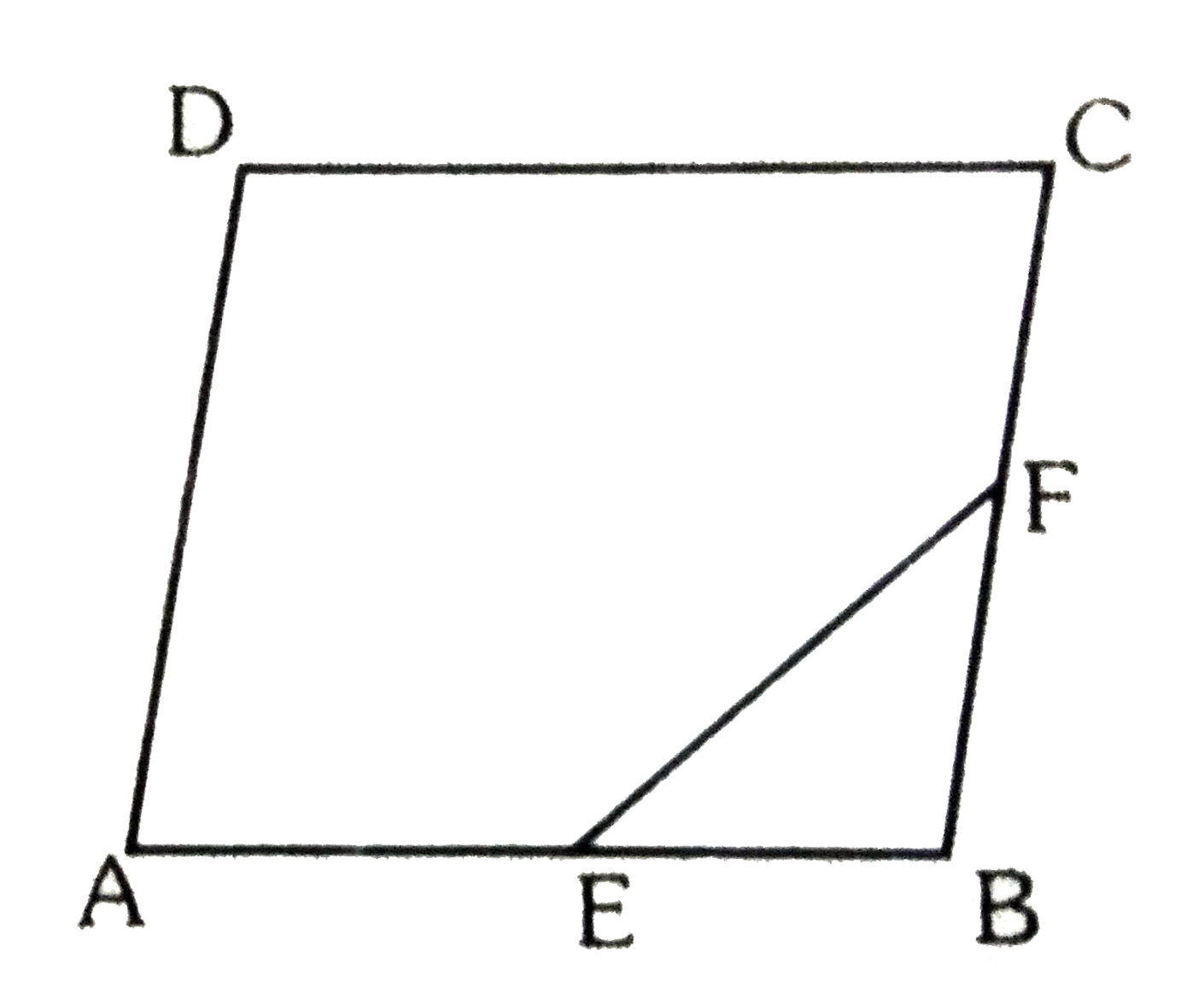
View Solutionपार्श्व चित्र में ABCD एक समान्तर चतुर्भुज है, जिसमे AB तथा BC के मध्य बिन्दु क्रमशः E तथा F है। यदि `vec(AB)=vec(a)` तथा `vec(AD)=vec(b)` तो सदिश `vec(EF)` ज्ञात कीजिये।
View Solutionप्रथम सिद्धान्त से `cos^(-1) x` का अवकल गुणांक ज्ञात कीजिये।
View Solution`int (cos x)/(sin^2 x)dx` का मान ज्ञात कीजिए।
View Solutionयदि `veca =5hati-hatj-3hatk, vecb =hati+3hatj-5hatk` तो दर्शाइए कि सदिश `(veca+vecb)` और `(veca -vecb)` लम्बवत् हैं।
View Solution`int (x^(2) tan^(-1) x^(3))/(1+x^(6)) dx` का मान ज्ञात कीजिए।
View Solutionअवकल समीकरण `(dy)/(dx)=-((1+y^2)/(y))` को हल कीजिए।
View Solutionवक्र `y=x^2-4x-5` के बिन्दु x=-2 पर स्पर्श-रेखा का समीकरण ज्ञात कीजिए।
View Solutionफलन `int(x+1)/(sqrt(x^2+1))dx` का x के सापेक्ष समाकलन ज्ञात कीजिए।
View Solutionअवकल समीकरण `(dy)/(dx)+((1+y^2)/(x))=0` को हल कीजिए।
View Solutionसदिश `5hati-hatj+2hatk` के अनुदिश एक ऐसा सदिश ज्ञात कीजिए जिसका परिमाण 8 इकाई है।
View Solutionएक कण पर तीन बल `2hati + 3hatj +4hatk, hati-4hatj` और `-3hati +hatj-4hatk` लग रहे हैं, सिद्ध कीजिए कि कण सन्तुलन की अवस्था में है।
View Solutionफलन `sin^(-1) 2x sqrt(1-x^2)` का x के सापेक्ष अवकल गुणांक ज्ञात कीजिए।
View Solution`int(dx)/(sqrt(x^2+a^2))` का मान ज्ञात कीजिए।
View Solutionअवकल समीकरण `(dy)/(dx)=(1)/(y+siny)` को हल कीजिए।
View Solutionयदि `vec(OA) = 3hati + 2hatj - hatk` तथा `vec(OB) =hati +3hatj-hatk` हो, तो `Delta` OAB का क्षेत्रफल ज्ञात कीजिए।
View Solutionपरवलय `y^2=16x` के उस अभिलम्ब का समीकरण ज्ञात कीजिए जो x-अक्ष से `60^@` का कोण बनाता है। उस बिन्दु के निर्देशांक भी ज्ञात कीजिए, जहाँ पर यह अभिलम्ब है।
View Solutionएक फल विक्रेता सेब और सन्तरे खरीदने में ₹ 500 की पूँजी लगा सकता है। उसकी दुकान में फलों की केवल 12 पेटियाँ ही रखी जा सकती हैं। सेब की एक पेटी ₹ 50 और सन्तरे की एक पेटी ₹ 25 की आती है। वह सेब की प्रति पेटी ₹ 10 तथा सन्तरे की प्रति पेटी ₹ 6 के लाभ से बेचता है। यह मान कर कि वह खरीदी हुई सभी पेटियों को बेच सकता है, रैखिक प्रोग्रामन द्वारा ज्ञात एक कीजिए कि उसे सेब और सन्तरे की कितनी-कितनी पेटियाँ खरीदनी चाहिए ताकि उसे अधिकतम लाभ हो?
View Solutionसिद्ध कीजिए कि `int_0^(pi//2) (dx)/(1+sqrt(tan x))=pi/4`
View Solutionप्रदर्शित कीजिए कि सदिशों `2hati+hatj +3hatk` और `3hati-2hatj+hatk` के बीच का कोण `60^@` है।
View Solutionदर्शाइए के एक निश्चित आयतन के शंक्वाकार डेरे के बनाने में से काम-से -काम कपड़ा लगेगा जब उसकी ऊंचाई और आधार की त्रिज्या का अनुपात `sqrt(2:1)`है
View Solutionसिद्ध कीजिए कि `underset(0)overset(pi)int (xdx)/(a^(2)cos^(2)x+b^(2)sin^(2)x )=(pi^(2))/(2ab)`
View Solutionमध्यमान प्रमेय सत्यापित कीजिए यदि अंतराल [a,b] में `f(x)= x^(3) - 5x^(2) - 3x,` जहाँ a=1 और b=3 है । `f( c )=0` के लिए ` c in (1,3)` को ज्ञात कीजिए ।
View Solutionपरवलय ` y ^(2) = 4ax ` और सरल रेखा ` y = 2ax ` द्वारा घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए|
View Solutionदर्शाइए की रेखाएं `(x+3)/(-3)=(y-1)/(1)=(z-5)/(5)` तथा `(x+1)/(-1)=(y-2)/(2)=(z-5)/(5)` समतलीय है!
View Solutionग्राफ़िय विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए :
निम्न अवरोधों के अंतर्गत Z = 3x + 4y का अधिकतमीकरण कीजिए :
`x + y le 4, x ge 0, y ge 0`
View Solution
335(EB) questions and complete solutions for chapter इंटरमीडिएट परीक्षा, 2018 of UP BOARD PREVIOUS YEAR of Class 12