Complete Solutions to EXERCISE (COMPREHENSION TYPE PROBLEMS) of chapter APPLICATION OF DERIVATIVES of Class 12 book with complete answers and questions

Let `y = f (x)` such that `xy = x+y +1, x in R-{1} and g (x) =x f (x)`
The minimum value of `g (x)` is:

Let `y = f (x)` such that `xy = x+y +1, x in R-{1} and g (x) =x f (x)`
There exist two values of `x, x_(1) and x _(2)` where `g '(x) =1/2,` then `|x _(1)| + |x_(2)|=`

Let `f (x) = [{:(1-x,,, 0 le x le 1),(0,,, 1 lt x le 2 and g (x) = int_(0)^(x) f (t)dt.),( (2-x)^(2),,, 2 lt x le 3):}`
Let the tangent to the curve `y = g( x)` at point P whose abscissa is `5/2` cuts x-axis in point Q.
Let the prependicular from point Q on x-axis meets the curve `y =g (x)` in point R .Find equation of tangent at to y=g(x) at P .Also the value of
`g (1) =`

Let `f (x) = [{:(1-x,,, 0 le x le 1),(0,,, 1 lt x le 2 and g (x) = int_(0)^(x) f (t)dt.),( (2-x)^(2),,, 2 lt x le 3):}`
Let the tangent to the curve `y = g( x)` at point P whose abscissa is `5/2` cuts x-axis in point Q.
Let the prependicular from point Q on x-axis meets the curve `y =g (x)` in point R .Find equation of tangent at to y=g(x) at P .Also the value of
`g (1) =`

Let `f (x) = [{:(1-x,,, 0 le x le 1),(0,,, 1 lt x le 2 and g (x) = int_(0)^(x) f (t)dt.),( (2-x)^(2),,, 2 lt x le 3):}`
Let the tangent to the curve `y = g( x)` at point P whose abscissa is `5/2` cuts x-axis in point Q.
Let the prependicular from point Q on x-axis meets the curve `y =g (x)` in point R .Find equation of tangent at to y=g(x) at P .Also the value of
`g (1) =`

Let `f(x) lt 0 AA x in (-oo, 0) and f (x) gt 0 ,AA x in (0,oo) ` also `f (0)=0,` Again `f'(x) lt 0 ,AA x in (-oo, -1) and f '(x) gt 0, AA x in (-1,oo)` also `f '(-1)=0` given `lim _(x to -oo) f (x)=0 and lim _(x to oo) f (x)=oo` and function is twice differentiable.
If `f'(x) lt 0 AA x in (0,oo)and f'(0)=1` then number of solutions of equation `f (x)=x ^(2)` is : (a) 1 (b) 2 (c) 3 (d) 4

Let `f(x) lt 0 AA x in (-oo, 0) and f (x) gt 0 ,AA x in (0,oo) ` also `f (0)=0,` Again `f'(x) lt 0 ,AA x in (-oo, -1) and f '(x) gt 0, AA x in (-1,oo)` also `f '(-1)=0` given `lim _(x to -oo) f (x)=0 and lim _(x to oo) f (x)=oo` and function is twice differentiable.
If `f'(x) lt 0 AA x in (0,oo)and f'(0)=1` then number of solutions of equation `f (x)=x ^(2)` is : (a) 1 (b) 2 (c) 3 (d) 4

Let `f(x) lt 0 AA x in (-oo, 0) and f (x) gt 0 AA x in (0,oo) ` also `f (0)=0,` Again `f'(x) lt 0 AA x in (-oo, -1) and f '(x) gt 0 AA x in (-1,oo)` also `f '(-1)=0` given `lim _(x to -oo) f (x)=0 and lim _(x to oo) f (x)=oo` and function is twice differentiable.
The minimum number of points where `f'(x)` is zero is: (a) 1 (b) 2 (c) 3 (d) 4

In the given figure graph of :
`y =p (x) = x ^(n)+a_(1) x ^(n-1) +a_(2) x ^(n-2)+ ….. + a _(n)` is given.

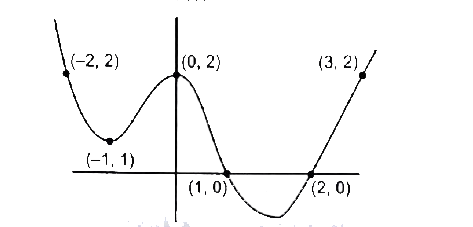
The product of all imaginary roots of `p(x) =0` is:

In the given figure graph of :
`y =p (x) = x ^(n)+a_(1) x ^(n-1) +a_(2) x ^(n-2)+ …..+ a _(n)` is given.

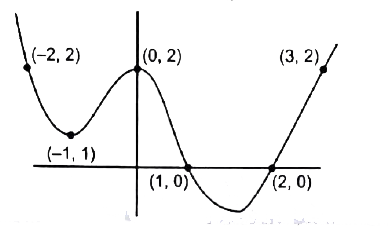
If `p (x) + k=0` has 4 distinct real roots `alpha, beta, gamma,delta ` then`[alpha]+[beta]+[gamma]+[delta],` (where [.] denotes greatest integer function) is equal to:

In the given figure graph of :
`y =p (x) = x ^(n)+a_(1) x ^(n-1) +a_(2) x ^(n-2)+ …..+ a _(n)` is given.

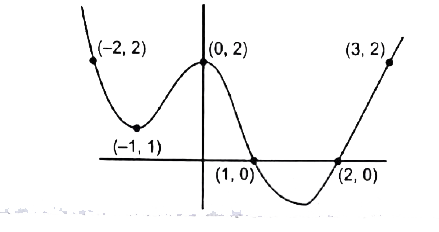
The minimum number of real roots of equation `(p' (x))^(2) +p(x)p''(x) =0` are:

The differentiable function `y= f(x)` has a property that the chord joining any two points `A (x _(1), f (x_(1))) and B (x_(2), f (x _(2)))` always intersects y-axis at `(0,2 x _(1), x _(2)).` Given that `f (1) =-1.` then:
The largest interval in whichy `f (x)` is monotonically increasing, is :

The differentiable function `y= f(x)` has a property that the chord joining any two points `A (x _(1), f (x_(1)) and B (x_(2), f (x _(2)))` always intersects y-axis at `(0,2 x _(1)x _(2)).` Given that `f (1) =-1.` then:
In which of the following intervals, the Rolle's theorem is applicable to the function `F (x) =f (x) + x` ? (a) `[-1,0]` (b) `[0,1]` (c) `[-1,1]` (d) `[0,2]`

about to only mathematics

`If f(x) =x + int_(0)^(1) (xy^(2)+x^(2)y)(f(y)) dy, "find" f(x)` if x and y are independent.