In the given figure graph of :
y=p(x)=xn+a1xn−1+a2xn−2+…..+an is given.
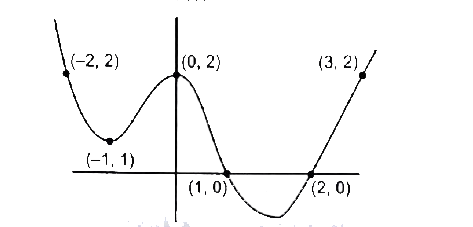
The product of all imaginary roots of p(x)=0 is:
−2
−1
−1/2
noen of these
The correct Answer is:D
Step by step video & image solution for In the given figure graph of : y =p (x) = x ^(n)+a_(1) x ^(n-1) +a_(2) x ^(n-2)+ ….. + a _(n) is given. The product of all imaginary roots of p(x) =0 is: by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPLICATION OF DERIVATIVES BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - EXERCISE (MATHCING TYPE PROBLEMS)
6 Videos
- APPLICATION OF DERIVATIVES BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
22 Videos
- APPLICATION OF DERIVATIVES BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - EXERCISE (ONE OR MORE THAN ANSWER IS/ARE CORRECT )
29 Videos
- AREA UNDER CURVESBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - AREA UNDER CURVESEXERCISE - AXERCISE (SUBJECTIVE TYPE PROBLEMS)
8 Videos
Similar Questions
In the given figure graph of :
y=p(x)=xn+a1xn−1+a2xn−2+…..+an is given.
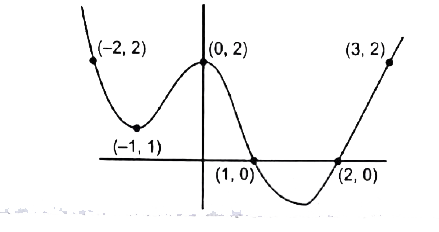
The minimum number of real roots of equation (p'(x))2+p(x)p''(x)=0 are:
View SolutionIn the given figure graph of :
y=p(x)=xn+a1xn−1+a2xn−2+…..+an is given.
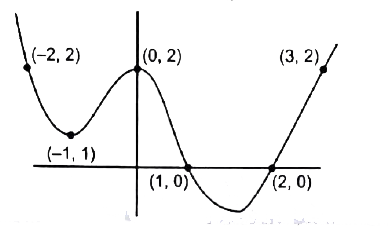
If p(x)+k=0 has 4 distinct real roots α,β,γ,δ then[α]+[β]+[γ]+[δ], (where [.] denotes greatest integer function) is equal to:
View SolutionIn the given figure graph of y=p(x)=x4+ax3+bx2+cx+d is given
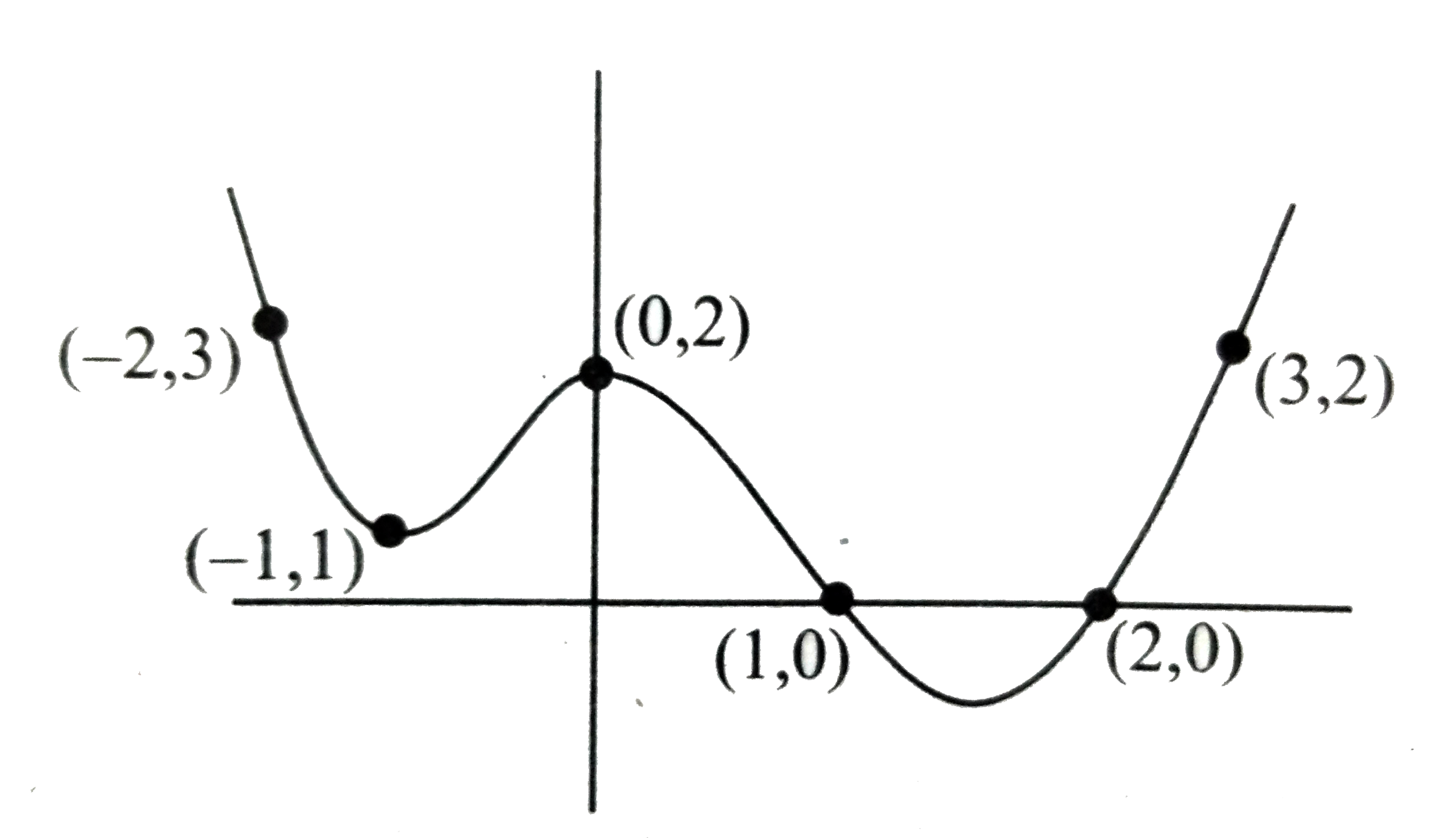
The product of all imaginary roots of p(x)=0 is (a) 1 (b) 2 (c) 13 (d) 14
View SolutionDifferentiate |x|+a0xn+a1xn−1+a2xn−1+...+an−1x+an
View SolutionDifferentiate the following with respect of x:a0xn+a1xn−1+a2xn−2++an−1x+an.
View SolutionIf (1+x+x2+x3)n=a0+a1x+a2x2+………..a3nx3n then which of following are correct
View SolutionLet n be positive integer such that, (1+x+x2)n=a0+a1x+a2x2+….+a2nx2n, then ar is :
View SolutionIf (1+2x+x2)n=2n∑r=0arxr, then ar=
View SolutionFind a1anda9 if an is given by an=n2n+1
View SolutionLet (1+x2)2(1+x)n=a0+a1x+a2x2+… if
a1,a2 and a3 are in A.P , the value of n is
View Solution
