Complete Solutions to Exercise-1 : Single Choice Problems of chapter STRAIGHT LINES of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | STRAIGHT LINES |
| VIKAS GUPTA | Exercise-1 : Single Choice Problems |
| Number Of Questions | 63 |
| Academic Year | 2023-24 |
The ratio in which the line segment joining (2, -3) and (5,6) is divided by the x- axis is :
02:20View SolutionIf is the line whose equation is `ax +by=c.` Let M be the reflection of 'L through the y-axis and let N be the reflection of L through the x-axis. Which of the following must be true about M and N for choices of `a, b` and `c?`
04:04View SolutionFind the values of a for which point (3a,a) lies inside the triangle formed by the lines y=x, the x-axis and line x+y=4.
07:05View SolutionLet m be a positive integer and let the lines ` 13x + 11y = 700 ` and ` y= mx - 1 ` intersect in a point whose coordinates are integer. Then m equals to :
05:05View SolutionIf ` P -= ((1)/(x_(p)), p ), Q = ((1)/(x_(q)),q), R = ((1)/(x_(r)), r)`
where ` x _(k) ne 0 `, denotes the ` k^(th) ` terms of a H.P. for ` k in N `, then :04:35View SolutionIf the sum of the slopes of the lines given by `x^(2)-2cxy-7y^(2)=0` is four times their product , then find the value of c.
02:31View SolutionA piece of cheese is located at (12, 10) in a coordinate plane. A mouse is at (4,-2) and is running up the line ` y= -5x + 18 `. At the point (a, b), the mouse starts getting farther from the cheese rather than closer to it. The value of `(a+b)` is :
05:58View SolutionThe vertex of the right angle of a right angled triangle lies on the straight line `2x +y- 10 =0` and the two other vertices, at points `(2,-3)` and `(4,1)` then the area of triangle in sq. units is-
06:08View SolutionGiven a family of lines a(2x +y+4) + b(x-2y-3)=0 .The number of lines belonging to the family at a distance of `sqrt(10)` from point `(2,-3)` is
04:30View SolutionPoint `(0, beta)` lies on or inside the triangle fromed by the lines ` y=0, x+y=8 ` and ` 3x - 4y + 12 =0`. Then ` beta` can be :
03:35View Solutionthe lines `x + y + 1 = 0; 4x + 3y + 4 = 0` and `x + alphay + beta= 0,` where `alpha^2 + beta^2 = 2,` are concurrent
02:42View Solutionabout to only mathematics
09:32View SolutionIf the points ( 2a, a), (a, 2a) and (a, a) enclose a triangle of area 72 units, then co-ordinates of the centroid of the triangle may be :
04:31View SolutionLet `g(x)= ax + b ` , where ` a lt 0 ` and g is defined from [1,3] onto [0,2] then the value of ` cot ( cos^(-1) (|sin x | + |cos x|) + sin^(-1)(-|cos x | - |sinx|)) ` is equal to :
07:15View SolutionIf any point P is at the equal distances from points A(a+b,a-b) and B(a-b,a+b), then locus of a point is
04:50View SolutionIf the equation `4y^(3) - 8a^(2)yx^(2) - 3ay^(2)x +8x^(3) = 0` represents three straight lines, two of them are perpendicular, then sum of all possible values of a is equal to
02:17View SolutionThe orthocentre of the triangle formed by the lines ` x-7y + 6 =0, 2x - 5y -6 =0` and ` 7x + y -8 =0` is :
06:17View SolutionAll the chords of the curve ` 2x^(2) + 3y^(2) - 5x =0` which subtend a right angle at the origin are concurrent at :
06:48View SolutionPerpendiculars from the point `P(4,4)` to the straight lines `3x+4y+5=0` and `y=mx+7` meet at Q and R, respectively. If the area of triangle PQR is maximum, then the value of is
05:36View Solutionthe equation of two adjacent sides of rhombus are given by `y=x` and `y=7x`. the diagonals of the rhombus intersect each other at point of `(1,2)`.then the area of the rhombus is:
10:09View SolutionThe point P(3, 3) is reflected across the line `y= -x` . Then it is translated horizontally 3 units to the left and vertically 3 units up. Finally, it is reflected across the line `y=x`. What are the coordinates of the point after these transformations ?
05:57View SolutionThe equation `x= t^(3) + 9 ` and ` y= (3t^(3))/(4) + 6` represents a straight line where t is a parameter. Then y- intercept of the line is :
02:21View SolutionThe combined equation of two adjacent sides of a rhombus formed in first quadrant is `7x^2-8xy+y^2=0` then slope of its longer diagonal is
06:45View SolutionThe number of integral point inside the triangle made by the line ` 3x + 4y - 12 =0` with the coordinate axes which are equidistant from at least two sides is/are :
( an integral point is a point both of whose coordinates are integers. )09:54View SolutionThe area of triangle formed by the straight lines whose equations are ` y= 4x + 2, 2y = x + 3 ` and `x=0` is :
07:19View SolutionIn a triangle ABC, if A is `(1, 2)` and the equations of the medians through B and c are `x+ y= 5` and `x= 4` respectively then B must be:
02:18View SolutionThe equation of image of pair of lines y =|x-1|in Y-axis is
02:16View SolutionIf P, Q and R are three points with coordinates `(1, 4), (4, 5) and (m, m)` respectively, then the value of m for which `PR + RQ` is minimum, is :
05:15View SolutionThe vertices of a triangle are `(A(-1,-7),B(5,1),` and `C(1,4)dot` The equation of the bisector of `/_A B C` is____
04:34View SolutionIf one of the lines given by `6x^2- xy +4cy^2=0` is `3x +4y=0`, then `c=`
04:34View SolutionLines `L_1` and `L_2` have slopes m and n, respectively, suppose `L_1` makes twice as large angle with the horizontal (mesured counter clockwise from the positive x-axis as does `L_2` and `L_1` has 4 times the slope of `L_2`. If `L_1` is not horizontal, then the value of the proudct mn equals.
03:33View SolutionGiven A(0,0) and B(x,y) wih `x in (0,1) " and " y gt 0`. Let the slope of line AB be `m_(1), "where" 0 lt m_(2) lt m_(1)`. If the are of triangle ABC can be expresses as `(m_(1) - m_(2)) f (x).` then the largest possible value of `f(x)` is
07:01View SolutionIf `a , b ,c` are in harmonic progression, then the straight line `((x/a))_(y/b)+(l/c)=0` always passes through a fixed point. Find that point.
01:51View Solutionif `X^2/a+y^2/b+(2xy)/h=0` represent pair of straight lies and slope one line is twice the other line then `ab:h^2`.
04:34View SolutionStatement-1: variable line drawn through a fixed point cuts the coordinate axes at A and B. The locus of mid-point of AB is a circle. because Statement 2: Through 3 non-collinear points in a plane, only one circle can be drawn.
02:16View SolutionA line passing through origin and is perpendicular to two given lines `2x+y+6=0` and `4x+2y-9=0`. The ratio in which the origin divides this line is (a) ` 1 : 2 ` (b) ` 1 : 1 ` (c) ` 5 : 4` (d) ` 3 : 4 `
06:08View SolutionIf a vertex of a triangle is (1, 1) and the mid-points of two side through this vertex are (-1, 2) and (3, 2), then centroid of the triangle is
03:26View Solutionabout to only mathematics
02:23View SolutionFind all points on the line `x+y=4` that lie at a unit distance from the line `4x+3y=10`.
05:39View SolutionThe orthocentre of the triangle formed by the lines ` x + y =1 , 2x + 3y =6 ` and ` 4x - y +4 =0` lies in :
09:55View SolutionThe equation of the line passing through the intersection of the lines ` 3x + 4y = -5, 4x + 6y = 6 ` and perpendicular to ` 7x - 5y + 3 = 0 ` is :
03:52View SolutionThe point (2, 1), (8, 5) and (x, 7) lie on a straight line. Then the value of x is :
03:20View SolutionIn a parallelogram PQRS (taken in order), P is the point (-1, -1), Q is (8, 0) and R is (7, 5). Then S is the point :
03:56View SolutionThe area of triangle whose vertices are ` (a, a), (a + 1, a + 1), (a+2, a)` is :
02:53View SolutionThe equation ` x^(2) + y^(2) - 2xy -1 =0 ` represents :
01:58View SolutionLet A (-2, 0) and B(2, 0), then the number of integral values of a, `a in [-10, 10] for which line segment AB subtends an acute angle at point C (a, a+1) is
06:58View SolutionThe angle between sides of a rhombus whose v2 times sides is mean of its two diagonal, is equal to:`a)30^@ (b) 45^@ (c) 60^@(d) 90^@`
04:57View SolutionA rod of AB of length 3 rests on a wall as follows :
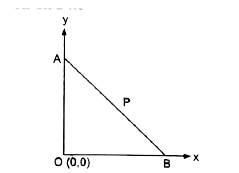
P is a point on AB such that ` AP : PB = 1 : 2 ` If the rod slides along the wall, then the locus of P lies on04:47View SolutionIf ` (x^(2))/(a) + (y^(2))/(b) + (2xy)/(h) =0` represent pair of straight lines and slope of one line is twice the other, then ` ab : h^(2) ` is :
04:34View Solutionlocus of point of reflection of point `(a,0)` w.r.t. the line `yt=x+at^2` is given by:
02:56View SolutionA light ray emerging from the point source placed at `P(1,3)` is reflected at a point Q in the axis of x. If the reflected ray passes through the point `R(6, 7)`, then the abscissa of Q is:
04:00View Solutionif the axes are rotated through 60 in the anticlockwise sense,find the transformed form of the equation `x^2-y^2=a^2`,
06:02View Solutionabout to only mathematics
06:22View Solutionif m and b are real numbers and `mbgt0`, then the line whose equation is `y=mx+b` cannot contain the point
05:13View SolutionThe number of possible straight lines passing through `(2,3)` and forming a triangle with the coordinate axes, whose area is 12 sq. units, is one (b) two (c) three (d) four
05:03View SolutionIf `x_1,x_2,x_3` as well as `y_1,y_2,y_3` are in `G P` with the same common ratio, then the points `(x_1,y_1),(x_2,y_2),` and `(x_3, y_3)dot` (a)lie on a straight line (b)lie on an ellipse (c)lie on a circle (d) are the vertices of a triangle.
03:20View SolutionProve that the locus of the centroid of the triangle whose vertices are `(acost ,asint),(bsint ,-bcost),` and `(1,0)` , where `t` is a parameter, is circle.
05:11View SolutionFind the equation of the straight line passing through the point (4,3) and making intercepts on the coordinate axes whose sum is -1.
04:28View SolutionLet ` A -= (3, 2) ` and ` B-= (5, 1) ` . ABP is an equilateral triangle is constructed one the side of AB remote from the origin then the orthocentre of triangle ABP is :
10:05View SolutionArea of the triangle formed by the lines through point (6, 0) and at a perpendicular distance of 5 from point (1, 3) and line ` y = 16 ` in square units is :
10:11View SolutionThe orthocentre of the triangle with vertices `(5, 0),(0, 0), ((5)/(2), (5sqrt(3))/(2))` is :
04:31View SolutionShow that all chords of the curve `3x^2-y^2-2x+4y=0,` which subtend a right angle at the origin, pass through a fixed point. Find the coordinates of the point.
04:16View SolutionLet `P-=(-1,0),Q-=(0,0), "and " R-=(3,3sqrt(3)) " be three points".`
Then the equation of the bisector of `angle PQR` is05:58View Solution
Exercise-1 : Single Choice Problems questions and complete solutions for chapter STRAIGHT LINES of SHRI BALAJI MATHS (ENGLISH) of Class 12
