If is the line whose equation is ax+by=c. Let M be the reflection of 'L through the y-axis and let N be the reflection of L through the x-axis. Which of the following must be true about M and N for choices of a,b and c?
The x- intercepts of M and N are equal
The y- intercepts of M and N are equal
The slopes of M and N are equal
The slopes of M and N are reciprocal
The correct Answer is:C
To solve the problem, we need to find the equations of the lines M and N, which are the reflections of the line L given by the equation ax+by=c through the y-axis and x-axis, respectively.
Step 1: Write the equation of line L
The equation of line L is given as:
ax+by=c
Step 2: Find the reflection of line L through the y-axis (line M)
When a line is reflected through the y-axis, the x-coefficient changes sign. Therefore, the equation of line M will be:
−ax+by=c
This can be rewritten as:
−ax+by−c=0
Step 3: Find the reflection of line L through the x-axis (line N)
When a line is reflected through the x-axis, the y-coefficient changes sign. Therefore, the equation of line N will be:
ax−by=c
This can be rewritten as:
ax−by−c=0
Step 4: Determine the slopes of lines M and N
To find the slopes of lines M and N, we can rearrange their equations into slope-intercept form y=mx+b.
For line M:
by=ax+c⟹y=abx+cb
So, the slope of line M is:
mM=ab
For line N:
−by=−ax+c⟹y=abx−cb
So, the slope of line N is:
mN=ab
Step 5: Conclusion about the slopes of M and N
Since both lines M and N have the same slope:
mM=mN=ab
This means that the slopes of lines M and N are equal.
Final Answer
The statement that must be true about lines M and N is that they have the same slope.
---
The equation of line L is given as:
ax+by=c
When a line is reflected through the y-axis, the x-coefficient changes sign. Therefore, the equation of line M will be:
−ax+by=c
This can be rewritten as:
−ax+by−c=0
When a line is reflected through the x-axis, the y-coefficient changes sign. Therefore, the equation of line N will be:
ax−by=c
This can be rewritten as:
ax−by−c=0
To find the slopes of lines M and N, we can rearrange their equations into slope-intercept form y=mx+b.
by=ax+c⟹y=abx+cb
So, the slope of line M is:
mM=ab
−by=−ax+c⟹y=abx−cb
So, the slope of line N is:
mN=ab
Since both lines M and N have the same slope:
mM=mN=ab
This means that the slopes of lines M and N are equal.
The statement that must be true about lines M and N is that they have the same slope.
Topper's Solved these Questions
- STRAIGHT LINES BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - STRAIGHT LINES EXERCISE - Exercise-2 : One or More than One Answer is/are Correct
12 Videos
- STRAIGHT LINES BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - STRAIGHT LINES EXERCISE - Exercise-3 : Comprehension Type Problems
4 Videos
- SOLUTION OF TRIANGLESBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-5 : Subjective Type Problems
11 Videos
- TRIGONOMETRIC EQUATIONS BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONS EXERCISE - Exercise-5 : Subjective Type Problems
9 Videos
Similar Questions
Let P be the point (3, 2). Let Q be the reflection of P about the x-axis. Let R be the reflection of Q about the line y=−x and let S be the reflection of R through the origin, PQRS is a convex quadrilateral . Find the area of PQRS.
View SolutionLet m,n are integers with 0<n<m. A is the point (m,n) on the Cartesian plane. B is the reflection of A in the line y=x. C is the reflection of B in the y-axis, D is the reflection of C in the x-axis and E is the reflection of D in the y-axis. The area of the pentagon ABCDE is
a.2m(m+n) b. m(m+3n) c. m(2m+3n) d. 2m(m+3n)
View Solution
Knowledge Check
In the figure, lines l, m and n intersect at O. Which one of the following must be true about the value of a?
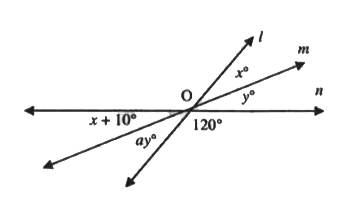 Aa<5/8Ba=5/7Ca=5/6Da=1
Aa<5/8Ba=5/7Ca=5/6Da=1Which equation represents the line that is the reflection of the line y=2x−3 in the y-axis?
Ay=−2x−3By=−2x+3Cy=2x+3Dy=3x−2Let m and n be 2 positive integers, such that m<n. Which of the following compound inequalities must be true?
A0<√mn<mB1<√mn<mCm<√mn<nD√m<√mn<√n
Let m,n are integers with 0<n<m. A is the point (m,n) on the Cartesian plane. B is the reflection of A in the line y=x. C is the reflection of B in the y-axis. D, is the reflection of C in the x-axis and E is the reflection of D in the y-axis. The area of the pentagon ABCDE is 2m(m+n) (b) m(m+3n) m(2m+3n) (d) 2m(m+3n)
View SolutionConsider a point A(m,n) , where m and n are positve intergers. B is the reflection of A in the line y=x, C is the reflaction of B in the y axis, D is the reflection of C in the x axis and E is the reflection of D is the y axis. The area of the pentagon ABCDE is a. 2m(m+n) b. m(m+3n) c. m(2m+3n) d. 2m(m+3n)
View SolutionThe equations to the straight line through (a,b,c) parallel to the z-axis are
View SolutionFind the equation of the straight line which passes through
the origin and the point of intersection of the lines ax+by+c=0anda'x+b'y+c'=0.
View SolutionFind the equation of the straight line through the point (α,β) and perpendiculasr to the line lx+my+n=0.
View Solution
