Complete Solutions to Exercise-1 : Single Choice Problems of chapter STRAIGHT LINES of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | STRAIGHT LINES |
| VK JAISWAL | Exercise-1 : Single Choice Problems |
| Number Of Questions | 63 |
| Academic Year | 2023-24 |
The ratio in which the line segment joining (2, -3) and (5,6) is divided by the x- axis is :
View SolutionIf is the line whose equation is `ax +by=c.` Let M be the reflection of 'L through the y-axis and let N be the reflection of L through the x-axis. Which of the following must be true about M and N for choices of `a, b` and `c?`
View SolutionThe complete set of real values of 'a' such that the point lies triangle `p(a, sin a)` lies inside the triangle formed by the lines `x-2y +2= 0; x+y=0` and `x-y-pi=0`
View SolutionLet m be a positive integer and let the lines ` 13x + 11y = 700 ` and ` y= mx - 1 ` intersect in a point whose coordinates are integer. Then m equals to :
View SolutionIf ` P -= ((1)/(x_(p)), p ), Q = ((1)/(x_(q)),q), R = ((1)/(x_(r)), r)`
where ` x _(k) ne 0 `, denotes the ` k^(th) ` terms of a H.P. for ` k in N `, then :
View SolutionIf the sum of the slopes of the lines given by `x^(2)+2cxy-y^(2)=0` is four times their product, then c has the value
View SolutionA piece of cheese is located at (12, 10) in a coordinate plane. A mouse is at (4,-2) and is running up the line ` y= -5x + 18 `. At the point (a, b), the mouse starts getting farther from the cheese rather than closer to it. The value of `(a+b)` is :
View SolutionThe vertex of the right angle of a right angled triangle lies on the straight line `2x -y- 10 =0` and the two other vertices, at points `(2,-3)` and `(4,1)` then the area of triangle in sq. units is-
View SolutionGiven a family of lines a(2x +y+4) + b(x-2y-3)=0 .The number of lines belonging to the family at a distance of `sqrt(10)` from point `(2,-3)` is
View SolutionPoint `(0, beta)` lies on or inside the triangle fromed by the lines ` y=0, x+y=8 ` and ` 3x - 4y + 12 =0`. Then ` beta` can be :
View Solutionthe lines `x + y + 1 = 0; 4x + 3y + 4 = 0` and `x + alphay + beta= 0,` where `alpha^2 + beta^2 = 2,` are concurrent
View SolutionA straight line through the origin o meets the parallel lines `4x+2y= 9` and `2x +y+ 6=0` points P and Q respectively. Then the point o divides the segment PQ in the ratio: : (A) 1:2 (B) 3:2 (C) 2:1 D) 4:3
View SolutionIf the points ( 2a, a), (a, 2a) and (a, a) enclose a triangle of area 72 units, then co-ordinates of the centroid of the triangle may be :
View SolutionLet `g(x)= ax + b ` , where ` a lt 0 ` and g is defined from [1,3] onto [0,2] then the value of ` cot ( cos^(-1) (|sin x | + |cos x|) + sin^(-1)(-|cos x | - |sinx|)) ` is equal to :
View SolutionIf the point P(x, y) be equidistant from the points `A(a+b, a-b)` and `B(a-b, a+b)` then
View SolutionIf the equation `4y^(3) - 8a^(2)yx^(2) - 3ay^(2)x +8x^(3) = 0` represents three straight lines, two of them are perpendicular, then sum of all possible values of a is equal to
View SolutionThe orthocentre of the triangle formed by the lines `x - 7y + 6 = 0, 2x - 5y - 6 = 0 and 7x + y - 8 = 0` is
View SolutionAll the chords of the curve ` 2x^(2) + 3y^(2) - 5x =0` which subtend a right angle at the origin are concurrent at :
View SolutionFrom a point` P=(3, 4)` perpendiculars `PQ` and `PR` are drawn to line `3x +4y -7=0` and a variable line `y -1= m (x-7)` respectively then maximum area of triangle `PQR` is :
View Solutionthe equation of two adjacent sides of rhombus are given by `y=x` and `y=7x`. the diagonals of the rhombus intersect each other at point of `(1,2)`.then the area of the rhombus is:
View SolutionThe point P(3, 3) is reflected across the line `y= -x` . Then it is translated horizontally 3 units to the left and vertically 3 units up. Finally, it is reflected across the line `y=x`. What are the coordinates of the point after these transformations ?
View SolutionThe equation `x= t^(3) + 9 ` and ` y= (3t^(3))/(4) + 6` represents a straight line where t is a parameter. Then y- intercept of the line is :
View SolutionThe combined equation of two adjacent sides of a rhombus formed in first quadrant is `7x^2-8xy+y^2=0` then slope of its longer diagonal is
View SolutionThe number of integral point inside the triangle made by the line ` 3x + 4y - 12 =0` with the coordinate axes which are equidistant from at least two sides is/are :
( an integral point is a point both of whose coordinates are integers. )
View SolutionThe area of triangle formed by the straight lines whose equations are ` y= 4x + 2, 2y = x + 3 ` and `x=0` is :
View Solutionin a triangle ABC, if A is `(1, 2)` and the equations of the medians through B and c are `x+ y= 5` and `x= 4` respectively then B must be:
View SolutionThe equation of image of pair of lines `y=|x-1|` with respect to y-axis is :
View SolutionIf P, Q and R are three points with coordinates `(1, 4), (4, 5) and (m, m)` respectively, then the value of m for which `PR + RQ` is minimum, is :
View SolutionThe vertices of a triangle are `A (-1, -7), B (5, 1) and C(1, 4)`. The equation of the bisector of the angle ABC
View SolutionIf one of the lines given by `6x^2- xy +4cy^2=0` is `3x +4y=0`, then `c=`
View SolutionThe equations of `L_1 and L_2` are `y = mx and y = nx,` respectively. Suppose `L_1` make twice as large of an angle with the horizontal (measured counterclockwise from the positive x-axis) as does `L_2` and that `L_1` has 4 times the slope of `L_2.` If `L_1` is not horizontal, then the value of the product `(mn)` equals:
View SolutionGiven `A (0, 0)` and `B (x,y)`with `x epsilon (0,1)` and `y>0`. Let the slope of the line AB equals `m_1` Point C lies on the line `x= 1` such that the slope of BC equals `m_2` where `0< m_2< m_1` If the area of the triangle ABC can expressed as `(m_1- m_2)f(x)`, then largest possible value of `f(x)` is:
View SolutionIf a,b,c are in H.P., then the straight line `(x)/(a) + (y)/(b) + (1)/(c )` = 0 always passes through a fixed point and that point is
View Solutionif `X^2/a+y^2/b+(2xy)/h=0` represent pair of straight lies and slope one line is twice the other line then `ab:h^2`.
View SolutionStatement-1: variable line drawn through a fixed point cuts the coordinate axes at A and B. The locus of mid-point of AB is a circle. because Statement 2: Through 3 non-collinear points in a plane, only one circle can be drawn.
View SolutionA line passing through origin and is perpendicular to two given lines `2x+y+6=0` and `4x+2y-9=0`. The ratio in which the origin divides this line is
View SolutionIf a vertex of a triangle is (1, 1) and the mid-points of two side through this vertex are (-1, 2) and (3, 2), then centroid of the triangle is
View Solutionthe diagonals of the parallelogram PQRS are along the lines `x+3y=4` and `6x-2y=7` then PQRS is must be:
View SolutionThe two points on the line `x+y=4` that lies at a unit perpendicular distance from the line `4x+3y=10` are `(a_(1), b_(1))` and `(a_(2), b_(2))` then `a_(1)+b_(1)+a_(2)+b_(2)` is equal to
View SolutionThe orthocenter of the triangle formed by lines ` x + y = 1, 2x + 3y =6 and 4x -y +4 =0 ` lines in quadrant number
View SolutionThe equation of the line passing through the intersection of the lines ` 3x + 4y = -5, 4x + 6y = 6 ` and perpendicular to ` 7x - 5y + 3 = 0 ` is :
View SolutionThe point (2, 1), (8, 5) and (x, 7) lie on a straight line. Then the value of x is :
View SolutionIn a parallelogram PQRS (taken in order), P is the point (-1, -1), Q is (8, 0) and R is (7, 5). Then S is the point :
View SolutionThe area of triangle whose vertices are ` (a, a), (a + 1, a + 1), (a+2, a)` is :
View SolutionThe equation ` x^(2) + y^(2) - 2xy -1 =0 ` represents :
View SolutionLet A (-2, 0) and B(2, 0), then the number of integral values of a, `a in [-10, 10] for which line segment AB subtends an acute angle at point C (a, a+1) is
View SolutionThe angle between sides of a rhombus whose v2 times sides is mean of its two diagonal, is equal to:`a)30^@ (b) 45^@ (c) 60^@(d) 90^@`
View SolutionA rod of AB of length 3 rests on a wall as follows :
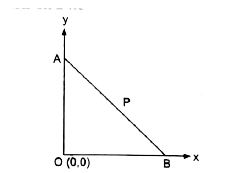
P is a point on AB such that ` AP : PB = 1 : 2 ` If the rod slides along the wall, then the locus of P lies on
View Solutionif `X^2/a+y^2/b+(2xy)/h=0` represent pair of straight lies and slope one line is twice the other line then `ab:h^2`.
View Solutionlocus of point of reflection of point `(a,0)` w.r.t. the line `yt=x+at^2` is given by:
View SolutionA light ray emerging from the point source placed at `P(1,3)` is reflected at a point Q in the axis of x. If the reflected ray passes through the point `R(6, 7)`, then the abscissa of Q is:
View Solutionif the axes are rotated through 60 in the anticlockwise sense,find the transformed form of the equation `x^2-y^2=a^2`,
View SolutionThe straight lines `3x+y-4=0,x+3y-4=0` and `x+y=0` form a triangle which is :
View Solutionif m and b are real numbers and `mbgt0`, then the line whose equation is `y=mx+b` cannot contain the point
View SolutionThe number of possible straight lines passing through point(2,3) and forming a triangle with coordiante axes whose area is 12 sq. unit is: a. one b. two c. three d. four
View SolutionIf `x_1,x_2, x_3` and `y_1, y_ 2, y_3 `are both in `G.P.` with the same common ratio then the points `(x_1,y_1), (x_2, y_2) and (x_3, y_3)`
View SolutionLocus of centroid of the triangle whose vertices are (a cos t, a sin t), (b sin t, - b cos t) and (1, 0), where is a
View SolutionThe equation of the straight line passing through the point (4, 3) and making intercepts on the co-ordinate axes whose sum is -1 is
View SolutionLet A `(3, 2)` and B `(5,1)`. ABP is an equilateral triangle is constructed one the side of AB remote from the origin then the orthocentre of triangle ABP is:
View SolutionArea of the triangle formed by the lines through point (6, 0) and at a perpendicular distance of 5 from point (1, 3) and line ` y = 16 ` in square units is :
View SolutionThe orthocentre of the triangle with vertices `(5, 0),(0, 0), ((5)/(2), (5sqrt(3))/(2))` is :
View SolutionAll chords of the curve `3x^2-y^2-2x+4y=0` which subtend a right angle at the origin, pass through the fixed point
View SolutionLet `P(-1,0), Q(0,0),R(3,3sqrt(3))` be three points then the equation of the bisector of the angle `anglePQR` is :
View Solution
Exercise-1 : Single Choice Problems questions and complete solutions for chapter STRAIGHT LINES of VK JAISWAL MATHS (HINGLISH) of Class 12