Complete Solutions to Exercise-1 : Single Choice Problems of chapter SOLUTION OF TRIANGLES of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | SOLUTION OF TRIANGLES |
| VK JAISWAL | Exercise-1 : Single Choice Problems |
| Number Of Questions | 59 |
| Academic Year | 2023-24 |
In a `Delta ABC` if `9 (a^2 + b^2) = 17c^2` then the value of the `(cot A + cot B) / cotC` is
View SolutionLet H be the orthocenter of triangle ABC, then angle subtended by side BC at the centre of incircle of `DeltaCHB` is :
View SolutionCircum radius of a `DeltaABC` is 3 units, let O be the circum and H be the orthocentre then the value of `(1)/(64)(AH^(2)+BC^(2))(BH^(2)+AC^(2))(CH^(2)+AB^(2))` equals :
View SolutionThe angles A, B and C of a triangle ABC are in arithmetic progression. If `2b^(2)+3c^(2)` then the angle A is :
View SolutionIn a triangle ABC if `tan.(A)/(2)tan.(B)/(2)=(1)/(3)` and ab = 4, then the value of c can be
View SolutionIn a triangle ABC the expression `acosBcosC+bcosC cosA+c cosA cosB` equals to :
View SolutionThe set of all real numbers `a` such that `a^2+2a ,2a+3,a n da^2+3a+8` are the sides of a triangle is_____
View SolutionIn a `DeltaABC, angleB=(pi)/(3) and angleC=(pi)/(4)` let D divide BC internally in the ratio `1:3`, then ` (sin(angleBAD))/(sin(angleCAD))` is equal to :
View SolutionLet AD, BE, CF be the lengths of internal bisectors of angles A, B, C respectively of triangle ABC. Then the harmonic mean of `AD"sec"(A)/(2),BE"sec"(B)/(2),CF"sec"(C )/(2)` is equal to :
View SolutionIn a triangle ABC, if `2b=a+c` and `A-C=90`, then `sin B` equals
View SolutionIn a triangle ABC, if `2a cos ((B-C)/(2))=b+c`, then secA is equal to :
View SolutionIn a triangle `A B CifB C=1a n dA C=2,` then what is the maximum possible value of angle `A ?`
View Solution`Delta I_(1)I_(2)I_(3)` is an excentral triangle of an equilateral triangle `Delta ABC` such that `I_(1)I_(2)=4` unit, if `DeltaDEF` is pedal triangle of `DeltaABC`, then `(Ar(Delta I_(1)I_(2)I_(3)))/(Ar (DeltaDEF))=`
View SolutionLet ABC be a triangle with `angleBAC = 2pi//3 and AB = x` such that (AB) (AC) = 1. If x varies, then find the longest possible length of the angle bisector AD
View SolutionIn a equilateral triangle r, R and `r_(1)` form (where symbols used have usual meaning)
View SolutionIn `DeltaABC` if `(sinA)/(sinC)=(sin(A-B))/(sin(B-C))`, then `a^(2), b^(2), c^(2)` are in :
View SolutionIn `DeltaABC, tanA=2, tanB=(3)/(2) and c=sqrt(65)`, then circumradius of the triangle is :
View SolutionIf the sides a, b, c of a triangle ABC are the roots of the equation `x^(3)-13x^(2)+54x-72=0`, then the value of `(cosA)/(a)+(cosB)/(b)+(cosC)/(c )` is equal to :
View SolutionIn `DeltaABC," if " angleC=90^(@)," then " (a+c)/(b)+(b+c)/(a)` is equal to :
View SolutionIn a `DeltaABC," if " a^(2)sinB=b^(2)+c^(2)`, then :
View SolutionIf R and R' are the circumradii of triangles ABC and OBC, where O is the orthocenter of triangle ABC, then :
View SolutionThe acute angle of a rhombus whose side is a mean proportional between its diagonals is
View SolutionIn a `DeltaABC` right angled at A, a line is drawn through A to meet BC at D dividing BC in `2:1`. If `tan(angleADC)=3` then `angleBAD` is :
View SolutionA circle is cirumscribed in an equilateral triangle of side `'l'`. The area of any square inscribed in the circle is :
View Solutionif the sides of a triangle are in the ratio `2:sqrt6 : sqrt3 + 1, `then the largest ange of the trangle will be (1) 60 (3) 90 (2) 75 (4) 120
View SolutionIn a triangle ABC if a, b, c are in A.P. and `C-P=120^(@)`, then `(s)/(r )=`
(where notations have their usual meaning)
View SolutionIf in `DeltaABC, a = 5, b = 4 and cos (A - B) = 31/32`, then
View SolutionIf semiperimeter of a triangle is 15, then the value of `(b+c)cos(B+C)+(c+a)cos(C+A)+(a+b)cos(A+B)` is equal to :
(where symbols used have usual meanings)
View SolutionLet triangle ABC be an isosceles with AB=AC. Suppose that the angle bisector of its angle B meets the side AC at a point D and that `BC=BD+AD`. Measure of the angle A in degrees, is :
View SolutionIn triangle ABC if `A:B:C=1:2:4," then " (a^(2)-b^(2))(b^(2)-c^(2))(c^(2)-a^(2))=lambda a^(2)b^(2)c^(2)`, where `lambda=`
(where notations have their usual meaning)
View SolutionIn a triangle ABC with altitude AD, `angleBAC=45^(@), DB=3 and CD=2`. The area of the triangle ABC is :
View SolutionA triangle has base 10 cm long and the base angles of `50^(@) and 70^(@)`. If the perimeter of the triangle is `x+y cos z^(@)` where `z in (0, 90)` then the value of `x+y+z` equals :
View SolutionLet H be the orthocenter of triangle ABC, then angle subtended by side BC at the centre of incircle of `DeltaCHB` is :
View SolutionTriangle ABC is right angle at A. The points P and Q are on hypotenuse BC such that `BP = PQ = QC`.if `AP = 3 and AQ = 4`, then length BC is equal to
View SolutionIn a `DeltaABC` if `b =a (sqrt3-1) and /_C =30^@` then the measure of the angle A is
View SolutionThrough the centroid of an equilateral triangle, a line parallel to the base is drawn. On this line, an arbitrary point P is taken inside the triangle. Let h denote the perpendicular distance of P from the base of the triangle. Let `h_(1) and h_(2)` be the perpendicular distance of P from the other two sides of the triangle . Then :
View SolutionThe angles A, B and C of a triangle ABC are in arithmetic progression. AB=6 and BC=7. Then AC is :
View SolutionIn `DeltaABC," if " A-B=120^(@) and R=8r`, then the value of `(1+cosC)/(1-cosC)` equals :
(All symbols used hav their usual meaning in a triangle)
View SolutionThe lengths of the sides CB and CA of a triangle ABC are given by a and b and the angle C is `(2pi)/(3)`. The line CD bisects the angle C and meets AB at D. Then the length of CD is :
View SolutionIn `Delta ABC`, angle A is `120^(@), BC + CA = 20, and AB + BC = 21` Find the length of the side BC
View SolutionA triangle has sides 6,7, and 8. The line through its incenter parallel to the shortest side is drawn to meet the other two sides at P and Q. Then find the length of the segment PQ.
View SolutionThe perimeter of a `DeltaABC` is 48 cm and one side is 20 cm. Then remaining sides of `DeltaABC` must be greater than :
View SolutionIn a equilateral triangle r, R and `r_(1)` form (where symbols used have usual meaning)
View SolutionThe expression `((a+b+c)(b+c-a)(c+a-b)(a+b-c))/(4b^(2)c^(2))` is equal to :
View SolutionCircumradius of an isosceles `DeltaABC` with `angleA=angleB` is 4 times its in radius, then cosA is root of the equation :
View SolutionA is the orthocentre of `DeltaABC` and D is reflection point of A w.r.t. perpendicualr bisector of BC, then orthocenter of `DeltaDBC` is :
View SolutionIf `a ne b ne c` are all positive, then the value of the determinant `|{:(a,b,c),(b,c,a),(c,a,b):}|`is
View SolutionIn triangle ABC if `A:B:C=1:2:4," then " (a^(2)-b^(2))(b^(2)-c^(2))(c^(2)-a^(2))=lambda a^(2)b^(2)c^(2)`, where `lambda=`
(where notations have their usual meaning)
View SolutionIn any triangle, the minimum value of `r_(1) r_(2) r_(3) //r^(3)` is equal to
View SolutionIn `DeltaABC, a = 3, b = 4` and `c = 5`, then value of `sinA + sin2B + sin3C` is
View SolutionIn any triangle ABC, the value of `(r_(1)+r_(2))/(1+cosC)` is equal to (where notation have their usual meaning) :
View SolutionIn a `!ABC` , medians AD and BE are drawn. If AD = 4, `angleDAB=pi//6` and `angleABE=pi//3` then the area of `!ABC` is
View SolutionThe sides of the triangle are sin`alpha` , cos`alpha` and `sqrt(1+sinalphacosalpha)` for some `0 lt alpha lt (pi)/2`. Then the greatest angle of the triangle is
View SolutionLet ABC be a right with `angleBAC=(pi)/(2)`, then `((r^(2))/(2R^(2))+(r )/(R ))` is equal to :
(where symbols used have usual meaning in a striangle)
View SolutionFind the radius of the circle escribed to the triangle ABC (Shown in the figure below) on the side BC if `angleNAB=30^(@), angleBAC=30^(@), AB=AC=5`.
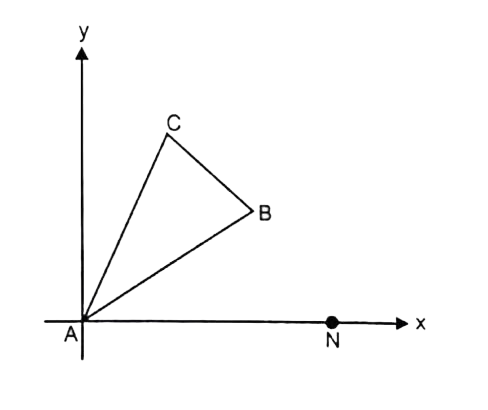
View SolutionIn a `DeltaABC`, with usual notations, if `b gt c` then distance between foot of median and foot of altitude both drawn from vertex A on BC is :
View SolutionIn a triangle ABC the expression `a cosB cosC+b cosA cosB` equals to :
View SolutionIn a acute triangle ABC, altitudes from the vertices A, B and C meet the opposite sides at the points D, E and F respectively. If the radisu of the circumcircle of `Delta AFE,DeltaBFD, DeltaCED, DeltaABC` be respectively `R_(1), R_(2),R_(3) and R`. Then the maximum value of `R_(1)+R_(2)+R_(3)` is :
View SolutionA circle of area 20 sq. units is entered at the point O. Suppose `DeltaABC` is inscribed in that circle and has area 8 sq. units. The central angles `alpha, beta and gamma` are as shown in the figure. The value of `(sin alpha+sin beta+sin gamma)` is equal to :
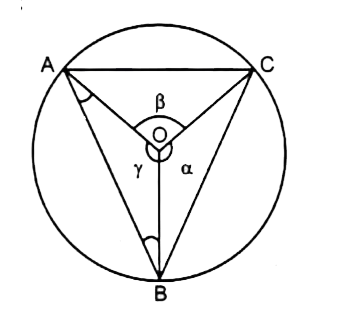
View Solution
Exercise-1 : Single Choice Problems questions and complete solutions for chapter SOLUTION OF TRIANGLES of VK JAISWAL MATHS (HINGLISH) of Class 12