Complete Solutions to Exercise-5 : Subjective Type Problems of chapter SOLUTION OF TRIANGLES of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | SOLUTION OF TRIANGLES |
| VK JAISWAL | Exercise-5 : Subjective Type Problems |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
If the median AD of triangle ABC makes an angle `pi/4` with the side BC, then find the value of `|cotB-cotC|dot`
View SolutionIn a `DeltaABC,a= sqrt(3), b=3 and angleC=(pi)/(3)`. Let internal angle bisectors of angle C intersects side AB at D and altitude from B meets the angle bisector CD at E. If `Q_(1) and Q_(2)` are incentres of `DeltaBEC and DeltaBED`. Find the distance between the vertex B and orthocentre of `DeltaO_(1)EO_(2)`.
View SolutionIn a `Delta ABC`; inscribed circle with centre `I` touches sides `AB, AC and BC at D, E, F` respectively.Let area of quadrilateral ADIE is 5 units and area of quadrilteral BFID is 10 units. Find the value of `cos(C/2)/sin((A-B)/2)`.
View SolutionIf `Delta` be area of incircle of a triangle ABC and `Delta_1,Delta_2,Delta_3` be the area of excircles then find the least value of `(Delta_1 Delta_2 Delta_3)/(729 Delta^3)`
View SolutionIn `DeltaABC, b=c, angleA=106^(@)`, M is an interior point such that `angleMBA=7^(@), angleMAB=23^(@) and angle MCA=theta^(@), " then "(theta)/(2)` is equal to
(where notations have their usual meaning)
View SolutionIn an acute angled triangle ABC, `angleA=20^(@)`, let DEF be the feet of altitudes through A, B, C respectively and H is the orthocentre of `DeltaABC`. Find `(AH)/(AD)+(BH)/(BE)+(CH)/(CF)`.
View SolutionLet `DeltaABC` be inscribed in a circle having radius unity. The three internal bisectors of the angles A, B and C are extended to intersect the circumcircle of `DeltaABC` at `A_(1)B_(1) and C_(1)` respectively. Then `(A A_(1)"cos"(A)/(2)BB_(1)"cos"(B)/(2)+C C_(1)"cos"(C)/(2))/(sinA+sinB+sinC)=`
View SolutionIf the quadratic equation `ax^2+bx+c=0` has equal roots where a, b, c denotes the lengths of the sides opposite to vertex A, B and C of the `DeltaABC` respectively then find the number of integers in the range of `sinA/sinC+sinC/sinA`
View Solutionif ABC is a triangle and `tan(A/2), tan(B/2), tan(C/2)` are in H.P. Then find the minimum value of `cot(B/2)`
View SolutionIn `DeltaABC`, if circumradius 'R' and inradius 'r' are connected by relation `R^(2)-4Rr+8r^(2)-12r+9=0`, then the greatest integer which is less than the semiperimeter of `DeltaABC` is :
View SolutionSides AB and AC in an equilateral triangle ABC with side length 3 is extended to form two rays from point A as shown in the figure. Point P is chosen outside the triangle ABC and between the two rays such that `angleABP+angleBCP=180^(@)`. If the maximum length of CP is M, then `M^(2)//2` is equal to :
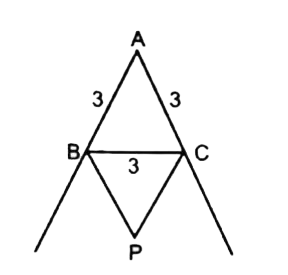
View SolutionLet a, b, c be sides of a triangle ABC and `Delta` denotes its area .
If `a=2, Delta=sqrt(3) and a cosC+sqrt(3) a sinC-b-c=0`, then find the value of `(b+c)`.
(symbols used have usual meaning in `DeltaABC`).
View SolutionCircumradius of `DeltaABC` is 3 cm and its area is `6 cm^(2)`. If DEF is the triangle formed by feet of the perpendicular drawn from A,B and C on the sides BC, CA and AB, respectively, then the perimeter of `DeltaDEF` (in cm) is _____
View Solution
Exercise-5 : Subjective Type Problems questions and complete solutions for chapter SOLUTION OF TRIANGLES of VK JAISWAL MATHS (HINGLISH) of Class 12