Complete Solutions to Solved Examples of chapter CONGRUENCE OF TRIANGLES of Class 7 book with complete answers and questions
| Class 7 | MATHS |
| Chapter | CONGRUENCE OF TRIANGLES |
| MTG IIT JEE FOUNDATION | Solved Examples |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
In the given figure, we have PQ = SR and Pr = SQ. Prove that:
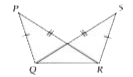
`DeltaPQR~=DeltaSRQ`
View SolutionIn the given figure, we have PQ = SR and Pr = SQ. Prove that:

`anglePQR=angleSRQ`
View SolutionIn the given figure, we have C is the mid-point of AB and DA = DB.
Prove that : `angleDCA=angleDCB`.
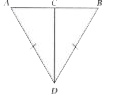
View SolutionThe diagonals of a parallelogram bisect each other.
View SolutionIn the adjoining figure, `DeltaABC` is an isosceles triangle in which AB = AC and AD is the bisector of `angleA`. Prove that:
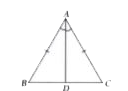
`DeltaADB~=DeltaADC`
View SolutionIn the adjoining figure, `DeltaABC` is an isosceles triangle in which AB = AC and AD is the bisector of `angleA`. Prove that:
`angleB=angleC`
View SolutionIn the adjoining figure, `DeltaABC` is an isosceles triangle in which AB = AC and AD is the bisector of `angleA`. Prove that:

BD = CD
View SolutionIn the adjoining figure, `DeltaABC` is an isosceles triangle in which AB = AC and AD is the bisector of `angleA`. Prove that:
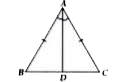
`ADbotBC`
View SolutionIn the adjoining figure, `DeltaABC` is an isosceles triangle in which AB = AC. If `BMbotACandCNbotAB`, prove that: `DeltaBMC~=DeltaCNB`
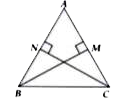
View SolutionIn the adjoining figure, `DeltaABC` is an isosceles triangle in which AB = AC. If `BMbotACandCNbotAB`, prove that:
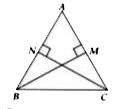
BM = CN
View SolutionIn the given figure, KK' and LL' are equal and perpendicular to AC. Show that `DeltaKK'MandDeltaLL'M` are congruent.
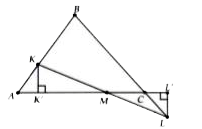
View SolutionIn the figure, it is given that LM = NM, `MLbotPQandMNbotPR`. Prove that `angleLPM=angleNPM`.
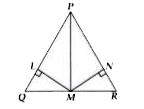
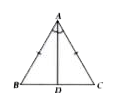
View SolutionIn the adjoining figure, `DeltaABC` is an isosceles triangle in which AB = AC and AD is a median.
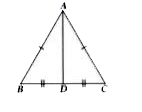 Prove that:
Prove that:
`DeltaADB~=DeltaADC`
View SolutionIn the adjoining figure, `DeltaABC` is an isosceles triangle in which AB = AC and AD is a median.
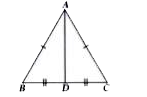 Prove that:
Prove that:
`angleBAD=angleCAD`
View SolutionShow that the diagonals of a rhombus bisect each other at right angles.
View SolutionIf the opposite sides of a quadrilateral are equal, prove that the quadrilateral is a parallelogram.
View SolutionIn both the given figures, AB = AC and DB = DC. Prove that `angleABD=angleACD`.
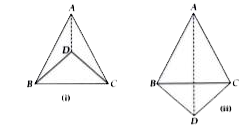
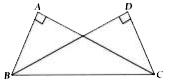
View SolutionIn the given figure, triangles ABC and DCB are right angled at A and D respectively and AC = DB, then prove that `angleACB` = `angleDBC`.
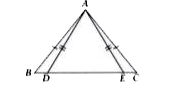
View SolutionIn the given figure, AB = AC and AD = AE. Prove that:
`DeltaABD~=DeltaACE`
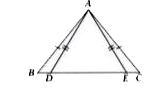
View SolutionIn the given figure, AB = AC and AD = AE. Prove that:
BD = CE
View Solution`A B` is a line segment. `A X\ a n d\ B Y` are two equal line segments drawn on opposite sides of line `A B` such that `A X||B Ydot` If `A B\ a n d\ X Y` intersect each other at `P ,` prove that ` A P X~=B P Y` (ii) `A B\ a n d\ X Y` bisect each other.
View SolutionShow that the given triangles are congruent.

View SolutionIf the diagonals of a quadrilateral bisect each other; then the quadrilateral is a parallelogram.
View SolutionIn the given figure, if S is the angle bisector of `angleQPR` then, show that `DeltaPQS~=DeltaPRS`.
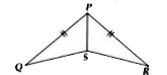
View Solution
Solved Examples questions and complete solutions for chapter CONGRUENCE OF TRIANGLES of MTG IIT JEE FOUNDATION of Class 7
All Exercises from MTG IIT JEE FOUNDATION Class 7 MATHS CONGRUENCE OF TRIANGLES
- Assertion & Reaction Type
- Comprehension Type
- Exercise (Multiple Choice Questions) (LEVEL - 1)
- ILLUSTRATIONS
- Match the following
- NCERT Section (Exercise 7.1)
- NCERT Section (Exercise 7.2)
- Olympiad/HOTS Corner
- Solved Examples
- Subjective Problems (Long Answer Type)
- Subjective Problems (Short Answer Type)
- Subjective Problems (Very Short Answer Type)