Complete Solutions to Subjective Problems (Short Answer Type) of chapter CONGRUENCE OF TRIANGLES of Class 7 book with complete answers and questions
| Class 7 | MATHS |
| Chapter | CONGRUENCE OF TRIANGLES |
| MTG IIT JEE FOUNDATION | Subjective Problems (Short Answer Type) |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
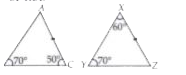
State whether the following triangles are congruent or not.
View SolutionStudy the given and prove that `DeltaPQR` is an isosceles triangle.

View SolutionIn Figure, it is given that `L M=M N ,\ Q M=M R ,\ M L\ _|_P Q\ a n d\ M N\ _|_P Rdot\ ` Prove that `P Q=P R`
View SolutionIn the given figure, AB = AD and `angle1=angle2`. Prove that : `DeltaABC~=DeltaADC`

View SolutionIn the given figure, AB = AD and `angle1=angle2`. Prove that : BC = DC
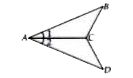
View SolutionIn the given figure, Ab = CD and `angleABC=angleDCB=90^(@)`. Prove that AC = DB.
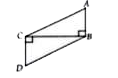
View SolutionProve that `DeltaABD~=DeltaCDB`.
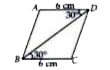
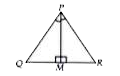
View SolutionPQR is a triangle in which PM is the bisector of `anglePandPMbotQR`. Prove that:
`DeltaPMQ~=DeltaPMR`
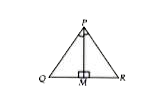
View SolutionPQR is a triangle in which PM is the bisector of `anglePandPMbotQR`. Prove that:
QM = RM
View SolutionIn the figure `bar(AB)||bar(XY)`. BX and AY are the transversals intersecting at O, such that `bar(OA)=bar(OY)`. Show that `DeltaOAB~=DeltaOYX`.

View SolutionIn the given figure, `angleBAC=angleCDBandangleACB=angleDBC`. Prove that AC = DB.

View SolutionIn `DeltaABC`, BD and CE are perpendicluars to the sides AC and AB respectively and BD = CE. Prove that `DeltaBCD~=DeltaCBE`.
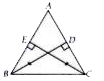
View Solution
Subjective Problems (Short Answer Type) questions and complete solutions for chapter CONGRUENCE OF TRIANGLES of MTG IIT JEE FOUNDATION of Class 7
All Exercises from MTG IIT JEE FOUNDATION Class 7 MATHS CONGRUENCE OF TRIANGLES
- Assertion & Reaction Type
- Comprehension Type
- Exercise (Multiple Choice Questions) (LEVEL - 1)
- ILLUSTRATIONS
- Match the following
- NCERT Section (Exercise 7.1)
- NCERT Section (Exercise 7.2)
- Olympiad/HOTS Corner
- Solved Examples
- Subjective Problems (Long Answer Type)
- Subjective Problems (Short Answer Type)
- Subjective Problems (Very Short Answer Type)