Complete Solutions to EXERCISE TRUE OR FALSE of chapter TRIANGLES of Class 7 book with complete answers and questions
| Class 7 | MATHS |
| Chapter | TRIANGLES |
| NCERT EXEMPLAR | EXERCISE TRUE OR FALSE |
| Number Of Questions | 69 |
| Academic Year | 2023-24 |
The difference between the lengths of any two sides of a triangle is smaller than the length of third side.
View SolutionSum of any two angles of a triangle is always greater than the third angle.
View SolutionThe sum of the measures of three angles of a triangle is greater than` 180^@`
View SolutionIt is possible to have a right-angled equilateral triangle
View SolutionState True or False
If M is the mid-point of a line segment AB, then we can say that AM and MB are congruent
View SolutionIt is possible to have a triangle in which two of the angles are right angles
View SolutionIt is possible to have a triangle in which two of the angles are obtuse.
View SolutionIt is possible to have a triangle in which two angles are acute.
View SolutionState Whether Statements are True or False : It is possible to have a triangle in which each angle is less than `60°`.
View SolutionState Whether Statement is True or False : It is possible to have a triangle in which each angle is greater than `60°`.
View SolutionIt is possible to have a triangle in which each angle is equal to `60°.`
View SolutionA right-angled triangle may have all sides equal.
View SolutionA one rupee coin is congruent to a five rupee coin. (True/False)
View SolutionTwo acute angles are congruent
View SolutionTwo right angles are congruent
View SolutionTwo figures are congruent, if they have the same shape.
View SolutionIf the areas of two squares is same, they are congruent.
View SolutionIf the areas of two rectangles are same, they are congruent
View SolutionIf the areas of two circles are the same, they are congruent.
View SolutionTwo squares having same perimeter are congruent.
View SolutionTwo circles having same circumference are congruent.
View SolutionState True or False : If three angles of two triangles are equal, triangles are congruent.
View SolutionIf hypotenuse and an acute angle of one right triangle are equal to the hypotenuse and an acute angle of another right triangle, then the triangles are congruent
View SolutionThe measure of three angles of a triangle are in the ratio `5 : 3 : 1`. Find the measures of these angles.
View SolutionIn Fig. 6.31(i) and (ii), find the values of a, b and c.
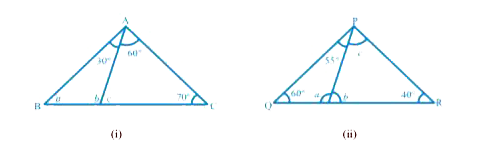
View SolutionIn triangle XYZ, the measure of angle X is `30°` greater than the measure of angle Y and angle Z is a right angle. Find the measure of` ∠Y.`
View SolutionIn a triangle ABC, the measure of angle A is ` 40°` less than the measure of angle B and `50°` less than that of angle C. Find the measure of `∠ A.`
View SolutionI have three sides. One of my angle measures `15°`. Another has a measure of` 60°`. What kind of a polygon am I? If I am a triangle, then what kind of triangle am I?
View SolutionJiya walks 6 km due east and then 8 km due north. How far is she from her starting place?
View SolutionJayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures 60 metres `times` 80 metres. How much shorter is the route across the park than the route around its edges?
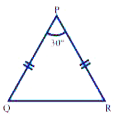
View SolutionIn `∆PQR` of Fig. 6.32, PQ = PR. Find the measures of `∠Q and ∠R.`
View SolutionIn Fig. 6.33, find the measures of `∠ x and ∠ y.`

View SolutionIn Fig. 6.34, find the measures of `∠ PON and ∠ NPO`

View SolutionFind the measure of `∠ A` in Fig. 6.36
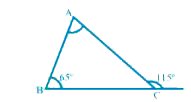
View SolutionIn a right-angled triangle if an angle measures `35°`, then find the measure of the third angle.
View SolutionEach of the two equal angles of an isosceles triangle is four times the third angle. Find the angles of the triangle
View SolutionThe angles of a triangle are in the ratio` 2 : 3 : 5`. Find the angles
View SolutionIf the sides of a triangle are produced in an order, show that the sum of the exterior angles so formed is `360°. `
View SolutionIn `∆ABC`, if `∠A = ∠C`, and exterior angle `ABX = 140°`, then find the angles of the triangle
View SolutionFind the values of x and y in Fig. 6.37
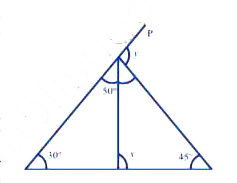
View SolutionFind the value of x in Fig. 6.38
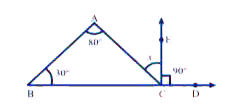
View SolutionThe angles of a triangle are arranged in descending order of their magnitudes. If the difference between two consecutive angles is `10°`, find the three angles.
View SolutionIn `∆ ABC, DE || BC` (Fig. 6.39). Find the values of x, y and z.
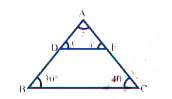
View SolutionIn Fig. 6.40, find the values of x, y and z.

View SolutionIf one angle of a triangle is `60°` and the other two angles are in the ratio `1 : 2`, find the angles.
View SolutionIn `∆PQR`, if 3`∠P = 4∠Q = 6∠R`, calculate the angles of the triangle.
View SolutionIn `∆DEF, ∠D = 60°, ∠E = 70°` and the bisectors of` ∠E and ∠F` meet at O. Find (i) `∠F` (ii)` ∠EOF`.
View SolutionIn Fig. 6.41, `∆PQR` is right-angled at P. U and T are the points on line QRF. If ` QP || ST` and `US || RP`, find` ∠S`
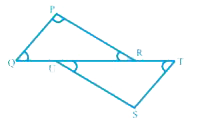
View SolutionIn Fig. 6.44, if RP = RQ, find the value of x.
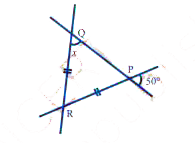
View SolutionIn Fig. 6.45, if ST = SU, then find the values of x and y.
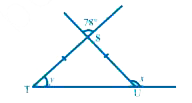
View SolutionCheck whether the following measures (in cm) can be the sides of a right-angled triangle or not.
1.5, 3.6, 3.9
View SolutionHeight of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.
View SolutionIn Fig. 6.46, if y is five times x, find the value of z.
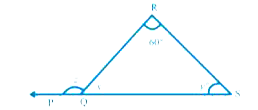
View SolutionThe lengths of two sides of an isosceles triangle are 9 cm and 20 cm. What is the perimeter of the triangle? Give reason.
View SolutionWithout drawing the triangles write all six pairs of equal measures in each of the following pairs of congruent triangles.
(i) `Delta STU approx Delta DEF`
(ii) `Delta ABC approx Delta LMN`
(iii) `Delta YZX approx PQR`
(iv) `Delta XYZ approx Delta MLN`
View SolutionABC is an isosceles triangle with AB = AC and D is the mid-point of base BC.
(a) State three pairs of equal parts in the triangles ABD and ACD.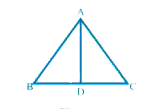
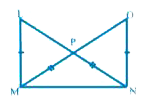
View SolutionIn Figure, it is given that LM = ON and NL = MO
(a) State the three pairs of equal parts in the triangles NOM and MLN.
(b) Is `∆NOM ≅ ∆MLN`. Give reason
View SolutionTriangles DEF and LMN are both isosceles with DE = DF and LM = LN, respectively. If DE = LM and EF = MN, then, are the two triangles congruent? Which condition do you use? If `∠ E = 40°`, what is the measure of `∠ N`?
View SolutionIf` ∆PQR and ∆SQR` are both isosceles triangle on a common base QR such that P and S lie on the same side of QR. Are triangles PSQ and PSR congruent? Which condition do you use?
View SolutionState which of the following pairs of triangles are congruent. If yes, write them in symbolic form (you may draw a rough figure).
`∆ PQR : PQ = 3.5 cm, QR = 4.0 cm, ∠ Q = 60° `
`∆ STU : ST = 3.5 cm, TU = 4 cm, ∠ T = 60°`
View SolutionState which of the following pairs of triangles are congruent. If yes, write them in symbolic form (you may draw a rough figure).
`∆ABC : AB = 4.8 cm, ∠ A = 90°, AC = 6.8 cm `
`∆XYZ : YZ = 6.8 cm, ∠ X = 90° , ZX = 4.8 cm`
View SolutionIn Figure, PQ = PS and `∠ 1 = ∠ 2`.
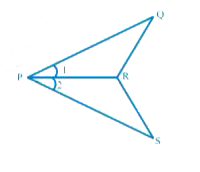
(i) Is `∆PQR ≅ ∆PSR`? Give reasons.
(ii) Is QR = SR? Give reasons.
View SolutionIn Figure, `∠1 = ∠ 2 and ∠ 3 = ∠ 4`
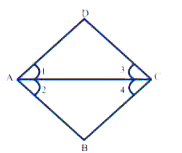
. (i) Is` ∆ADC ≅ ∆ ABC`? Why ?
(ii) Show that AD = AB and CD = CB.
View SolutionObserve Figure and state the three pairs of equal parts in triangles ABC and DBC.
(i) Is` ∆ABC ≅ ∆DCB`? Why? (ii) Is AB = DC? Why? (iii) Is AC = DB? Why
View SolutionIn Fig. 6.55,` QS ⊥ PR, RT ⊥ PQ` and QS = RT.
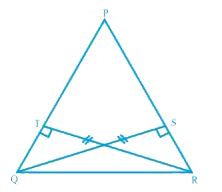 (i) Is` ∆ QSR ≅ ∆ RTQ`? Give reasons. (ii) Is `∠ PQR = ∠ PRQ`? Give reasons.
(i) Is` ∆ QSR ≅ ∆ RTQ`? Give reasons. (ii) Is `∠ PQR = ∠ PRQ`? Give reasons.
View SolutionPoints A and B are on the opposite edges of a pond as shown in Fig. 6.56. To find the distance between the two points, the surveyor makes a right-angled triangle as shown. Find the distance AB.

View SolutionTwo poles of 10 m and 15 m stand upright on a plane ground. If the distance between the tops is 13 m, find the distance between their feet.
View SolutionThe foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground, Find the length of the ladder.
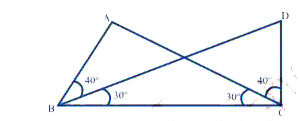
View SolutionIn Figure, state the three pairs of equal parts in `∆ABC and ∆EOD`. Is` ∆ABC ≅ ∆ EOD`? Why?

View Solution
EXERCISE TRUE OR FALSE questions and complete solutions for chapter TRIANGLES of NCERT EXEMPLAR of Class 7