State True or False
If M is the mid-point of a line segment AB, then we can say that AM and MB are congruent
To determine whether the statement "If M is the mid-point of a line segment AB, then we can say that AM and MB are congruent" is true or false, we can follow these steps:
1. Understanding the Definition of Midpoint:
- A midpoint of a line segment is a point that divides the segment into two equal parts.
2. Identifying Points:
- Let’s denote the line segment as AB, where A and B are the endpoints.
- Let M be the midpoint of line segment AB.
3. Applying the Definition:
- Since M is the midpoint, by definition, the lengths of the segments AM and MB must be equal. This means that:
AM=MB
4. Understanding Congruence:
- In geometry, two segments are said to be congruent if they have the same length. Since AM and MB are equal in length, we can say:
AM≅MB
5. Conclusion:
- Therefore, we can conclude that the statement is true: if M is the midpoint of line segment AB, then AM and MB are indeed congruent.
Final Answer:
- The statement is True.
- A midpoint of a line segment is a point that divides the segment into two equal parts.
- Let’s denote the line segment as AB, where A and B are the endpoints.
- Let M be the midpoint of line segment AB.
- Since M is the midpoint, by definition, the lengths of the segments AM and MB must be equal. This means that:
AM=MB
- In geometry, two segments are said to be congruent if they have the same length. Since AM and MB are equal in length, we can say:
AM≅MB
- Therefore, we can conclude that the statement is true: if M is the midpoint of line segment AB, then AM and MB are indeed congruent.
- The statement is True.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the figure P(3, 2) is the mid-point of the line segment AB. What are the co-ordinates of A and B respectively:
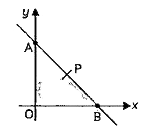 A(4,0) and (6, 0)B(0,4) and (6,0)C(0,4) and (0,6)D(0,-4) and (-6, 0)
A(4,0) and (6, 0)B(0,4) and (6,0)C(0,4) and (0,6)D(0,-4) and (-6, 0)In the given figure, M is the mid point of line segment AB whose length is 2a. Semicircles having diameters AM, MB and AB are drawn at the same side of the line. The radius of a circle toughing all the three semicircle is
 A2a3Ba2Ca3Da4
A2a3Ba2Ca3Da4The mid-point of the line segment joining the points (- 2, 4) and (6, 10) is
A(2, 5)B(2, 7)C(3, 7)D(3, 8)
What is mid - point of line segment AB, where A (-5,0) and B(0,5) ?
View SolutionState True or False:
A ratio can be equal to 1.
View SolutionIn give figur l||m and M is the mid-point of a line segment AB .Show that M is also the mid- point of any line segment CD,having its end points on l and m,respectively.
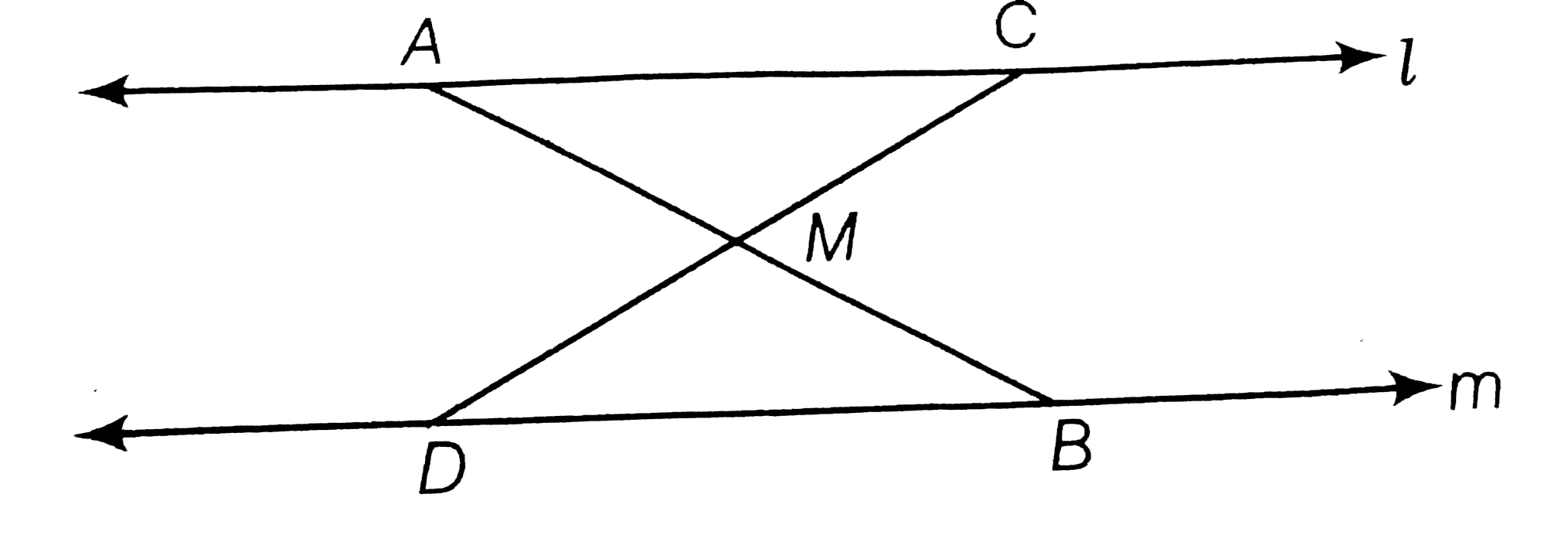
View SolutionIn the given figure, P (4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
View SolutionThe mid point of the line segment joining the points (−5,7)and(−1,3) is
View Solution
