Complete Solutions to प्रश्नावली 12.1 (लघु उत्तरीय प्रश्न) of chapter वृत्त of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | वृत्त |
| ALOK BHARTI PUBLICATION | प्रश्नावली 12.1 (लघु उत्तरीय प्रश्न) |
| Number Of Questions | 9 |
| Academic Year | 2023-24 |
(a) किसी वृत्त की त्रिज्या 10 सेमी एवं इसकी एक जीवा की लम्बाई 16 सेमी है। केन्द्र से जीवा की दूरी ज्ञात करें।
(b) किसी वृत्त की उस जीवा की लम्बाई ज्ञात करें जिसकी केन्द्र से दूरी 3 सेमी तथा वृत्त का व्यास 10 सेमी है।
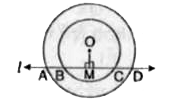
View Solutionदो संकेन्द्रिय वृत्तों, जिनका केन्द्र O है, को एक सरल रेखा क्रमशः बिंदुओं A, B, C एवं D पर काटती है। यदि `AD=12` सेमी एवं `BC=8` सेमी हो तो AB एवं CD की लम्बाई ज्ञात करें।
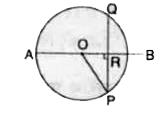
View Solutionबगल की आकृति में वृत्त C(O, r) का व्यास AB जीवा PQ को R बिन्दु पर समद्विभाग करता है। यदि `PR=QR=8` सेमी हो तथा `RB=4` सेमी हो तो वृत्त की त्रिज्या ज्ञात करें।
View Solution(a) 5 सेमी एवं 3 सेमी त्रिज्या वाले दो वृत्त दो भिन्न-बिंदुओं पर प्रतिच्छेद करते है तथा उनके केन्द्रो के बीच की दूरी 4 सेमी है। उभयनिष्ठ जीवा की लम्बाई ज्ञात करें।
(b) दो वृत्त जिनकी त्रिज्याएँ क्रमशः 10 सेमी एवं 17 सेमी है, एक-दूसरे को दो भिन्न बिंदुओं पर प्रतिच्छेद करते है। यदि उनकी उभयनिष्ठ जीवा की लम्बाई 16 सेमी हो तो उनके केन्द्रो के बीच की दूरी ज्ञात करें।
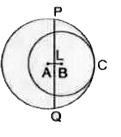
View Solutionदो वृत्त जिनके केन्द्र बिन्दु क्रमशः A तथा B है तथा त्रिज्याएँ क्रमशः 5 सेमी एवं 3 सेमी है, एक-दूसरे को बिन्दु C पर आन्तरिकतः स्पर्श करते है। यदि AB का लम्ब समद्विभाजक वृत्त को P एवं Q बिंदुओं पर प्रतिच्छेद करता है तो PQ की लम्बाई ज्ञात करें।
View Solutionकिसी वृत्त की दो जीवाएँ AB एवं AC समान है। साबित करें कि `angleBAC` का समद्विभाजक वृत्त के केन्द्र से होकर गुजरेगा।
View Solutionसिद्ध करें कि किसी वृत्त का व्यास उसकी सबसे बड़ी जीवा होती है।
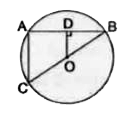
View Solutionदी गई आकृति में O वृत्त का केन्द्र है तथा `OD_|_AB` है। सिद्ध करें कि। `CA=2OD`
View Solutionकिसी दिये गए वृत्त का केन्द्र अज्ञात हो तो इसे ज्ञात करने की विधि ज्ञात करें।
View Solution
प्रश्नावली 12.1 (लघु उत्तरीय प्रश्न) questions and complete solutions for chapter वृत्त of ALOK BHARATI MATHS (HINDI) of Class 9
All Exercises from ALOK BHARTI PUBLICATION Class 9 MATHS वृत्त
- प्रश्नावली 12.1 (अतिलघु उत्तरीय प्रश्न)
- प्रश्नावली 12.1 (अतिलघु उत्तरीय प्रश्न) रिक्त स्थान
- प्रश्नावली 12.1 (दीर्घ उत्तरीय प्रश्न)
- प्रश्नावली 12.1 (बहुविकल्पीय प्रश्न)
- प्रश्नावली 12.1 (लघु उत्तरीय प्रश्न)
- प्रश्नावली 12.2 (अतिलघु उत्तरीय प्रश्न)
- प्रश्नावली 12.2 (अतिलघु उत्तरीय प्रश्न) रिक्त स्थान
- प्रश्नावली 12.2 (बहुविकल्पीय प्रश्न)
- प्रश्नावली 12.2 (लघु उत्तरीय प्रश्न)
- प्रश्नावली 12.3 (अतिलघु उत्तरीय प्रश्न)
- प्रश्नावली 12.3 (अतिलघु उत्तरीय प्रश्न) रिक्त स्थान
- प्रश्नावली 12.3 (दीर्घ उत्तरीय प्रश्न)
- प्रश्नावली 12.3 (बहुविकल्पीय प्रश्न)
- प्रश्नावली 12.3 (लघु उत्तरीय प्रश्न)
- साधित उदाहरण