Complete Solutions to साधित उदाहरण of chapter वृत्त of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | वृत्त |
| ALOK BHARTI PUBLICATION | साधित उदाहरण |
| Number Of Questions | 51 |
| Academic Year | 2023-24 |
एक वृत्त की त्रिज्या 17 सेमी है तथा इसकी एक जीवा की लम्बाई 30 सेमी है। इस जीवा की केन्द्र से दुरी ज्ञात करे।
View SolutionPQ एवं RS एक वृत्त जिसका केन्द्र O है, की दो समांतर जीवाएँ है। `PQ=16` सेमी तथा `RS=12` सेमी है। यदि वृत्त की त्रिज्या 10 सेमी हो तो दोनों जीवाओं के बीच की दूरी प्राप्त करे यदि (i) PQ एवं RS वृत्त के केन्द्र O के एक ही ओर स्थित हो। (ii) PQ एवं RS वृत्त के केन्द्र O के विपरीत हो।
View Solutionयदि कोई सरल रेखा l दो संकेन्द्रीत वृत्तों को A, B, C तथा D बिंदुओं को परिच्छेद करती है, तो सिद्ध करे कि AB = CD.
View Solutionदी गई आकृति में `overset(frown)(AB)~=overset(frown)(CD)` सिद्ध करे कि
`angleA=angleB`
View Solutionसिद्ध करे कि किसी वृत्त में दो समांतर जीवाओं के मध्य बिंदुओं को मिलाने वाली रेखा वृत्त के केन्द्र से गुजरती है।
View Solutionदो वृत्त जिनके केन्द्र क्रमशः O एवं O' है, एक-दूसरे को P बिंदु पर काटते है। P बिंदु से होते हुए OO' के समांतर एक रेखा l खींची गई है जो दोनों वृत्तों को क्रमशः C एवं D बिंदुओं पर काटती है। सिद्ध करे कि `CD=2OO'`
View Solutionयदि किसी वृत्त का व्यास उसकी दो जीवाओं में से प्रत्येक को समद्विभाग करता है तो सिद्ध करे कि वे दोनों जीवाएँ समांतर होगी।
View Solutionदिए गए वृत्त `C(O,r)` में दो समान जीवाएँ AB एवं CD एक-दूसरे को P बिंदु पर लम्बवत काटती है। यदि L और M क्रमशः AB एवं CD के मध्य बिंदु हो तो सिद्ध करे कि OLPM एक वर्ग होगा।
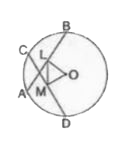
View Solutionदी गई आकृति में, दो समान जीवाओं AB तथा CD के मध्य बिंदु L क्रमशः M एवं है। यदि वृत्त का केन्द्र O हो तो साबित करे कि
(i) `angleOLM=angleOML`
(ii) `angleALM=angleCML`
(iii) `angleBLM=angleDML`
View Solutionदो वृत्त जिनकी त्रिज्याएँ क्रमशः 10 सेमी एवं 8 सेमी है, एक-दूसरे को P एवं Q बिंदुओं पर काटती है एवं उनकी उभयनिष्ठ जीवा की लम्बाई 12 सेमी है। दोनों वृत्तों के केन्द्रो के बीच की दूरी ज्ञात करे।
View Solutionएक वृत्त C(O, r) में r = 5 सेमी तथा इसकी दो जीवाएँ AB एवं AC इस प्रकार है कि `AB=AC=6` सेमी है। वृत्त की जीवा BC की लम्बाई ज्ञात करे।
View Solutionएक वृत्त जिसका केन्द्र O है, की दो जीवाएँ AB एवं BC इस प्रकार है कि `angleABO=angleCBO`। सिद्ध करे कि AB = BC
View Solutionसिद्ध करे कि किसी वृत्त की एक जीवा का लम्ब समद्विभाजक उसके संगत चाप को भी समद्विभाजित करता है।
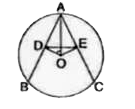
View Solutionदी गई आकृति में, AB तथा AC एक वृत्त जिसका केन्द्र O है, की दो समान जीवाएँ है। यदि `OD_|_AB` एवं `OE_|_AC` हो तो सिद्ध करे कि ADE एक समद्विबाहु त्रिभुज होगा।
View SolutionAB तथा AC एक वृत्त जिसका केन्द्र O तथा त्रिज्या r है, की दो जीवाएँ है। यदि `AB=2AC` तथा केन्द्र O से इन जिवाओं पर डाले गए शीर्षलम्बो की लम्बाई क्रमशः 'a' तथा 'b' हो तो सिद्ध करे कि `4b^(2)=a^(2)+3r^(2)`
View Solution20 मीटर त्रिज्या का एक वृत्ताकार पार्क एक कॉलोनी में स्थित है। तीन लड़के अंकुर, सैय्यद तथा डेविड इसकी परिसीमा पर बराबर दूरी पर बैठे है और प्रत्येक के पास एक खिलौना टेलीफोन आपस में बात करने के लिए है। प्रत्येक फोन की डोरी की लम्बाई ज्ञात कीजिए।
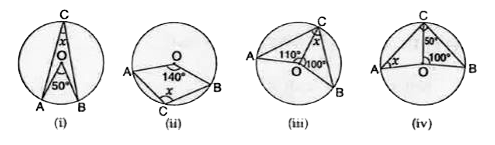
View Solutionयदि नीचे दी गई आकृतियों में वृत्त का केन्द्र O हो तो प्रत्येक चित्र में x का मान ज्ञात करे।
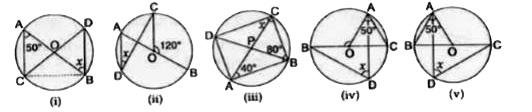
View Solutionनीचे दी गई आकृतियों में वृत्त का केन्द्र O है। प्रत्येक दशा में x का मान ज्ञात करे।
View Solutionकिसी वृत्त की एक जीवा वृत्त की त्रिज्या के बराबर है। जीवा द्वारा लघु चाप के किसी बिन्दु पर अंतरित कोण तथा दीर्घचाप के किसी बिन्दु पर भी अंतरित कोण ज्ञात कीजिए।
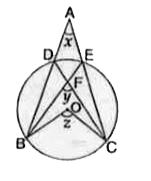
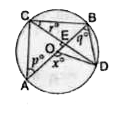
View Solutionदी गई आकृति में बिन्दु वृत्त का केन्द्र है। सिद्ध करे कि
`anglex+angley=anglez`
View Solutionदी गई आकृति में वृत्त का केन्द्र O है। इसकी दो जीवाएँ AB तथा CD, एक-दूसरे को वृत्त के अभ्यंतर में E बिन्दु पर प्रतिच्छेद करती है। सिद्ध करे कि
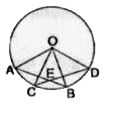
`angleAOC+angleBOD=2angleAEC`
View Solutionएक वृत्त जिसका केन्द्र O है, के लघुचाप `overset(frown)(AB)` पर एक बिन्दु C है। यदि `angleACB=x^(@)` एवं `angleAOB=y^(@)` हो तो y को x के रूप में व्यक्त करे। फिर यदि ACBO एक समांतर चतुर्भुज हो तो x का मान ज्ञात करे।
View Solutionसिद्ध करे कि किसी समपंचभुज के कोई चार शीर्ष बिन्दु चक्रीय होते है।
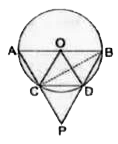
View Solutionदी गई आकृति में AOB वृत्त C(O,r) का व्यास है तथा जीवा CD = त्रिज्या OC है। जब AC एवं BD को बढ़ाया जाता है, तो वे एक-दूसरे से P बिन्दु पर मिलते है। सिद्ध करे कि
`angleAPB=60^(@)`
View Solutionकिसी वृत्त के दो व्यास एक-दूसरे को समकोण पर प्रतिच्छेद करते है। सिद्ध करे कि इन दोनों व्यासो के नियत बिंदुओं को मिलाने से एक वर्ग बनता है।
View Solutionकिसी वृत्त C(O, r) का व्यास AB, उसी वृत्त की एक जीवा PQ को समद्विभाग करता है तथा `AQ||PB` हो तो सिद्ध करे कि PQ भी वृत्त का व्यास होगा।
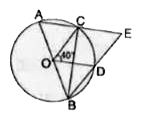
View Solutionदी गई आकृति में AB वृत्त का व्यास है तथा O इसका केन्द्र है। इसकी दो जीवाएँ AC एवं BD एक-दूसरे से E बिन्दु पर मिलती है एवं `angleCOD=40^(@)` है तो `angleCED` का मान ज्ञात करे।
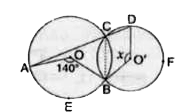
View Solutionदी गई आकृति में O एवं O' उन दो वृत्तों के केन्द्र है जो एक-दूसरे को B एवं C बिन्दु पर प्रतिच्छेद करते है तथा ACD एक सरल रेखा है। यदि `angleAOB=140^(@)` हो तो 'x' का मान ज्ञात करे।
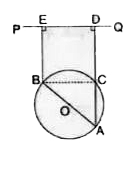
View Solutionदी गई आकृति में AB वृत्त का व्यास तथा इसका केन्द्र बिन्दु O है। `BE_|_PQ` एवं `AD_|_PQ` है। सिद्ध करे कि
`BE=CD`
View Solutionदी गई आकृति में AB वृत्त का व्यास तथा O इसका केन्द्र है। फिर `CD_|_AB` जो AB को E बिन्दु पर काटता है। p, q एवं r का मान x के पदों में ज्ञात करे।
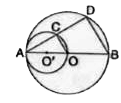
View Solutionदी गई आकृति में AB उस वृत्त का व्यास है, जिसका केन्द्र O है तथा AO को व्यास मानकर एक दूसरा वृत्त खींचा गया है। वृत्त C(O, r) की जीवा AD, वृत्त C(O', r') को C बिन्दु पर परिच्छेद करती है। सिद्ध करे कि BD = 2OC.
View Solutionकिसी चक्रीय चतुर्भुज का एक कोण अपने सम्मुख कोण का `(2)/(3)` गुना है। इन कोणो का मान ज्ञात करे।
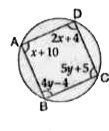
View Solutionदी गई आकृति में x तथा y का मान ज्ञात करे।
`angleA=(x+10),angleB=(4y-4)`,
`angleC=(5y+5),angleD=(2x+4)`
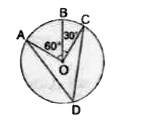
View Solutionदी गई आकृति में केन्द्र बिन्दु O वाले एक वृत्त पर तीन बिन्दु A, B और C इस प्रकार है कि `angleBOC=30^(@)` तथा `angleAOB=60^(@)` है। यदि चाप ABC के अतिरिक्त वृत्त पर एक बिन्दु है तो `angleADC` का मान ज्ञात करे।
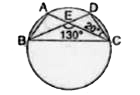
View Solutionबगल की आकृति में दिए गए वृत्त पर A, B, C एवं D चार बिन्दु है। AC और BD एक बिन्दु E पर इस प्रकार प्रतिच्छेद करते है कि `angleBEC=130^(@)` तथा `angleECD=20^(@)` है। `angleBAC` का मान ज्ञात करें।
View SolutionABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण एक-दूसरे को बिन्दु E पर प्रतिच्छेद करते है। यदि `angleDBC=70^(@)` और `angleBAC=30^(@)` हो तो `angleBCD` ज्ञात करें। पुनः यदि `AB=BC` हो तो `angleECD` ज्ञात करें।
View Solutionयदि एक चक्रीय चतुर्भुज के विकर्ण उसके शीर्षो से जानेवाले वृत्त के व्यास हो, तो सिद्ध करें कि वह एक आयत होगा।
View Solutionयदि किसी समलम्ब चतुर्भुज की समांतर भुजाएँ बराबर है। तो सिद्ध कीजिए कि वह चक्रीय चतुर्भुज है।
View Solutionसिद्ध करें कि चक्रीय समांतर चतुर्भुज एक आयत होता है।
View SolutionABCD एक समांतर चतुर्भुज है। A, B एवं C से होकर जानेवाला वृत्त (यदि आवश्यक हो तो बढ़ाकर) CD को E बिन्दु पर प्रतिच्छेद करता है। सिद्ध कीजिए कि `AE=AD` है।
View SolutionAC और BD एक वृत्त की जीवाएँ है जो परस्पर E बिन्दु पर एक-दूसरे को समद्विभाजित करती है। सिद्ध कीजिए (i) AC एवं BD व्यास है, (ii) ABCD एक आयत है।
View Solutionसिद्ध करें कि चक्रीय चतुर्भुज के कोणो के समद्विभाजको से बना चतुर्भुज भी चक्रीय चतुर्भुज होता है।
View Solutionसिद्ध करें कि किसी चक्रीय चतुर्भुज के बाह्य वृत्तखंडो में बने चारो कोणो का योगफल 6 समकोण के बराबर होता है।
View Solution`DeltaABC` की समान भुजाओं AB एवं AC पर दो बिन्दु D एवं E इस प्रकार है कि `AD=AE`। सिद्ध करें कि चारो बिन्दु B, C, E एवं D चक्रीय होंगे।
View Solutionदी गई आकृति में `AB=AC` और `AD=AE` है। सिद्ध करें कि DEFG एक चक्रीय चतुर्भुज है।
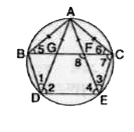
View Solutionकिसी चक्रीय चतुर्भुज ABCD के सम्मुख कोणो `angleA` एवं `angleC` के समद्विभाजक वृत्त को क्रमशः बिन्दु E एवं F बिन्दु पर परिच्छेद करते है। सिद्ध करें कि EF वृत्त का व्यास होगा।
View Solutionसिद्ध करें किसी त्रिभुज के तीनो शीर्षलम्ब एक बिन्दुगामी होते है।
View Solutionबगल की आकृति में `angleA=60^(@),angleABC=80^(@)` है तो `angleDPC` एवं `angleBQC` का मान ज्ञात करें।
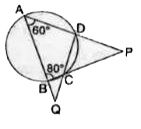
View Solutionदी गई आकृति में दो वृत्त एक-दूसरे को A एवं B बिंदुओं पर प्रतिच्छेद करते है। छोटे वृत्त का केन्द्र, O बिन्दु बड़े वृत्त के परिधि पर स्थित है। यदि PAC तथा PBD दो सरल रेखाएं है तो
(i) `angleAOB` (ii) `angleACB`
(iii) `angleADB` का मान ज्ञात करें।
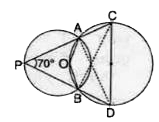
View Solutionकिसी समद्विबाहु `DeltaABC` में `AB=AC` है। B एवं C बिंदुओं से गुजरता हुआ एक वृत्त, भुजा AB एवं AC को क्रमशः D एवं E बिंदुओं पर काटता है। सिद्ध करें कि `DE||BC`.
View Solutionकिसी चक्रीय चतुर्भुज ABCD के विकर्ण एक-दूसरे को P बिन्दु पर लम्बवत प्रतिच्छेद करते है। सिद्ध करें कि P बिन्दु से होकर जानेवाली रेखा जो चक्रीय चतुर्भुज ABCD की एक भुजा को समद्विभाग करती है, पीछे की ओर बढ़ाने पर सम्मुख भुजा पर लम्ब होगी।
View Solution
साधित उदाहरण questions and complete solutions for chapter वृत्त of ALOK BHARATI MATHS (HINDI) of Class 9
All Exercises from ALOK BHARTI PUBLICATION Class 9 MATHS वृत्त
- प्रश्नावली 12.1 (अतिलघु उत्तरीय प्रश्न)
- प्रश्नावली 12.1 (अतिलघु उत्तरीय प्रश्न) रिक्त स्थान
- प्रश्नावली 12.1 (दीर्घ उत्तरीय प्रश्न)
- प्रश्नावली 12.1 (बहुविकल्पीय प्रश्न)
- प्रश्नावली 12.1 (लघु उत्तरीय प्रश्न)
- प्रश्नावली 12.2 (अतिलघु उत्तरीय प्रश्न)
- प्रश्नावली 12.2 (अतिलघु उत्तरीय प्रश्न) रिक्त स्थान
- प्रश्नावली 12.2 (बहुविकल्पीय प्रश्न)
- प्रश्नावली 12.2 (लघु उत्तरीय प्रश्न)
- प्रश्नावली 12.3 (अतिलघु उत्तरीय प्रश्न)
- प्रश्नावली 12.3 (अतिलघु उत्तरीय प्रश्न) रिक्त स्थान
- प्रश्नावली 12.3 (दीर्घ उत्तरीय प्रश्न)
- प्रश्नावली 12.3 (बहुविकल्पीय प्रश्न)
- प्रश्नावली 12.3 (लघु उत्तरीय प्रश्न)
- साधित उदाहरण