Complete Solutions to स्वमूल्यांकन परिक्षण of chapter चतुर्भुर्ज of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | चतुर्भुर्ज |
| BALAJI PUBLICATION | स्वमूल्यांकन परिक्षण |
| Number Of Questions | 29 |
| Academic Year | 2023-24 |
सिद्ध कीजिए की एक समान्तर चतुर्भुर्ज की विपरीत के मध्य बिंदुओं को मिलाने वाली सरल रेखा, समान्तर भुजाओं के अन्य युग्म से समान्तर होती है।
View Solutionएक चतुर्भुर्ज के कोण `3:5:9:13` के अनुपात में है। चतुर्भुर्ज के सभी कोण ज्ञात कीजिए।
View Solutionदर्शाइए की एक वर्ग के विकर्ण बराबर होते है तथा एक-दूसरे को समकोण पर समद्विभाजित करते है।
View Solutionएक समान्तर चतुर्भुर्ज `ABCD` व विकर्ण `AC,angleA` को समद्विभाजित करता है तो सिद्ध कीजिए की-
(i) यह `angleC` को भी समद्विभाजित करता है
(ii) का समचतुर्भुर्ज है।
View SolutionABC के समबाहु त्रिभुज है तथा `L,M,N` क्रमशः भुजाओं `BC,CA` और `AB` के मध्य बिन्दु है तो दर्शाइए की `DeltaLMN` एक समबाहु त्रिभुज है।
View Solutionएक समलम्ब चतुर्भुर्ज `ABCD` इस प्रकार है की `AB||CD` तथा `AD=BC` तो दर्शाइए की
(i) `angleA=angleB (ii) angleC=angleD`
(iii) `DeltaABC~=DeltaBAD`
(iii) विकर्ण `AC=` विकर्ण BD
View Solutionएक समचतुभुर्ज की भुजाओं के मध्य बिंदुओं को मिलाने पर एक चतुर्भुर्ज बनता है। सिद्ध कीजिए की वह एक आयत होगा।
View Solutionएक चतुर्भुर्ज `ABCD` की भुजाओं `AB,BC,CD` और `DA` के मध्य बिन्दु क्रमशः `P,Q,R` और `S` है तथा जिसमे `AC=BD` है तो सिद्ध कीजिए की `PQRS` एक समचतुर्भुज है।
View SolutionABCD एक समचतुर्भुर्ज है जिसमे भुजा ``AB की `D` से ऊँचाई `AB` को समद्विभाजित करती है। तो समचतुर्भुज के कोण ज्ञात कीजिए।
View Solutionएक समान्तर चतुर्भुर्ज के एक अधिक कोण के शीर्ष से, समान्तर की दो ऊंचाइयों के बिच का कोण `60^(@)` है। एक समान्तर चउतुर्भुर्ज के कोण ज्ञात कीजिए।
View Solutionएक चतुर्भुर्ज ABCD है जिसमे ``P,Q,R और `S` क्रमशः भुजाओं `AB,BC,CD` और `DA` के मध्य बिन्दु है `AC` एक विकर्ण है तो दर्शाइए की-
`SR||AC` और `SR=(1)/(2)AC`
(iii) `PQ=SR`
(iii) PQRS एक समान्तर चतुर्भुर्ज है।
View Solutionएक समद्विबाहु समकोण त्रिभुज में एक वर्ग बनाया गया है। वर्ग और त्रिभुज का एक कोण उभयनिष्ठ है। दर्शाइए की उभयनिष्ठ कोण के शीर्ष के विपरीत, वर्ग का शीर्ष कर्ण को समद्विभाजित करता है।
View Solutionएक `DeltaABC` में `D,E` और F क्रमशः भुजाओं `BC,CA` और `AB` के मध्य बिंदु है। यदि भुजाओं `AB,BC` और `CA` की लम्बाईयाँ क्रमशः 7 सेमी, 8 सेमी 9 सेमी है तो दर्शाइए की `Delta DEF` का परिमाप 12 सेमी है ।
View Solutionमाना एक समद्विभाजक त्रिभुज `ABC` इस प्रकार है की AB=AC यदि D,E और F क्रमशः भुजाओं BC,CA और AB के मध्य बिंदू है तो दर्शाइए की रेखाखण्ड AD और EF एक-दूसरे को समकोण पर समद्विभाजित करती है|
View Solutionएक समान्तर चतुर्भुर्ज का परिमाप 22 सेमी है यदि बड़ी भुजा की माप सेमी है दर्शाइए की छोटी भुजा की माप `4.5` सेमी है।
View Solutionयदि एक समान्तर चतुर्भुर्ज के कोण, इसके आसन्न कोण का `(4)/(5)` है। तो समान्तर चतुभुर्ज के कोण ज्ञात कीजिए।
View Solutionसंलग्न चित्र में, एक समान्तर चतुर्भुर्ज `ABCD` है जिसमे `angleA` और `angle B` के समद्विभाजक एक बिंदु P पर प्रतिच्छेद करते है, दर्शाइए की `angleAPB=90^(@)`
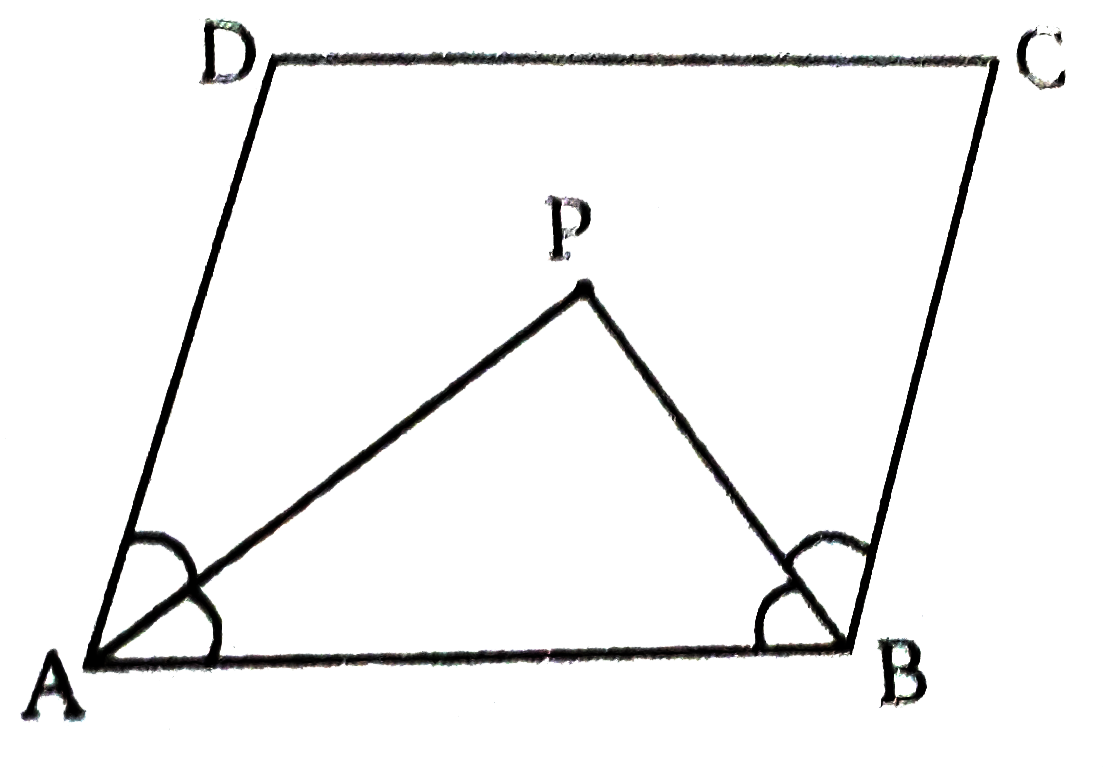
View Solutionसंलग्न चित्र में,`ABCD` एक समान्तर चतुर्भुर्ज है, `E,AB` का मध्य बिंदु है और `CE, angle BCD` को समद्विभाजित करता है। सिद्ध कीजिए की
(i) `AE=AD`
(ii) `DE angle ADC` को समद्विभाजित करता है।
`(iii) angleDEC=90^(@)`
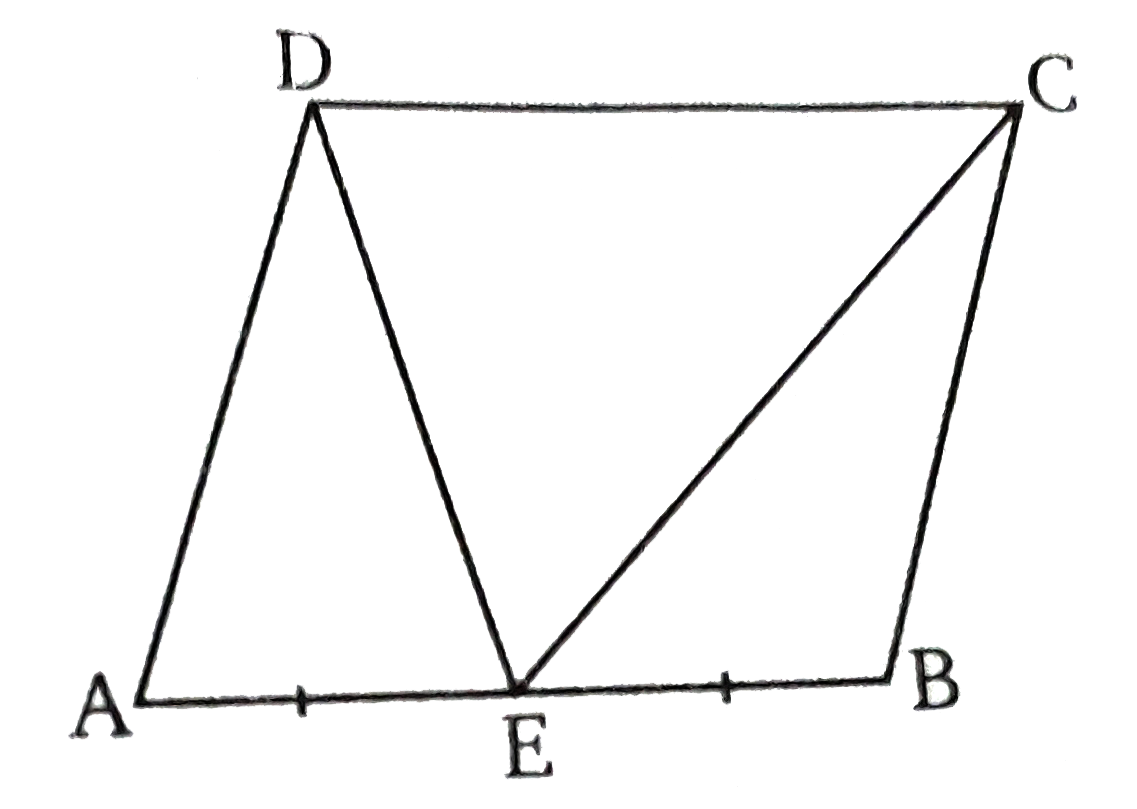
View Solutionयदि एक समान्तर चतुर्भुर्ज एक एक विकर्ण, समान्तर चतुभुर्ज के कोणों में से एक को समद्विभाजित करता है तो सिद्ध कीजिए की यह, इसके विपरीत कोण को भी समद्विभाजित करता है तथा दोनों विकर्ण परस्पर लंबवत है।
View Solutionयदि `ABCD` एक चतुर्भुर्ज है जिसके विकर्ण `AC` और `BD,O` पर परिच्छेद करते है तो सिद्ध कीजिए की :
`(i) (AB+BC+CD+DA)gt (AC+BD)`
(ii) `(AB+BC+CD+DA) lt 2 (AC+BD)`

View Solutionसंलग्न चित्र में , एक बिंदु एक `O` समचतुर्भुर्ज `ABCD` के भीतर इस प्रकार लिया गया है की `OB=OD` तो दर्शाइए की `A,O` और `C` समान रेखा में है।
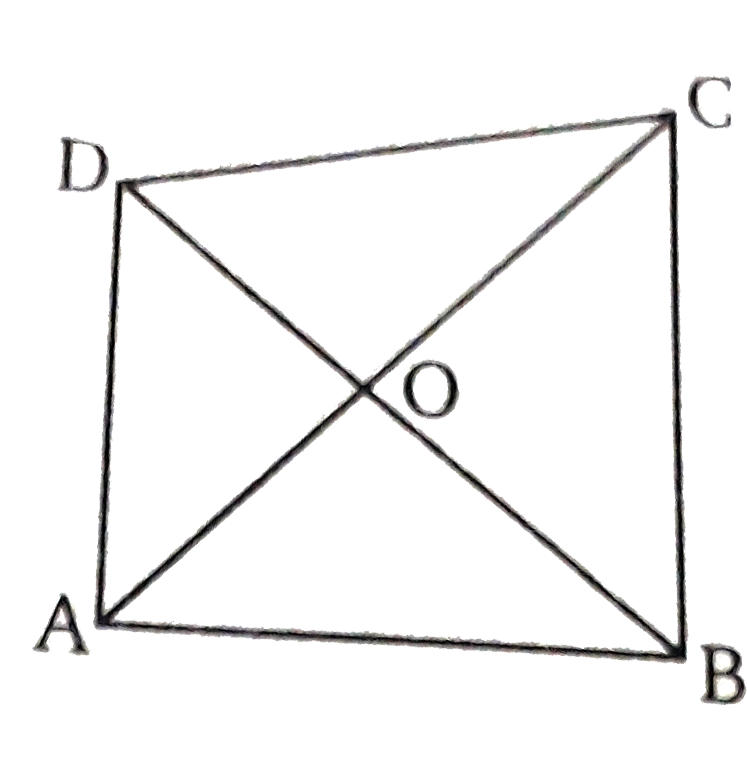
View Solutionएक चतुर्भुज के विकर्ण लंबवत है तो दिखाइए की चतुभुर्जिय आकृति में, इसकी भुजाओ के मध्य बिंदुओं को मिलाने पर प्राप्त आकृति एक आयत है ।
View Solutionसिद्ध कीजिए की एक समान्तर चतुर्भुर्ज के कोणों के समद्विभाजकों द्वारा घिरा क्षेत्र एक आयत है ।
View Solutionएक वर्ग की भुजाओं के मध्य बिंदुओं को मिलाने पर प्राप्त आकृति एक वर्ग होता है।
View Solutionयदि एक तिर्यक दो समान्तर रेखाओं को कटती है तो दर्शाइए की अन्तः कोणों के समद्विभाजक एक आयत बनाते है।
View Solutionसमान्तर चतुर्भुर्ज ABCD के विकर्ण BD को तीन बराबर भागों में बिंदु P व Q से बाँटा जाता है, सिद्ध कीजिए की `CQ,AP` के समान्तर है।
View SolutionABCD एक समान्तर चतुर्भुर्ज है। AD को E तक इस प्रकार बढ़ाया गया है की DE=DC तथा EC का बढ़ा भाग, AB के बढे भाग F में मिलता है तो सिद्ध कीजिए की `BF=BC`
View Solutionएक समान्तर चतुर्भुर्ज ABCD है। E तथा F क्रमशः AB तथा AD के मध्य बिन्दु है । कोई रेखा GH है जो `AD,EF` और BC को क्रमशः G,P और H पर प्रतिच्छेद करती है तो सिद्ध कीजिए की `GP=PH`.
View SolutionABC एक त्रिभुज है तथा A,B और C से, BC,CA और AB समान्तर रेखाएँ खींची गई है जो क्रमशः P,Q तथ R पर प्रतिच्छेद करती है तो सिद्ध कीजिए की `DeltaPQR` का परिमाप, `DeltaABC` के परिमाप का दोगुना है।
View Solution
स्वमूल्यांकन परिक्षण questions and complete solutions for chapter चतुर्भुर्ज of SHREE BALAJI MATHS (HINDI) of Class 9