Complete Solutions to उदाहरण of chapter चतुर्भुर्ज of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | चतुर्भुर्ज |
| BALAJI PUBLICATION | उदाहरण |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |
माना `ABCD` एक समान्तर चतुर्भुर्ज है तथा AP व CQ क्रमशः बिन्दु A व C से विकर्ण पर आएले गए लम्ब है। सिद्ध कीजिए की `AP=CQ`
View Solutionएक चतुर्भुज के कोण` 1:4:2:3:` के अनुपात मे हो तो कोणों के मान ज्ञात कीजिए
View Solutionचित्र में `ABCD` एक समान्तर चतुर्भुज है। x व y के मान ज्ञात कीजिए।
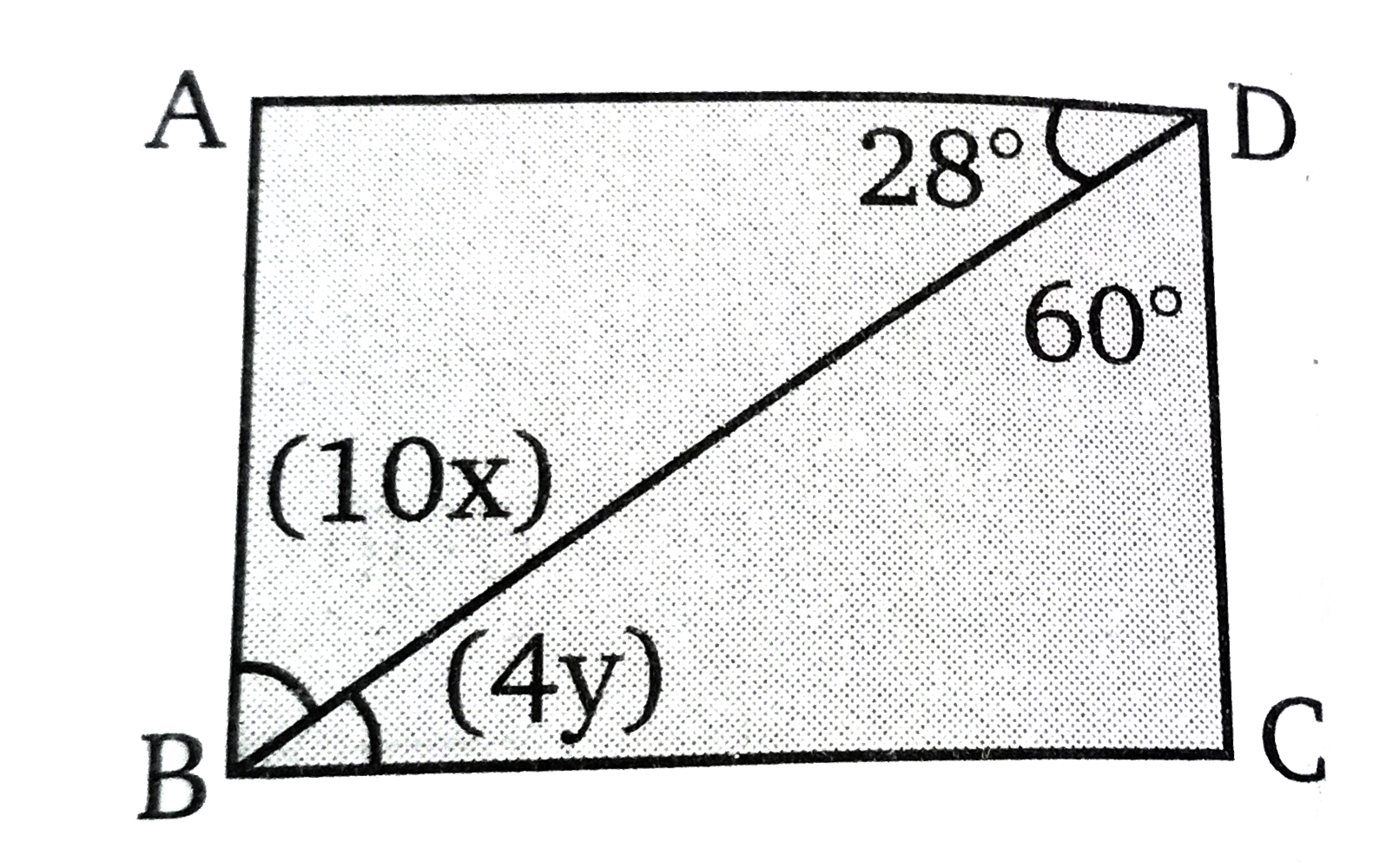
View Solutionकिसी समनांतर चतुर्भुज में यदि विकर्ण एक कोण को समद्विभाजित करता है तो सिद्ध कीजिए की यह प्रमुख कोण को भी समद्विभाजित करता है ।
View Solutionएक चतुर्भुर्ज `ABCD` की भुजाएं BA और DC चित्र `(13.27)` की तरह बनायी गयी है । सिद्ध कीजिए की `a+b=x+y`
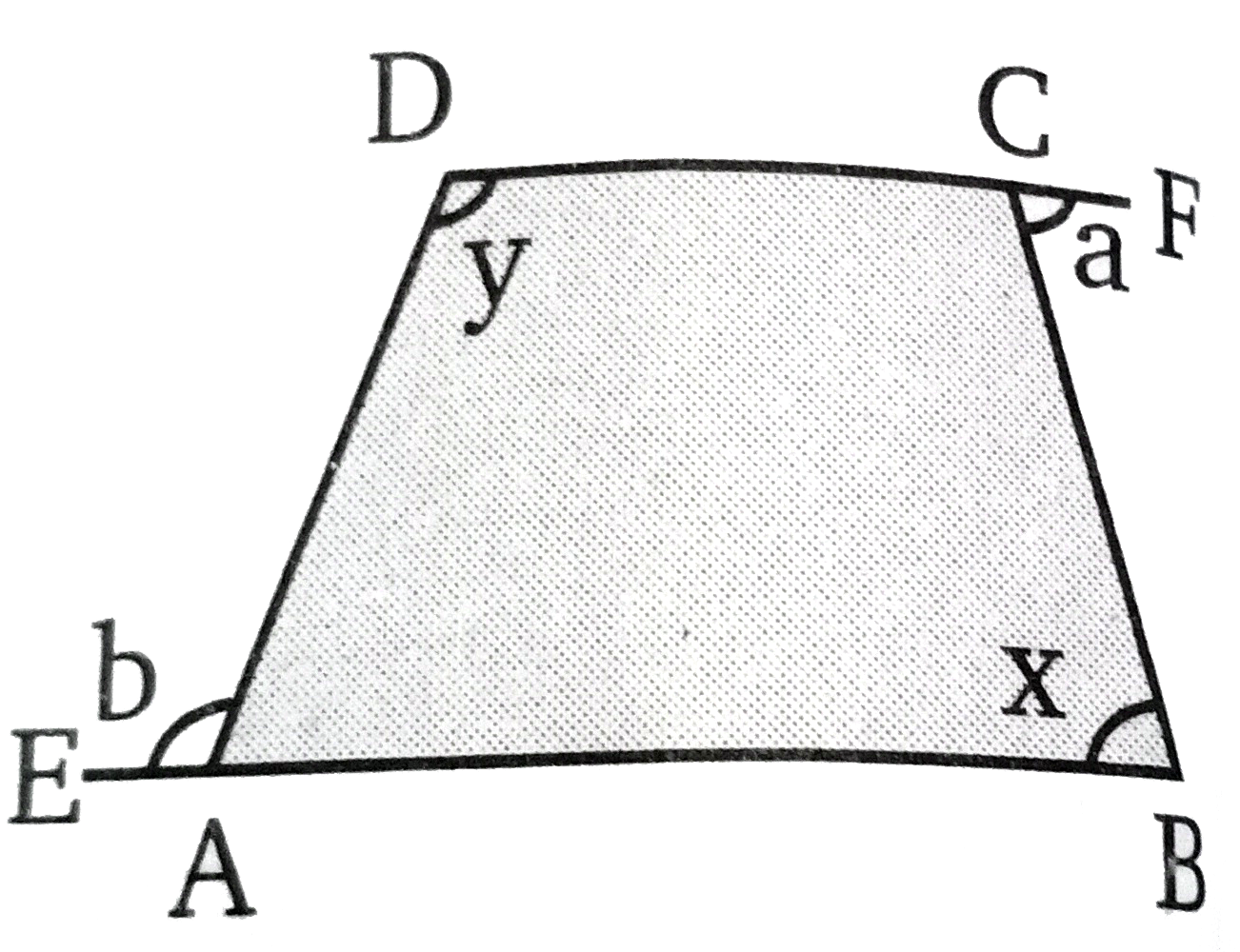
View Solutionचित्र (13.28) में
अतः `OC=3.4` सेमी व `OD=2.8` सेमी
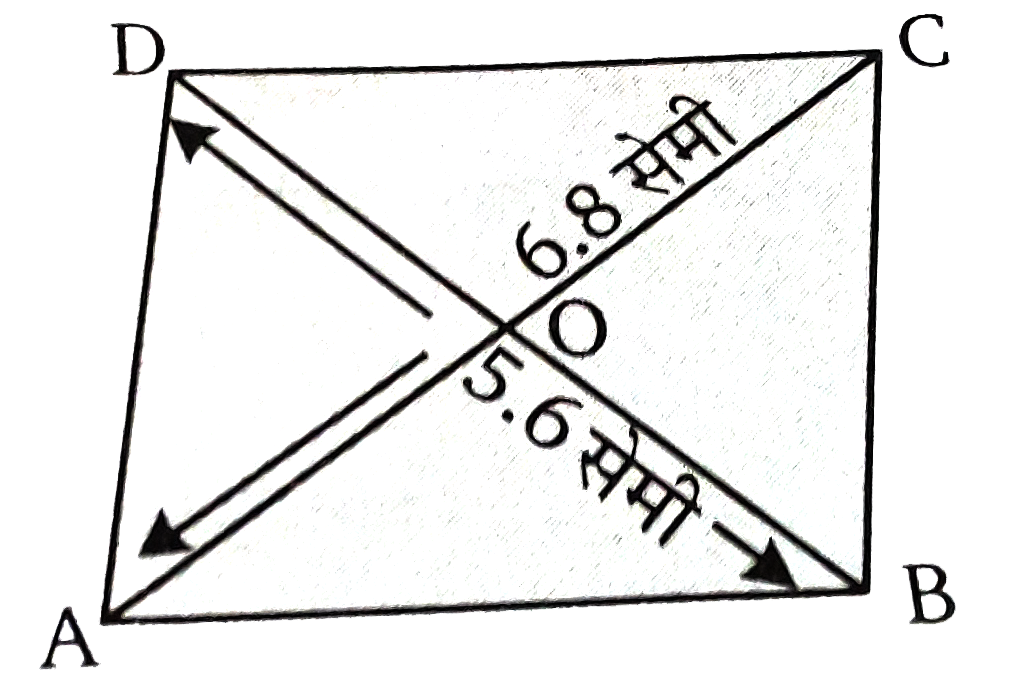 `ABCD` एक समान्तर चतुर्भुर्ज है। जिसके विकर्ण AC व BD बिन्दु O पर प्रतिच्छेद करते है। यदि `AC=6.8` सेमी `BD=5.6` सेमी तब OC व OD की लम्बाई ज्ञात कीजिए।
`ABCD` एक समान्तर चतुर्भुर्ज है। जिसके विकर्ण AC व BD बिन्दु O पर प्रतिच्छेद करते है। यदि `AC=6.8` सेमी `BD=5.6` सेमी तब OC व OD की लम्बाई ज्ञात कीजिए।
View Solutionयदि `ABCD` एक चतुर्भुर्ज है जिसमे `AB||CD` व `AD=BC` सिद्ध कीजिए की `angleA=angleB`
View Solutionदिए गए `DeltaABC,` में `BC,CA` व AB के समान्तर क्रमशः A,B बिन्दु C पर रेखाएँ खींचे तथा `DeltaPQR` बनाये। सिद्ध कीजिए की `BC=(1)/(2)OR`
View Solutionचित्र `(13.31)` में X व Y क्रमशः समान्तर चतुर्भुर्ज ABCD की सम्मुख भुजाओं AB व CD के मध्य बिन्दु है। AY व DX बिन्दु P पर प्रतिच्छेद करती है। तथा CX व BY बिन्दु Q पर प्रतिच्छेद करती है। सिद्ध कीजिए की `PXQY` एक समान्तर चतुर्भुर्ज है।
View SolutionAB व CD दो समान्तर भुजाएँ है। तिर्यक रेखा `l,AB` व `CD` को क्रमशः X व Y पर प्रतिच्छेद करती है। सिद्ध कीजिए की आंतरिक कोण के समद्विभाजक एक आयत बनाते है।
View Solutionचित्र `(13.33)` में ABCD एक समान्तर चतुर्भुर्ज है। विकर्ण BD पर दो बिन्दु X व Y इस प्रकार है की `DX=BY` सिद्ध कीजिए की AXCY एक समान्तर चतुर्भुर्ज है।
View Solutionचित्र `(13.34)` में ABCD एक समान्तर चतुर्भुर्ज है तथा P व Q क्रमशः भुजाओं AB व DC के मध्य बिन्दु है। सिद्ध कीजिए की APCQ एक समान्तर चतुर्भुर्ज है।
View Solutionदो रेखाखण्ड AC व BD बिन्दु P पर समद्विभाजित करते है। सिद्ध कीजिए की `ABCD` एक समान्तर चतुर्भुर्ज है।
View Solutionसंलग्न चित्र में समान्तर चतुर्भुर्ज `ABCD` के विकर्ण `BD` के लंम्बवत AN व CP दो रेखाएं है सिद्ध कीजिए की
(i) `DeltaADN~=DeltaCPB " " (ii) AN=CP`
View Solutionसंलग्न चित्र में ABC एक समद्विबाहु है जिसमे `AB=AC,CP||AB` तथा `AB` के `AP,DeltaABC` बाहय कोण `angleCAD` का अर्द्धक है सिद्ध कीजिए की
(i)`anglePAC=angleBCA`
(ii) `ABCP` एक समान्तर चतुर्भुर्ज है।
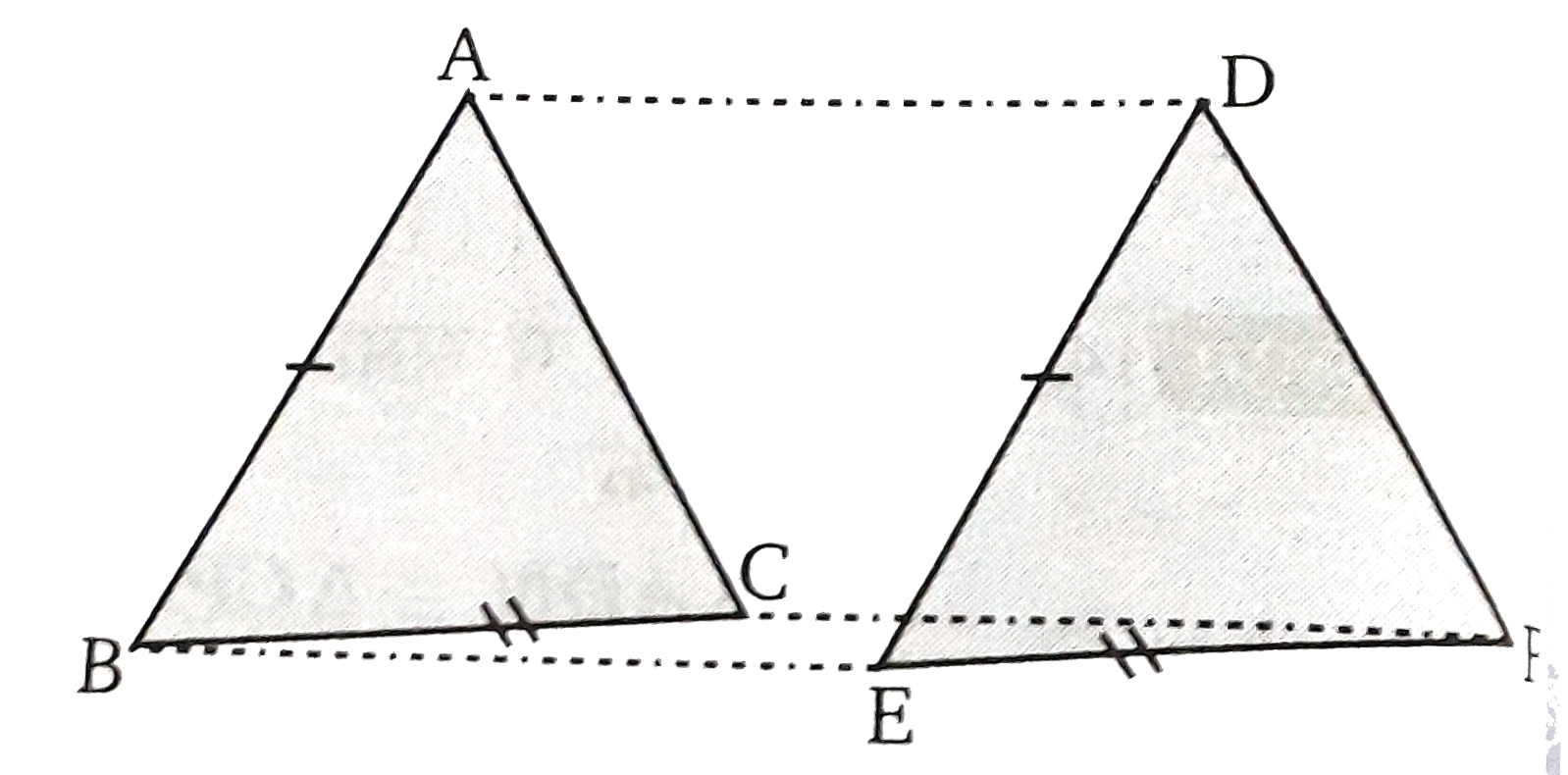
View Solution`DeltaABC` व `DeltaDEF` दो त्रिभुज इस प्रकार है की AB व BC क्रमशः DE व EF के बराबर तथा समान्तर है। सिद्ध कीजिए की
(i) चतुर्भुर्ज `ABED` एक समान्तर चतुर्भुर्ज होगा
(ii) चतुर्भुर्ज `BCEF` एक समान्तर चतुर्भुर्ज होगा
(iii) `AC=DF`
(iv) `DeltaABC~=DeltaEF`
View Solutionसिद्ध कीजिए की समचतृर्भुर्ज की चारों की लम्बाई समान होती है|
View Solutionआयत `ABCD` में विकर्ण `AC, angleA` व `angleC` को समद्विभाजित करता है। सिद्ध कीजिए की
(i) ABCD एक वर्ग है।
(ii) विकर्ण `BD,angleB` व `angleD` को समद्विभाजक करता है।
View Solutionसिद्ध कीजिए की किसी त्रिभुज की क्रमिक भुजाओं के युग्मों के मध्य बिंदुओं को मिलाने वाले रेखाखण्ड से बने चार त्रिभुज सर्वांगसम होते है।
View Solutionचित्र (`13.53)` में D,E व F समबाहु त्रिभुज `ABC` की भुजाएँ क्रमशः `BC,CA` व `AB` के मध्य बिन्दु है। सिद्ध कीजिए की `DeltaDEC` समबाहु त्रिभुज है।
View Solutionत्रिभुज `ABC` में `AD` बिन्दु `A` से माध्यिका है तथा `E,AD` का मध्य बिंदुय है। `BE` को ऐसे बढ़ाते है की यह `AC` से F पर मिलती है । सिद्ध कीजिए की `AF=(1)/(3)AC`
View Solutionसिद्ध कीजिए की किसी आयत की क्रमिक भुजाओं के युग्मों के मध्य बिंदुओं को मिलाने वाले रेखाखण्ड से बना चतुर्भुज एक समचतुर्भुज होता है ।
View Solutionसिद्ध कीजिए की किसी वर्ग की क्रमिक भुजाओं के युग्मों के मध्य बिंदुओं को मिलाने वाले रेखाखण्ड से बना चतुर्भुज भी एक वर्ग होता है।
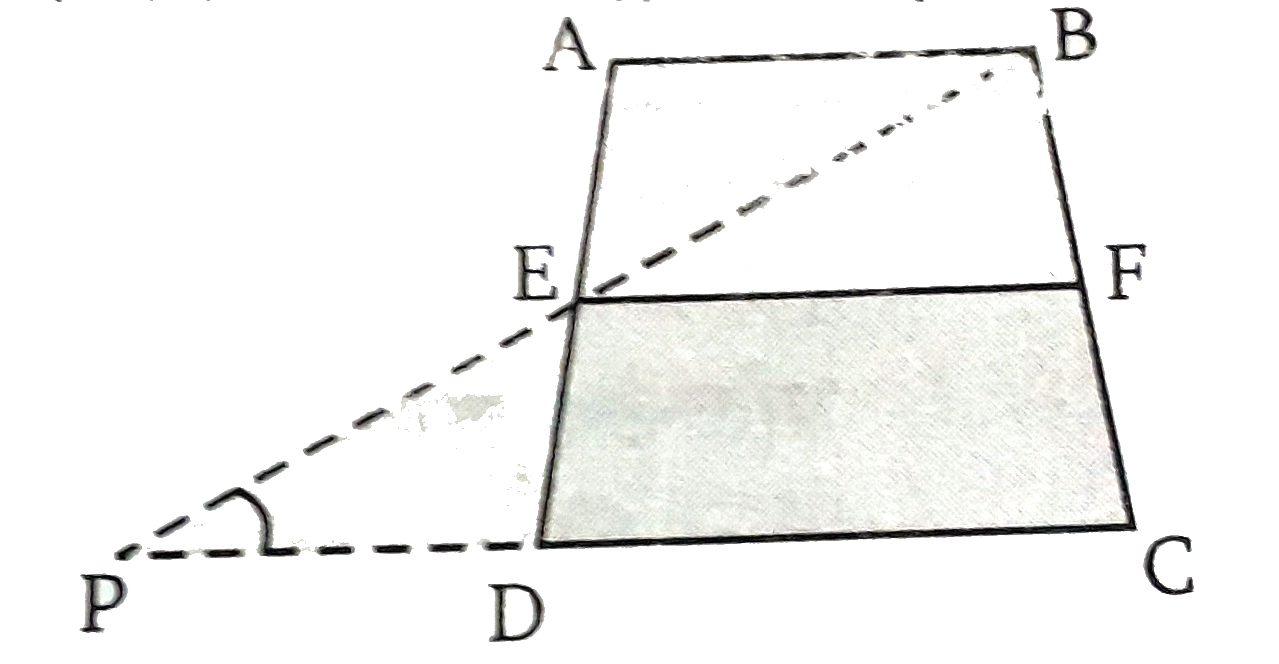
View Solutionचित्र में (13.57) में ABCD समलम्ब चतुर्भुज है । जिसमे AB भुजा DC के समान्तर है तथा E,AD का मध्य बिंदु है। यदि E से भुजा DC के समांतर एक रेखा खींची गई है जो BC को बिंदु F पर प्रतिच्छेद करती है तब सिद्ध कीजिए की `EF=(1)/(2)(AB+BC)`

View SolutionE व F क्रमशः समतल चतुर्भुज `ABCD` की असमान्तर भुजाओं के मध्य बिन्दु है। सिद्ध कीजिए की
(i) `EF||AB `
(ii)` EF=(1)/(2)(AB+CD)`
View Solutionसिद्ध कीजिए की एक समलम्ब चतुर्भुज के विकर्णों के मध्य बिंद्युओं को मिलाने वाले रेखाखण्ड समान्तर भुजाओं के समान्तर उनके अन्तर का आधा होता है ।
View Solutionचित्र `(13.70)` में बिन्दु E समलम्ब चतुर्भुर्ज `ABCD` की भुजा AD का मध्य बिन्दु है तथा `AB||DC,AB` के समान्तर E से एक रेखा `BF` से `F` बिन्दु पर मिलती है । सिद्ध कीजिए की `F,BC` का मध्य बिन्दु है।
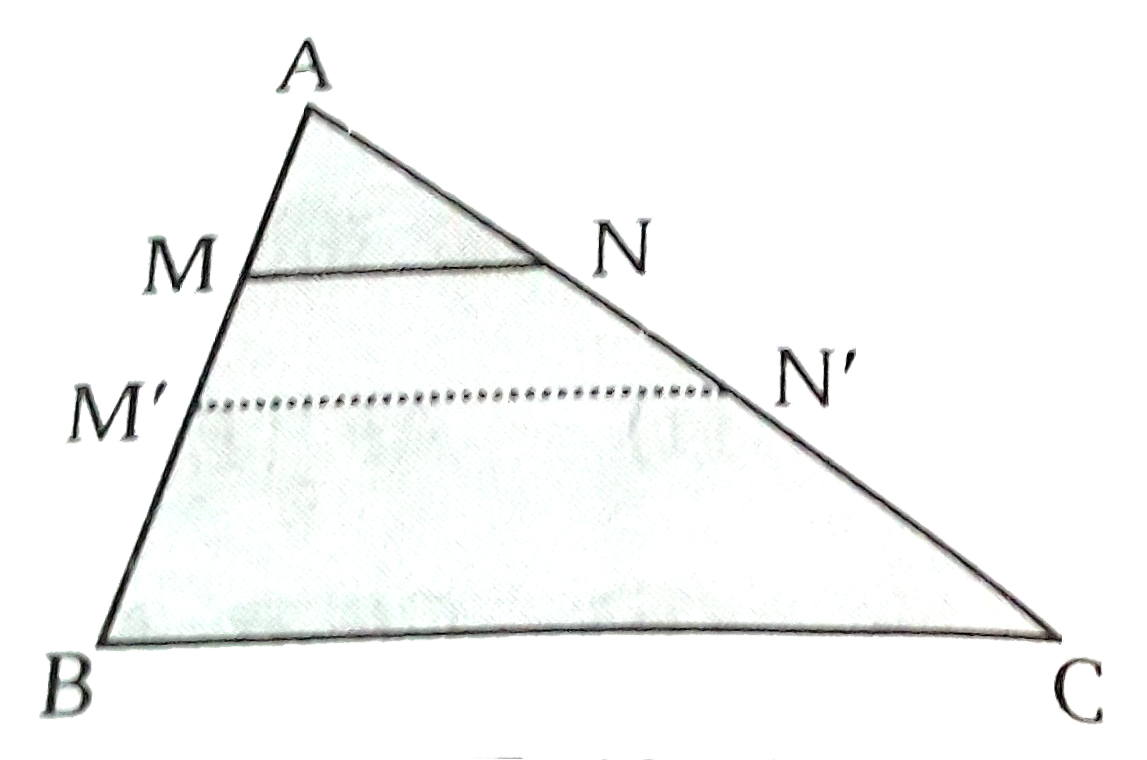
View Solutionत्रिभुज `ABC` में भुजा AB को बिन्दु M व N तीन बराबर भागों में बाँटते है। रेखाखण्ड MP व NQ दोनों BC के समान्तर है और AC को क्रमशः P तथा `Q` पर मिलते है। सिद्ध कीजिए की P व Q भुजा AC को तीन बराबर भागो में बांटते है।
View Solutionचित्र `13.72` में तीन समान्तर रेखाएं l,m व n प्रतिच्छेद रेखा p से क्रमशः बिंदुओं से `A,B` व C पर एवं प्रतिच्छेद रेखा q से क्रमशः D,E व F पर प्रतिच्छेद होती है। अतः `AB:BC=1:2` तो सिद्ध कीजिए की `DE:EF=1:2`
View Solutionचित्र `(13.78)` में `AB||PQ,AB=PQ,AC||PR` व `AC=PR` सिद्ध कीजिए की `BQ||CR` व `BQ=CR`
View Solutionत्रिभुज ABC में बिन्दु M व N क्रमशः AB व AC पर बिन्दु है तथा `AM=(1)/(4)AB` व `=(1)/(4)AC` सिद्ध कीजिए की `MN=(1)/(4)BC`
View SolutionABCD एक समचतुर्भुज है। AB को E व F की ओर इस प्रकार बढ़ाया जाता है `AE=AB=BF`
सिद्ध कीजिए की `ED` व `FC` परस्पर लम्ब है।
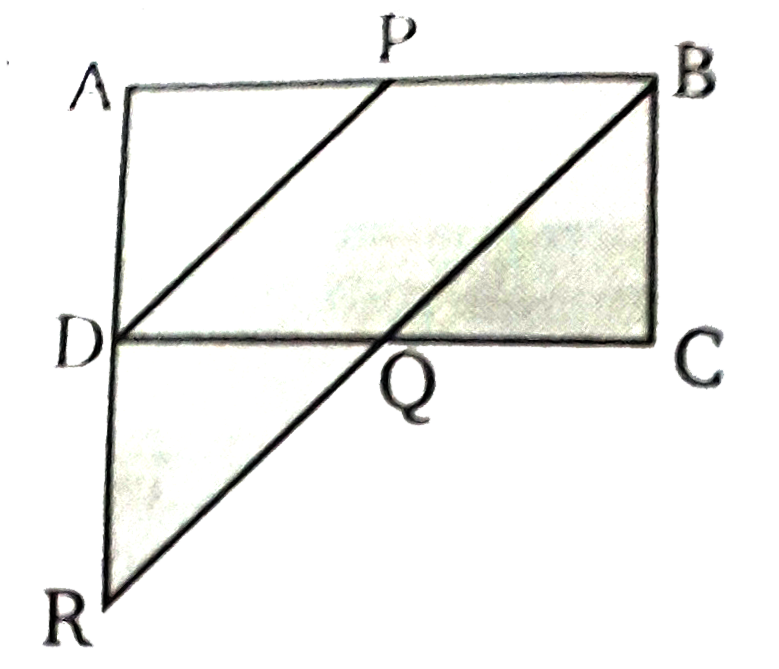
View Solutionएक समान्तर चतुर्भुर्ज `ABCD` में P भुजा AB का मध्य बिन्दु है, B से PD के समान्तर एक रेखा DC से Q पर मिलती है तथा AD को R तक बढ़ाया गया है। तो सिद्ध कीजिए
(i) `AR=2BC " " (ii) BR=2BQ`
View Solutionएक त्रिभुज ABC है जो B पर समकोण है तथा P,AC का माधुय बिन्दु है और तो सिद्ध कीजिए की
(i) `PQ bot AB " " (iii) Q,AB` का मध्य बिन्दु है।
View Solution
उदाहरण questions and complete solutions for chapter चतुर्भुर्ज of SHREE BALAJI MATHS (HINDI) of Class 9