Complete Solutions to साधित उदाहरण of chapter चतुर्भुज of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | चतुर्भुज |
| BHARATI BHAWAN | साधित उदाहरण |
| Number Of Questions | 37 |
| Academic Year | 2023-24 |
एक चतुर्भुज के तीन कोणों की मा क्रमशः `110^(@),82^(@)` तथा `68^(@)` हैं। उसके चौथे कोण की माप ज्ञात कीजिए।
View Solutionएक चतुर्भुज के कोण 3:5:9:13 के अनुपात में हैं। इस चतुर्भुज के सभी कोण ज्ञात कीजिए।
View Solutionएक चतुर्भुज ABCD की भुजाओं BA तथा DC को बढ़ाया गया है जैसा कि संलग्न आकृति में दर्शाया गया है। सिद्ध कीजिए कि `x+y= a + b `है।

View Solutionएक चतुर्भुज ABCD में, ` angle C` तथा `angleD` के समद्विभाजक परस्पर बिंदु E पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि `angleA+ angleB=2angleCED `है।
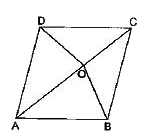
View Solutionसंलग्न आकृति में, एक समबाहु चतुर्भुज ABCD के अंतःभाग में एक बिंदु O इस प्रकार है कि OB = OD है। दर्शाइए कि बिंदुएँ A,O तथा C सरेख हैं।
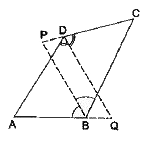
View Solutionसंलग्न आकृति में, एक चतुर्भुज ABCD में ` angle B` तथा `angleD` के समद्विभाजक बढ़ाई गई CD तथा AB को क्रमशः बिंदुओं P और Q पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि ` angle P +angleQ= (1)/(2)(angleB+ angleD).`
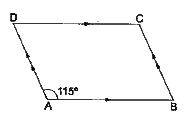
View Solutionएक समांतर चतुर्भुज ABCD में, यदि `angle A=115^(@)` है, तो `angle B ,angle C` तथा `angle D` ज्ञात कीजिए।
View Solutionएक समांतर चतुर्भुज ABCD के विकर्ण AC तथा BD बिंदु O पर प्रतिच्छेद करते हैं। यदि OA = 3 cm तथा OD=2cm है, तो AC तथा BD की लंबाइयाँ ज्ञात कीजिए।
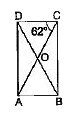
View Solutionआकृति में, ABCD एक आयत है, जिसके विकर्ण AC और BD, बिंदु पर O प्रतिच्छेद कर यदि `angle OCD = 62^(@)` है, तो `angle ODA` ज्ञात कीजिए।
View Solutionसंलग्न आकृति में, ABCD एक समचतुर्भुज है। यदि `angle A=70^(@)` है, तो `angleCDB` ज्ञात करें।
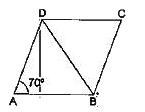
View Solutionकिसी समचतुर्भुज PORS में, विकर्ण PR और QS परस्पर O पर मिलते हैं। यदि `angle PRQ= 50^(@)` है, तो `angle PSQ` ज्ञात कीजिए।
View Solutionसंलग्न आकृति में, ABCD एक वर्ग है। रेखाखंड DP, भुजा BC को P पर प्रतिच्छेद करता है तथा विकर्ण AC को बिंदु O पर इस प्रकार प्रतिच्छेद करता है कि` angle COD=105^(@)` तथा `angle OPC =x^(@)` है। x का मान ज्ञात कीजिए।
View Solutionसंलग्न आकृति में, ABCD एक समांतर चतुर्भुज है तथा इसके विकर्ण BD पर बिंदुएँ x और Y इस प्रकार स्थित हैं कि DX = BY है। सिद्ध कीजिए कि
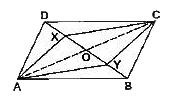
`Delta ADX ~~ Delta CBY` तथा `Delta ABY ~~DeltaCDX, `
View Solutionसंलग्न आकृति में, ABCD एक समांतर चतुर्भुज है तथा इसके विकर्ण BD पर बिंदुएँ x और Y इस प्रकार स्थित हैं कि DX = BY है। सिद्ध कीजिए कि
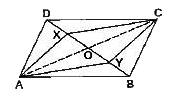
AX =CY तथा CX = AY.
View Solutionसिद्ध कीजिए कि एक समांतर चतुर्भुज में, किन्हीं दो आसन्न कोणों के समद्विभाजक एक समकोण पर प्रतिच्छेद करते हैं।
View Solutionसंलग्न आकृति में, ABCD एक समांतर चतुर्भुज है तथा रेखाखंड AX और CY क्रमशः `angle A` तथा `angle C` के समद्विभाजक हैं। सिद्ध कीजिए कि AX||CY है।
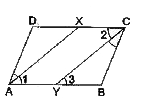
View Solutionसंलग्न आकृति में, ABCD एक समांतर चतुर्भुज है जिसमें X तथा Y क्रमशः AB तथा. DC के मध्यबिंदु हैं। AY तथा DX बिंदु P पर प्रतिच्छेद करते हैं जबकि CX तथा BY बिंदु पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि
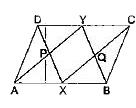
चतुर्भुज AXCY एक समांतर चतुर्भुज है,
View Solutionसंलग्न आकृति में, ABCD एक समांतर चतुर्भुज है जिसमें X तथा Y क्रमशः AB तथा. DC के मध्यबिंदु हैं। AY तथा DX बिंदु P पर प्रतिच्छेद करते हैं जबकि CX तथा BY बिंदु पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि
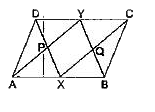
चतुर्भुज XBYD एक समांतर चतुर्भुज है,
View Solutionसंलग्न आकृति में, ABCD एक समांतर चतुर्भुज है जिसमें X तथा Y क्रमशः AB तथा. DC के मध्यबिंदु हैं। AY तथा DX बिंदु P पर प्रतिच्छेद करते हैं जबकि CX तथा BY बिंदु पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि
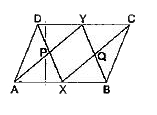
चतुर्भुज PXQY एक समांतर चतुर्भुज है।
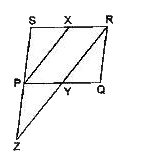
View Solutionसंलग्न आकृति में, एक समांतर चतुर्भुज PORS की भुजा RS का मध्यबिंदु X है। R से होकर PX के समांतर खींची गई रेखा PQ को Y पर तथा बढ़ाई गई SP को Z पर प्रतिच्छेद करती है। दर्शाइए कि PS = PZ और RY=YZ है।
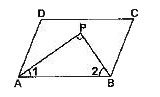
View Solutionसंलग्न आकृति में, AB = AC,CP || BA तथा AP, `angle CAD` का समद्विभाजक है। सिद्ध कीजिए कि
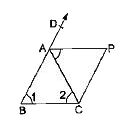
`angle PAC = angle BCA`
View Solutionसंलग्न आकृति में, AB = AC,CP || BA तथा AP, `angle CAD` का समद्विभाजक है। सिद्ध कीजिए कि
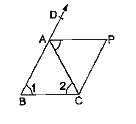
ABCP एक समांतर चतुर्भुज है।
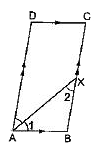
View Solutionसंलग्न आकृति में, ABCD एक समांतर चतुर्भुज है तथा `angle A ` का समद्विभाजक भुजा BC को बिंदु X पर समद्विभाजित करता है। सिद्ध कीजिए कि AD=2AB है।
View Solutionसंलग्न आकृति में, ABCD एक समांतर चतुर्भुज है, E, AB का मध्यबिंदु है तथा `CE, angle BCD `को समद्विभाजित करता है। सिद्ध कीजिए कि
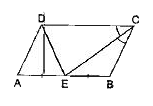
`AE = AD`
View Solutionसंलग्न आकृति में, ABCD एक समांतर चतुर्भुज है, E, AB का मध्यबिंदु है तथा `CE, angle BCD `को समद्विभाजित करता है। सिद्ध कीजिए कि
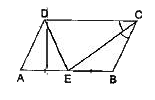
`DE, angle ADC` का समद्विभाजक है,
View Solutionसंलग्न आकृति में, ABCD एक समांतर चतुर्भुज है, E, AB का मध्यबिंदु है तथा `CE, angle BCD `को समद्विभाजित करता है। सिद्ध कीजिए कि
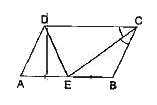
`angle DEC = 90^(@)`
View SolutionABCD एक समलंब है, जिसमें AB || DC और AD = BC है। दर्शाइए कि
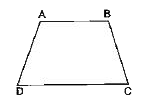
`angle A = angle B` तथा `angle = angle D.`
View SolutionABCD एक समलंब है, जिसमें AB || DC और AD = BC है। दर्शाइए कि
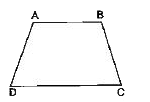
`Delta ABC ~~ Delta BAD,`
View SolutionABCD एक समलंब है, जिसमें AB || DC और AD = BC है। दर्शाइए कि
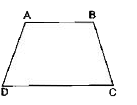
विकर्ण AC = विकर्ण BD.
View Solutionमाना ABC एक त्रिभुज है जिसमें `angle B` एक समकोण है तथा D, AC का मध्यबिंदु है। दर्शाइए कि DA = DB = DC है।
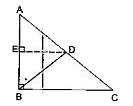
View Solutionयदि E तथा F क्रमशः एक समलंब ABCD की असमांतर भुजाओं AD और BC के मध्यबिंदु हैं, तो सिद्ध कीजिए कि `(i) EF || AB `तथा `(ii) EF= (1)/(2)(AB+ CD).`
View SolutionABCD एक समलंब है जिसमें AB ||DC है। E,भुजा AD का मध्यबिंदु है। E से होकर एक रेखा AB के समांतर खींची गई है, जो BC को F पर प्रतिच्छेद करती है। दर्शाइए कि F, भुजा BC का मध्यबिंदु है तथा `EF = (1)/(2) (AB+ DC)` है।
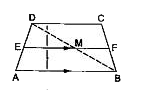
View Solutionसिद्ध कीजिए कि किसी समलंब के विकर्णों के मध्यबिंदुओं को मिलानेवाला रेखाखंड उस समलंब की समांतर भुजाओं के समांतर तथा उनकी लंबाइयों के अंतर के आधे के बराबर होता है।
View SolutionACB एक त्रिभुज है जिसमें `angle C` एक समकोण है। कर्ण AB के मध्यबिंदु P से होकर एक रेखा BC के समांतर खींची गई है, जो AC को M पर प्रतिच्छेद करती है। दर्शाइए कि
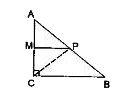
`MP bot AC`
View SolutionACB एक त्रिभुज है जिसमें `angle C` एक समकोण है। कर्ण AB के मध्यबिंदु P से होकर एक रेखा BC के समांतर खींची गई है, जो AC को M पर प्रतिच्छेद करती है। दर्शाइए कि
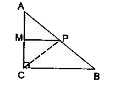
`CP = AP = (1)/(2)AB `
View Solutionसंलग्न आकृति में, AD, `Delta ABC` की माध्यिका है तथा E, AD का मध्यबिंदु है। BE बढ़ाने पर AC को बिंदु F पर प्रतिच्छेद करता है। सिद्ध' कीजिए कि `AF = (1)/(3)AC `है।
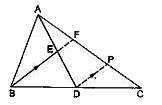
View Solutionसंलग्न आकृति में, D, E तथा Fक्रमशः `Delta ABC` की भुजाओं BC, CA तथा AB के मध्यबिंदु हैं। यदि BE और DF बिंदु X पर तथा CF और DE बिंदु Y पर प्रतिच्छेद करते हैं, तो सिद्ध कीजिए कि `XY =(1)/(4)BC `है।
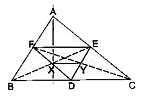
View Solution
साधित उदाहरण questions and complete solutions for chapter चतुर्भुज of BHARATI BHAWAN of Class 9