संलग्न आकृति में, ABCD एक समांतर चतुर्भुज है जिसमें X तथा Y क्रमशः AB तथा. DC के मध्यबिंदु हैं। AY तथा DX बिंदु P पर प्रतिच्छेद करते हैं जबकि CX तथा BY बिंदु पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि
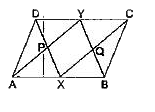
चतुर्भुज XBYD एक समांतर चतुर्भुज है,
The correct Answer is:एक समान्तर चतुर्भुज है
Topper's Solved these Questions
Similar Questions
एक चतुर्भुज के तीन कोणों की मापें क्रमशः 75∘,90∘ तथा 75∘ हैं। उसके चौथे कोण की माप ज्ञात कीजिए।
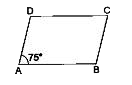
View Solutionदी गई आकृति में, चतुर्भुज ABCD में AB∣∣DC तथा AB=DC=8cmहै। यदि ∠A=75∘ है, तो अन्य कोणों की मा ज्ञात कीजिए।
View Solutionरूलर तथा परकार की सहायता से कोणों की रचना कीजिए।
45∘
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए , जो रेखाओ x+y=3 तथा 2x+3y=7 के प्रतिच्छेद बिंदु को रेखाओ 2x+3y=8 तथा 3x−y=1 के प्रतिच्छेद बिंदु से मिलती है ।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionसिद्ध कीजिए कि बिंदु (1,−6),(5,2),(7,0) तथा (−1,−4)एक चक्रीय चतर्भुज के शीर्ष है ।
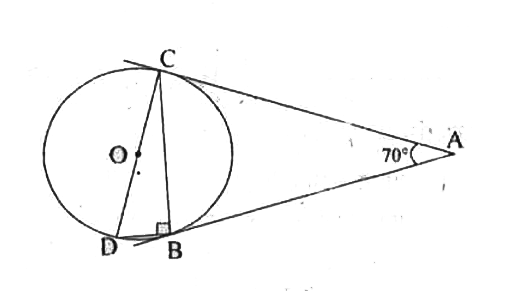
View Solutionदी गई आकृति में बिंदु B ,C तथा D से गुजरने वाले वृत्त के बिंदु B तथा C पर AB तथा AC स्पर्श रेखाएं है। यदि ∠BAC=70∘ और ∠CBD=90∘ तो ∠BCD का मान है -
View Solutionकिसी समांतर चतुर्भुज ABCD में यदि −−→AB=¯a तथा −−→BC=¯b तो सिद्ध कीजिए कि
−−→AC=¯a+¯b और −−→BD=¯b−¯a.
View Solutionसदिशों के प्रयोग द्वार सिद्ध कीजिए कि बिंदु A(−2,3,5),B(7,0,−1),C(−3,−2,−5) और D(3,4,7) इस प्रकार हैं कि AB और CD बिंदु P(1,2,3) पर प्रतिच्छेद करते हैं।
View Solutionसिध्द कीजिए कि सम्मिश्र संख्याओं 6−i,7+3i,8+2i और 7 - 2i को निर्मित करने वाले बिंदु एक समांतर चतुर्भुज बनाते हैं ।
View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View Solutionसमांतर चतुर्भुज का क्षेत्रफल |सूत्र तथा अभ्यास प्रश्न
View SolutionRevision|चतुर्भुज#!#समांतर चतुर्भुज#!#प्रमेय पर आधारित महत्वपूर्ण प्रश्न
View SolutionRevision |कुछ विशिष्ट समांतर चतुर्भुज #!#आयत , वर्ग तथा समचतुर्भुज
View Solutionसदिशों के योग का त्रिभुज तथा समांतर चतुर्भुज नियम
View Solution
