Complete Solutions to साधित उदाहरण of chapter समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल |
| BHARTI_BHAWAN | साधित उदाहरण |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |
WXYZ एक समांतर चतुर्भुज है, जिसमें `XP bot WZ `और `ZQ bot WX` है। यदि `WX = 10cm, XP = 8 cm` और `ZQ=6cm ` है, तो YX ज्ञात कीजिए।
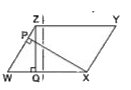
View SolutionABCD एक समलंब है जिसकी भुजा AB पर कोई बिंदु E है। यदि AD || EC और DE || BC है, तो `ar( Delta DAE) : ar(DeltaBEC)` ज्ञात कीजिए।
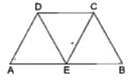
View Solutionदी गई आकृति में, ABCD एक समांतर चतुर्भुज है। बिंदुएँ P और q भुजा BC को तीन बराबर भागों में विभाजित करते हैं। सिद्ध कीजिए कि
`ar (Delta APQ) =ar (DeltaDPQ) = (1)/(6) ra (ABCD).`
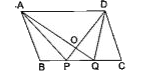
View SolutionD, E और F क्रमशः त्रिभुज ABC की भुजाओं BC,CA और AB के मध्यबिंदु हैं। दर्शाइए कि
`ar (Delta DEF) = (1)/(4) ar (DeltaABC)`
View SolutionD, E और F क्रमशः त्रिभुज ABC की भुजाओं BC,CA और AB के मध्यबिंदु हैं। दर्शाइए कि
`ar (||gm BDEF) = (1)/(2) ar (Delta ABC).`
View Solutionचतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि `ar (Delta APB) xx ar (DeltaCPD) = ar (Delta APD) xx ar ( DeltaBPC).`
View Solutionयदि किसी चतुर्भुज की भुजाओं के मध्यबिंदुओं को क्रम से मिलाया जाता है, तो सिद्ध कीजिए कि इस प्रकार बना चतुर्भुज एक समांतर चतुर्भुज होता है तथा उसका क्षेत्रफल दिए हुए चतुर्भुज के क्षेत्रफल का आधा होता है।
View Solutionसंलग्न आकृति में, चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि OB = OD है। यदि AB = CD है, तो दर्शाइए कि
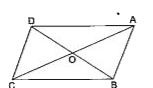
`ar (Delta DOC) = ar ( DeltaAOB)`
View Solutionसंलग्न आकृति में, चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि OB = OD है। यदि AB = CD है, तो दर्शाइए कि
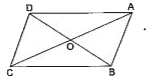
`ar (DeltaDCB) =ar (DeltaACB)`
View Solutionसंलग्न आकृति में, चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि OB = OD है। यदि AB = CD है, तो दर्शाइए कि
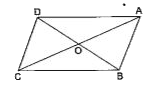
`DC||AB` या ABCD एक समांतर चतुर्भुज है।
View Solutionएक किसान के पास समांतर चतुर्भुज PQRS के रूप का एक खेत था। उसने RS पर स्थित कोई बिंदु A लिया और उसे P और Q से मिला दिया। खेत कितने भागों में विभाजित हो गया है? इन भागों के आकार क्या हैं? वह किसान खेत में गेहूँ और दाल बराबर-बराबर भागों में अलग-अलग बोना चाहता है। वह ऐसा कैसे करे?
View Solutionसंलग्न आकृति में, ABC एक समकोण त्रिभुज है जिसका कोण A समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमशः भुजाओं BC, CA और AB पर बने वर्ग हैं। रेखाखंड `AX bot DE` भुजा BC से बिंदु Y पर मिलता है। दर्शाइए कि
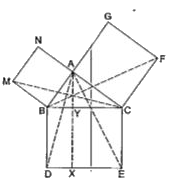
`Delta MBC ~~Delta ABD,`
View Solutionसंलग्न आकृति में, ABC एक समकोण त्रिभुज है जिसका कोण A समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमशः भुजाओं BC, CA और AB पर बने वर्ग हैं। रेखाखंड `AX bot DE` भुजा BC से बिंदु Y पर मिलता है। दर्शाइए कि
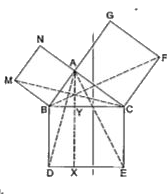
ar (आयत AYXD)`=2 ar (Delta MBC),`
View Solutionसंलग्न आकृति में, ABC एक समकोण त्रिभुज है जिसका कोण A समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमशः भुजाओं BC, CA और AB पर बने वर्ग हैं। रेखाखंड `AX bot DE` भुजा BC से बिंदु Y पर मिलता है। दर्शाइए कि
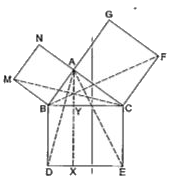
ar (आयत BYXD) =ar (वर्ग ABMN),
View Solutionसंलग्न आकृति में, ABC एक समकोण त्रिभुज है जिसका कोण A समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमशः भुजाओं BC, CA और AB पर बने वर्ग हैं। रेखाखंड `AX bot DE` भुजा BC से बिंदु Y पर मिलता है। दर्शाइए कि
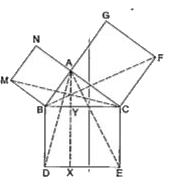
`Delta FCB~~ DeltaACE,`
View Solutionसंलग्न आकृति में, ABC एक समकोण त्रिभुज है जिसका कोण A समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमशः भुजाओं BC, CA और AB पर बने वर्ग हैं। रेखाखंड `AX bot DE` भुजा BC से बिंदु Y पर मिलता है। दर्शाइए कि
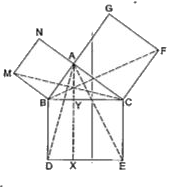
ar (आयत XYXE)= `2ar (Delta FCB),`
View Solutionसंलग्न आकृति में, ABC एक समकोण त्रिभुज है जिसका कोण A समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमशः भुजाओं BC, CA और AB पर बने वर्ग हैं। रेखाखंड `AX bot DE` भुजा BC से बिंदु Y पर मिलता है। दर्शाइए कि
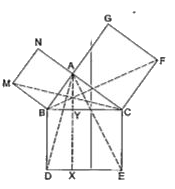
ar(वर्ग BCED) = ar (वर्ग ABMN) + ar (वर्ग ACFG).
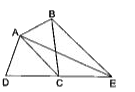
View Solutionसंलग्न आकृति में, ABCD एक चतुर्भुज है और BE || AC इस प्रकार है कि BE बढ़ाई गई DC से E पर मिलती है। दर्शाइए कि त्रिभुज ADE का क्षेत्रफल चतुर्भुज ABCD के क्षेत्रफल के बराबर है।
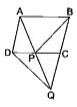
View Solutionदी गई आकृति में, ABCD एक समांतर चतुर्भुज है और BC को एक बिंदु Q तक इस प्रकार बढ़ाया गया है कि, AD = CQ है। यदि AQ भुजा DC को P पर प्रतिच्छेद करती है, तो दर्शाइए कि `ar( Delta BPC) = ar(Delta DPO)` है।
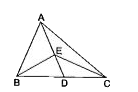
View Solutionदी गई आकृति में, `Delta ABC` की एक माध्यिका AD पर स्थित E कोई बिंदु है। दर्शाइए कि
`ar (Delta BED) = ar (DeltaCDE)`
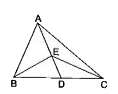
View Solutionदी गई आकृति में, `Delta ABC` की एक माध्यिका AD पर स्थित E कोई बिंदु है। दर्शाइए कि
`ar (Delta ABE) = ar (DeltaACE)`
View Solutionएक चतुर्भुज ABCD में, M, विकर्ण.AC का मध्यबिंदु है। सिद्ध कीजिए कि ar(चतुर्भुज ABMD) = ar(चतुर्भुज DMBC).
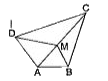
View Solutionयदि `Delta ABC` की माध्यिकाएँ बिंदु G पर प्रतिच्छेद करती हैं, तो दर्शाइए कि` ar( Delta AGB) = ar(DeltaAGC) = ar(DeltaBGC) = =ar(DeltaABC)` है।
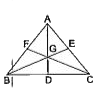
View Solution'यदि किसी चतुर्भुज का प्रत्येक विकर्ण उसे समान क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करता है, तो सिद्ध कीजिए कि वह चतुर्भुज एक समांतर चतुर्भुज है।
View Solutionसंलग्न आकृति में, ABCDE एक पंचभुज है। B से होकर AC के समांतर खींची गई रेखा बढ़ाए गए DC से F पर मिलती है। दर्शाइए कि
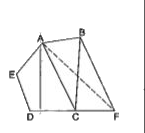
`ar (Delta ACB) = ar ( DeltaACF)`
View Solutionसंलग्न आकृति में, ABCDE एक पंचभुज है। B से होकर AC के समांतर खींची गई रेखा बढ़ाए गए DC से F पर मिलती है। दर्शाइए कि
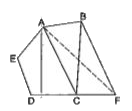
`ar( AEDF) = ar ( ABCDE)`
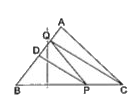
View Solution`Delta ABC `में, D भुजा AB का मध्यबिंदु है तथा P भुजा BC पर स्थित कोई बिंदु है। यदि रेखाखंड CQ || PD भुजा AB से Q पर मिलता है, तो सिद्ध कीजिए कि `ar(DeltaBPQ) =(1)/(2) ar(DeltaABC)` है।
View Solutionएक समलंब ABCD, जिसमें AB ||DC है, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं। दर्शाइए कि `ar( Delta AOD) = ar(DeltaBOC) `है।
View Solutionचतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि `ar( Delta AOD) = ar(DeltaBOC) `है। सिद्ध कीजिए कि ABCD एक समलंब है।
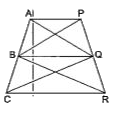
View Solutionसंलग्न आकृति में, AP || BQ || CR है। सिद्ध कीजिए कि `ar( Delta AQC)=ar(DeltaPBR)` है।
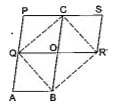
View Solutionसंलग्न आकृति में, PQRS तथा PABC बराबर क्षेत्रफलों के दो समांतर चतुर्भुज हैं। सिद्ध कीजिए कि QC || BR है।
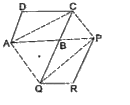
View Solutionसमांतर चतुर्भुज ABCD की एक भुजा AB को एक बिंदु Pतक बढ़ाया गया है। Aसे होकर CP के समांतर खींची गई रेखा बढ़ाई गई CB से Qपर मिलती है और फिर समांतर चतुर्भुज PBOR को पूरा किया गया है।
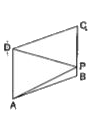
View Solutionसंलग्न आकृति में, ABCD एक समांतर चतुर्भुज है तथा Pभुजा BC पर स्थित एक बिंदु है। सिद्ध कीजिए कि
`ar(Delta ABP) +ar (DeltaDPC) =ar (DeltaPDA).`
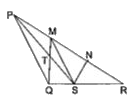
View Solutionएक त्रिभुज PQR की भुजा PR पर दो बिंदु M और N इस प्रकार हैं कि PM = MN = NR है। PQ के समांतर एक रेखा Mसे होकर भुजा QR को S पर प्रतिच्छेद करती है। सिद्ध कीजिए कि `ar( Delta PSN) = ar(DeltaSNM) `
View Solution
साधित उदाहरण questions and complete solutions for chapter समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल of BHARATI BHAWAN of Class 9