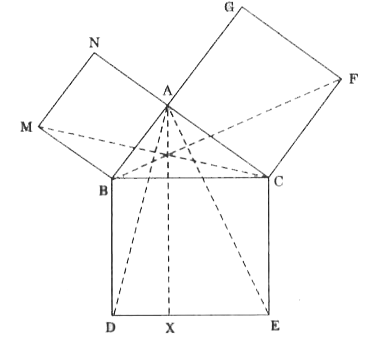
संलग्न आकृति में, ABC एक समकोण त्रिभुज है जिसका कोण A समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमशः भुजाओं BC, CA और AB पर बने वर्ग हैं। रेखाखंड AX⊥DE भुजा BC से बिंदु Y पर मिलता है। दर्शाइए कि
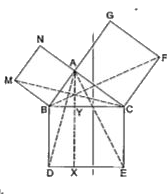
ar (आयत AYXD)=2ar(ΔMBC),
The correct Answer is:ΔABD
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:BHARATI BHAWANChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:प्रश्नमाला 11A
Explore 17 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:BHARATI BHAWANChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:प्रश्नमाला 11B
Explore 2 Videos
- संख्या पद्धति Book:BHARATI BHAWANChapter:संख्या पद्धति Exercise:प्रश्नमाला 1H (बहुवैकल्पिक प्रश्न)
Explore 45 Videos
- सांख्यिकी Book:BHARATI BHAWANChapter:सांख्यिकी Exercise:प्रश्नमाला 16 E
Explore 28 Videos
Similar Questions
नीचे दिए गए आकृतियों में से कौन-सी आकृतियाँ एक ही आधार पर और एक ही समांतर रेखाओं के बीच स्थित है? ऐसी स्थिति में, उभयनिष्ठ आधार और दोनों समांतर रेखाएँ लिखिए।
View Solutionएक समांतर चतुर्भुज ABCD की भुजा AB का मध्यबिंदु M है। यदि ar(AMCD)=24cm2है, तो ar(ΔABC) ज्ञात कीजिए।
View Solutionनिम्नलिखित में से कौन सी संख्या परिमेय है ?
View Solutionआँकड़ो 12,,25,15,18,17,20,22,6,16,11,8,19,10,30,20,32 का परिसर है
View Solutionत्रिभुज ABC में कोण C समकोण है । यदि बिंदु A और B निर्देशांक क्रमशः (−3,4) और (3,−4)हो , तो सिद्ध कीजिये की ΔABC के परिवृत्त का समीकरण x2+y2=25 होगा ।
View SolutionIn the following figure , ABC is a right triangle right angled at A. BCED ACFG and ABMN and squares on the sides BC, CA and AB respectively , Line segement AX ⊥ DE meets BC at Y. Show that
(i) ti⟩MBC=ti⟩(MBC)
(ii) ar (BXYD) = 2 ar (MBC)
(iii) ar (BYXD) = ar(ABMN)
(iv) ti⟩FCB=ti⟩ACE
(v) ar (CYXE) = 2 ar (FCB)
(vi) ar (CYXE ) = ar (ACFG)
(vii) ar (BCED) = ar (ABMN) + ar (ACFG)
View Solutiontriangle ABC में, जिसका B कोण समकोण है, AB = 12 cm और BC = 5 cm है। sin C का मान है :
View Solution△ ABC में, जिसका कोण B समकोण है, AB = 5 cm और, BC = 12 cm है। cos C का मान है :
View SolutionABC is a right angled triangle, right angled at A. A circle is inscribed in it. The lengths of two sides containing the right angle are 48 cm and 14 cm. The radius of the inscribed circle is: ABC एक समकोण त्रिभुज है, A कोण पर समकोण है। समकोण वाले दो भुजाओं की लंबाई 48 सेमी और 14 सेमी है। अन्तर्निहित वृत्त की त्रिज्या है
View SolutionIn triangle ABC , AD bisects angle A and intersects BC at D. If BC = a ,AC = b and AB = c, then BD = ? त्रिभुज ABC में, AD कोण A को समद्विभाजित करता है तथा BC को D पर काटता है | यदि BC = a, AC = b और AB = c है, तो BD = ?
View SolutionIn triangle ABC , angle A is a right angle. The lengths of AC and BC 6 cm and 10 cm respectively. Point D is on AB such that BD = 4 cm. What is the length of CD? त्रिभुज ABC में, कोण A समकोण है | AC और BC की लंबाई क्रमशः 6 सेमी और 10 सेमी है | बिंदु D, AB पर इस प्रकार स्थित है कि BD = 4 सेमी है | CD की लंबाई ज्ञात करें |
View SolutionIn triangle ABC ,AD bisects angle A which meets BC at D. If BC = a, AC = b and AB = c, then DC = ? त्रिभुज ABC में, AD कोण A को द्विभाजित करता है जो BC से D पर मिलता है | यदि BC = a, AC = bऔर AB = c है, तो DC = ?
View SolutionIn △ABC ,P is a point on BC such that BP : PC = 3 : 4 and Q is the midpoint of BP. Then ar(△ABQ):ar(△ABC) is equal to:
त्रिभुज ABC में, P, BC पर स्थित एक ऐसा बिंदु है कि BP : PC = 3 : 4 है और Q, BP का मध्य बिंदु है | ar(△ABQ):ar(△ABC) का मान ज्ञात करें |
View SolutionIn △ABC ,P is a point on BC such that BP : PC = 4:5 and Q is the midpoint of BP. Then ar(△ABQ):ar(△ABC) is equal to:
त्रिभुज ABC में, P, BC पर स्थित एक ऐसा बिंदु है कि BP : PC = 4:5 है और Q, BP का मध्य बिंदु है | ar(△ABQ):ar(△ABC) का मान ज्ञात करें |
View SolutionIn △ABC ,P is a point on BC such that BP : PC = 4 : 11 and Q is the midpoint of BP. Then ar(△ABQ):ar(△ABC) is equal to:
त्रिभुज ABC में, P, BC पर स्थित एक ऐसा बिंदु है कि BP : PC = 4 : 11 है और Q, BP का मध्य बिंदु है | ar(△ABQ):ar(△ABC) का मान किसके बराबर होगा ?
View SolutionIn triangle ABC, D and E are two points on the sides AB and AC respectively so that DE || BC and AD/BD =3/4 .The ratio of the area of △ABC to the area of trapezium DECB is :
त्रिभुज ABC में,D और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु है कि DE ||BC है और AD/BD =3/4 है | त्रिभुज ABC के क्षेत्रफल तथा समलम्ब DECB के क्षेत्रफल में अनुपात ज्ञात करें |
View Solution
