Complete Solutions to CONSTRUCTIONS OF POLYGONS of chapter CHAPTER REVISION (STAGE 2) of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | CHAPTER REVISION (STAGE 2) |
| SELINA PUBLICATION | CONSTRUCTIONS OF POLYGONS |
| Number Of Questions | 19 |
| Academic Year | 2023-24 |
Contruct a parallelogram in which diagonals are 6.5 cm and 4 cm long and angle between them is ` 60^(@) `
View SolutionContruct a square ABCD is which
each side = 5 cm
View SolutionContruct a square ABCD is which
diagonals AC = 9 cm
View SolutionContruct a rhombus ABCD is which
each side = 6 cm ` angle B = 45^(@) `
View SolutionConstruct a rhombus ABCD in which
AC = 5.6 cm and BD = 6.3 cm
View SolutionContruct a rectangle ABCD with diagonal AC = 6.6 cm , side BC = 5.2 cm and ` angle B = 60^(@) `
View SolutionThe following diagram shows two parallelogram ABCD and BEFG
Prove that :
Area of ABCD = Area of BEFG.
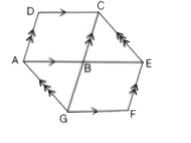
View SolutionIn the parallelogram ABCD , the side AB is produced to the point X.so that BX= AB. The line DX cuts BC at E. Prove that :
DBXC is a parallelogram.
View SolutionIn the parallelogram ABCD , the side AB is produced to the point X.so that BX= AB. The line DX cuts BC at E. Prove that :
Area (`Delta AED) = 2 xx " area " (Delta CEX).`
View SolutionIn the following figure G, is centroid of the triangles ABC.
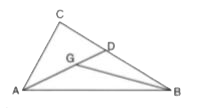
Prove that
Area `(Delta " AGB " )= (1)/(3) xx " Area " (Delta ABC)`
View SolutionUse the informations given in the following figure to show that ar. (ABCQ) = ar (ABCDE)
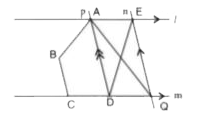
[Given : l // m and p//n ]
View SolutionIf each diagonals of a quadrilateral separates it into two triangles of equal area then show that the quadrilateral is a parallelogram.
View SolutionABCD , ABEF and AGHF are parallelogram
Prove that the area of parallelogram ABCD = area of parallelogram AGHE

View SolutionThe area of the parallelogram ADFE is 275 ` cm ^(2) ` and AD = 12.5 cm . Find the distances between point D and side. EF.
View SolutionProve Equal chords of a circle subtend equal angles at the centre.
View SolutionA line segment AB is length 8 cm . Draw a circle of radius 5 cm that passes thorugh A and B .
Can you draw a circle of radius 3 cm passing through A and B ? Give reason In support of your answer.
View SolutionTwo circles of radii 10 cm and 17 cm . Intersecting each other at two points and the distances between their centres is 21 cm . Find the length of the common chords.
View SolutionIn the given circle. Arc APB and are BQC are in the ratio 2: 5 and O is centre of the circle.

If angle AOB = ` 44^(@) ` : Find angle AOC.
View SolutionIn the given figures , O is the centre of the given circle. AB is a side of a square ,BC
is a side of regular pentagon and CD is a side of regular hexagon. Find:
(i) ` angle AOB `
(ii) ` angle AOC `
(iii) ` angle AOD `
(iv)` angle BCD`
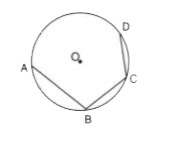
View Solution
CONSTRUCTIONS OF POLYGONS questions and complete solutions for chapter CHAPTER REVISION (STAGE 2) of ICSE of Class 9
All Exercises from SELINA PUBLICATION Class 9 MATHS CHAPTER REVISION (STAGE 2)
- AREA AND PERIMETER OF PLANE FIGURES
- CO- ORDINATE GEOMETRY
- COMPOUND INTEREST
- CONSTRUCTIONS OF POLYGONS
- DISTANCE FORMULA
- FACTRORISATIONS
- GRAPHICAL SOLUTIONS
- INDICES
- INEQUALITIES
- ISOSCELES TRIANGLES
- LOGRITHMS
- MEAN AND MEDIAN
- MID-POINT THEOREM
- RATIONAL AND IRRATIONAL NUMBERS
- RECTILINEAR FIGURES
- SIMULTANEOUS EQUATIONS
- SOLIDS
- STATISTICS
- TRIANGLES
- TRIGONOMETRY