Complete Solutions to MID-POINT THEOREM of chapter CHAPTER REVISION (STAGE 2) of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | CHAPTER REVISION (STAGE 2) |
| SELINA PUBLICATION | MID-POINT THEOREM |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
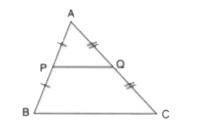
In triangle ABC, P is mid-point of AB and Q is mid-point of AC. If AB = 9.6 cm, BC = 11 cm and AC = 11.2 , find the perimeter of the trapezium PBCQ.
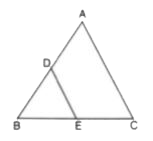
View SolutionIn `Delta ABC, D ` is mid-point of AB and E is
mid -point of BC. Calculate
(i) DE if AC = 6.4 cm,
(ii) ` angle DEB " if " angle ACB = 63^(@) `
View SolutionIn `Delta ABC, D,E ` and F are mid-point of sides AB ,BC and AC respectively , Prove that AE and DF bisect each other.
View SolutionIn a kite shaped figure ABCD , AB = AD and CB = CD , point P,Q and r are mid-point of sides AB,BC and CD respectively . Prove that:
( i) ` angle PQR =90^(@) `
(ii) Line through P and parallel to QR bisects side AD.
View SolutionP,Q,R and S are the mid points of sides AB,BC , CD and DA respectively of rhombus ABCD. Show that PQRS is a rectangle.
Under what conditions will PQRS be a square ?
View SolutionIn a scalene triangle ABC ,AD and BE are medians F is a point in AC so that DF//BE. Show that : AC = 4` xx ` EF.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square, is also a square.
View SolutionABC is an isosceles triangle with AB = AC =13 cm and BC = 10 cm. Calculate the length of the perpendicular from A to BC.
View SolutionIn triangle ABC, AB > AC. E is the mid-point of BC and AD is perpendicular to BC. Prove that : `AB^2 +AC^2=2AE^2 +2BE^2`
View SolutionIn the following figure:
` OA = 2 cm `
` " " = AB = 2BC = (1)/(2) CD = (1)/(6) DE ` Find the length of OE.

View SolutionABC is a triangle in which AB = AC and D is any point on BC. Prove that:
` AB^(2)- AD^(2) = BD. CD `
View SolutionABC is an isosceles triangle with AB = AC = 2a and BC = a . If ` AD bot BC, ` find the length of AD .
View Solution
MID-POINT THEOREM questions and complete solutions for chapter CHAPTER REVISION (STAGE 2) of ICSE of Class 9
All Exercises from SELINA PUBLICATION Class 9 MATHS CHAPTER REVISION (STAGE 2)
- AREA AND PERIMETER OF PLANE FIGURES
- CO- ORDINATE GEOMETRY
- COMPOUND INTEREST
- CONSTRUCTIONS OF POLYGONS
- DISTANCE FORMULA
- FACTRORISATIONS
- GRAPHICAL SOLUTIONS
- INDICES
- INEQUALITIES
- ISOSCELES TRIANGLES
- LOGRITHMS
- MEAN AND MEDIAN
- MID-POINT THEOREM
- RATIONAL AND IRRATIONAL NUMBERS
- RECTILINEAR FIGURES
- SIMULTANEOUS EQUATIONS
- SOLIDS
- STATISTICS
- TRIANGLES
- TRIGONOMETRY