Complete Solutions to EXERCISE 20(A) of chapter AREA AND PERIMETER OF PLANE FIGURES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREA AND PERIMETER OF PLANE FIGURES |
| SELINA PUBLICATION | EXERCISE 20(A) |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
Find the area of a triangle whose sides are 18 cm, 24 cm and 30 cm.
Also, find the length of altitude corresponding to the larger side of the triangle.
View SolutionThe length of the sides of a triangle are in the ratio `3 : 4 : 5`. Find the area of the triangle if its perimeter is 144 cm.
View SolutionABC is a triangle in which AB = AC = 4 cm and `angleA=90^(@)`. Calculate:
the area of `DeltaABC`,
View SolutionABC is a triangle in which AB = AC = 4 cm and `angleA=90^(@)`. Calculate:
the length of perpendicular from A to BC.
View SolutionThe area of an equilateral triangle is `36sqrt(3)` sq. cm. Find its perimeter.
View SolutionFind the area of an isosceles triangle with perimeter 36 cm and base 16 cm.
View SolutionThe base of an isosceles triangle is 24 cm and its area is 192 sq. cm. Find its perimeter.
View SolutionThe given figure shows a right angled triangle ABC and an equilateral triangle BCD.
Find the area of the shaded portion.
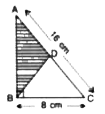
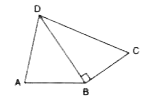
View SolutionFind the area and the perimeter of quadrilateral ABCD, given below, if, AB = 8 cm, AD = 10 cm, BD = 12 cm, DC 13 cm and `angleDBC=90^(@)`.
View SolutionThe base of a triangular field is three times its height. If the cost of cultivating the field at Rs 36.72 per 100 `m^(2)` is Rs 49,572, find its base and height.
View SolutionThe sides of a triangle field are in the ratio `5 : 3 : 4` and its perimeter is 180 m. Find :
its area
View SolutionThe sides of a triangle field are in the ratio `5 : 3 : 4` and its perimeter is 180 m. Find :
altitude of the traingle corresponding to its largest side.
View SolutionThe sides of a triangle field are in the ratio `5 : 3 : 4` and its perimeter is 180 m. Find :
the cost of levelling the field at the rate of Rs 10 per square metre.
View SolutionEach of equal sides of an isosceles triangle is 4 cm greater than its height. If the base of the triangle is 24 cm, calculate the perimeter and the area of the triangle.
View SolutionCalculate the area and the height of an equilateral triangle whose perimeter is 60 cm.
View SolutionIn `DeltaABC`, angle `A=90^(@)`, side AB = x cm, AC = `(x+5)` cm and area = 150 `cm^(2)`. Find the sides of triangle.
View SolutionIf the difference between the sides of a right angled triangle is 3 cm and its area is 54 `cm^(2)`, find its perimeter.
View SolutionAD is altitude of an isosceles triangle ABC in which AB = AC = 30 cm and BC = 36 cm. A point O is marked on AD in such a way that `angleBOC=90^(@)`. Find the area of quadrilateral ABOC.
View Solution
EXERCISE 20(A) questions and complete solutions for chapter AREA AND PERIMETER OF PLANE FIGURES of ICSE of Class 9