Complete Solutions to Question of chapter AREA AND PERIMETER OF PLANE FIGURES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREA AND PERIMETER OF PLANE FIGURES |
| SELINA PUBLICATION | Question |
| Number Of Questions | 33 |
| Academic Year | 2023-24 |
Find the area of a triangle :
whose height is 6 cm and base is 10 cm.
View SolutionFind the area of a triangle :
whose three sides are 17 cm, 8 cm and 15 cm long.
Also, in part (ii) of the question, calculate the length of the altitude corresponding to the largest side of the triangle.
View SolutionThe area of an equilateral triangle is numerically equal to its perimeter.
Find a side of the triangle [Take `sqrt(3)=1.73`].
View SolutionCalculate the area of an equilateral triangle, whose height is 20 cm.
View SolutionFind the area of an isosceles triangle whose equal sides are 5 cm each and base is 6 cm.
View SolutionThe sides of a triangle containing the right angle are 5x cm and `(3x-1)` cm. If the area of the triangle is 60 `cm^(2)`, calculate the lengths of the sides of the triangle.
View SolutionThe given figure shows an equilateral triangle ABC whose each side is 10 cm and a right-angled triangle BDC whose side BD = 8 cm and `angleD=90^(@)`. Find the area of the shaded portion.
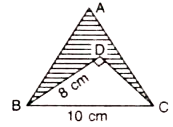
View SolutionA kite is made as shown alongside in which ABC is an equilateral triangle with side 20 cm, BOC is an isosceles triangle with OB = OC = 26 cm and ODE is an isosceles triangle with base DE = 8 cm and height 6 cm. Find the whole area of the kite.

View SolutionThe area of an isosceles triangle is `60c m^2` and the length of each one of its equal sides is 13 cm. Find its base.
View SolutionThe perimeter of a rectangle is 25.5 m. Its length is 9.5 m. Calculate its area in sq. m `(m^(2))`.
View SolutionA room is 8 m long and 5 m broad. Find the cost of covering the floor of the room with 80 cm wide carpet at the rate of Rs 225 per metre.
View SolutionThe area of a square field is 484 `m^(2)`. Find :
the length of its one side,
View SolutionThe area of a square field is 484 `m^(2)`. Find :
the length of its diagonal, correct to two places of decimal.
View SolutionTwo adjacent sides of a parallelogram are 15 cm and 10 cm. If the distance between 15 cm sides is 8 cm, find the distance between 10 cm sides.
View SolutionPQRS is a rhombus.
If it is given that PQ = 3 cm, calculate the perimeter of PQRS.
View SolutionPQRS is a rhombus.
If it is given that PQ=3cm and if the height of the rhombus is 2.5 cm, calculate the area.
View SolutionThe given figure shows a trapezium ABCD in which AB = 17 cm, BC = 8 cm and CD = 15 cm. Find the area and perimeter of the trapezium.
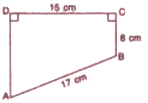
View SolutionFind the area of the trapezium whose parallel sides are 15 cm amd 23 cm, whereas the non-parallel sides are 10 cm and 8 cm.
View SolutionA footpath of uniform width runs all around the inside of a rectangular field 38 m long and 32 m wide. If the path occupies 600 `m^(2)`, find its width.
View SolutionA wire is bent in the form of an equilateral triangle of largest area. If it encloses an area of `49sqrt(3)` `cm^(2)`, find the largest area enclosed by the same wire when bent to form :
a square
View SolutionA wire is bent in the form of an equilateral triangle of largest area. If it encloses an area of `49sqrt(3)` `cm^(2)`, find the largest area enclosed by the same wire when bent to form :
a rectangle of length 12 cm.
View SolutionThe distance between parallel sides of a trapezium is 20 cm and the length of the line segment joining the mid-points of its non-parallel sides is 53 cm. Find the area of the trapezium.
View SolutionArea of a square is same as that of a rectangle. The length and the breadth of the rectangle are respectively 5 cm more and 4 cm less than the side of the square. Find the side of the square.
View SolutionThe circumference of a circle exceeds its diameter by 270 cm. Find its diameter.
View SolutionFind the diameter of the circle whose circumference is equal to the sum of the circumference of circles with radii 5 cm, 8 cm and 10 cm.
View SolutionThe area of a circle is numerically equal to its circumference. Find its area (Take `pi=3.14`).
View SolutionA rectangular sheet of paper is 35 cm long and 28 cm wide. Find the area of the largest circle that can be cut from this sheet.
View SolutionFind the perimeter of a cirlce whose area is equal to sum of areas of the circles with diameters 10 cm and 24 cm. Give your answer correct to two decimal places.
View SolutionThe radii of two circles are in the ratio `5 : 8`. If the difference between their areas is 351`pi` sq. cm, find the area of the bigger circle. Take `pi=3.14`.
View SolutionA uniform circular track is the area bounded by two concentric circles. If the ares of the track is 1144 `m^(2)` and its width is 14 m, find the diameters of the two circles.
View SolutionThe radii of the wheel of a car is 28 cm. Find the number of rotations made by the wheel in order to cover a distance of 4.4 km ?
View SolutionA circular wheel if radius 28 cm makes 300 revolutions per minute. Find the speed of the wheel in kilometre per hour.
View SolutionIn the given figure, find the area of the unshaded portion within the rectangle. (Take `pi=3.14`).

View Solution
Question questions and complete solutions for chapter AREA AND PERIMETER OF PLANE FIGURES of ICSE of Class 9