Complete Solutions to EXAMPLE of chapter TRIGONOMETRICAL RATIOS OF STANDARD ANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIGONOMETRICAL RATIOS OF STANDARD ANGLES |
| SELINA PUBLICATION | EXAMPLE |
| Number Of Questions | 48 |
| Academic Year | 2023-24 |
Evaluate :
(i) `sin^(2)30^(@)-2cos^(3)60^(@)+3tan^(4)45^(@)`
(ii) `(cos0^(@)+sin45^(@)+sin30^(@))(sin90^(@)-cos45^(@)+cos60^(@))`
View SolutionFind the value of :
` (sin30^(@)-sin90^(@)+2cos0^(@))/(tan30^(@) times tan60^(@))`
View SolutionIf `A=60^(@)`, verify that :
(i) `sin^(2)A+cos^(2)A=1" (ii) "sec^(2)A-tan^(2)A=1`
View SolutionIf `x=15^(@)`, evaluate : `8sin2xcos4xsin6x`
View SolutionIf `A=60^(@) and B=30^(@)`, prove that :
`" "sin(A-B)=sinAcosB-cosAsinB`
View SolutionIf `A=30^(@)`, then prove that :
`" "cos3A=4cos^(3)A-3cosA`
View SolutionFind A, if :
`sin2A=1`
View SolutionFind A, if :
`2cos3A=1`
View SolutionFind A, if :
`(secA-2)(tan3A-1)=0`
View SolutionFrom the adjoining figure, find : `tanx^(@)`
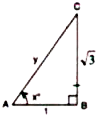
View SolutionFrom the adjoining figure, find :
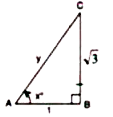
`x^(@)`
View SolutionFrom the adjoining figure, find : `cosx^(@)`
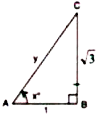
View SolutionFrom the adjoining figure, find :

use `tanx^(@)` to find y.
View SolutionIf `4sin^(2)x^(@)-3=0" and "x^(@)` is an acute angle, find :
(i) `sinx^(@) " (ii) "x^(@)`
View SolutionFind the magnitude of angle A, if :
`4sinAsin2A+1-2sin2A=2sinA`
View SolutionFind the magnitude of angle A, if :
`2sin^(2)A-3sinA+1=0`
View SolutionFind the magnitude of angle A, if :
`3cot^(2)(A-5^(@))=1`
View SolutionFind the magnitude of angle A, if :
`sin^(2)2A+sin^(2)60^(@)=1`
View SolutionFind acute angles A and B, if `sin(A+B)=cos(A-B)=sqrt(3)/2`.
View SolutionIf `tan(A+B)=sqrt(3) and sqrt(3)tan(A-B)=1`, find the angles A and B,where A and B are Acute Angles.
View SolutionIf `sqrt(3)tan2theta=3 and 0^(@) lt theta le 90^(@)`, find the value of `3sqrt(3)costheta+2sintheta-6tan^(2)theta`.
View SolutionSolve for `theta(0^(@) lt theta lt 90^(@))` :
`sin^(2)theta-1/2sintheta=0`
View SolutionSolve for `theta(0^(@) lt theta lt 90^(@))` :
`2sin^(2)theta-2costheta=1/2`
View SolutionSolve for `theta(0^(@) lt theta lt 90^(@))` :
`tan^(2)theta+3=3sectheta`.
View SolutionEvaluate :
(i) `sin^(2)30^(@)-2cos^(3)60^(@)+3tan^(4)45^(@)`
(ii) `(cos0^(@)+sin45^(@)+sin30^(@))(sin90^(@)-cos45^(@)+cos60^(@))`
View SolutionFind the value of :
`" "(sin30^(@)-sin90^(@)+2cos0^(@))/(tan30^(@) times tan60^(@))`
View SolutionIf `A=60^(@)`, verify that :
(i) `sin^(2)A+cos^(2)A=1" (ii) "sec^(2)A-tan^(2)A=1`
View SolutionIf `x=15^(@)`, evaluate : `8sin2xcos4xsin6x`
View SolutionIf `A=60^(@) and B=30^(@)`, prove that :
`" "sin(A-B)=sinAcosB-cosAsinB`
View SolutionIf `A=30^(@)`, then prove that :
`" "cos3A=4cos^(3)A-3cosA`
View SolutionFind A, if :
`sin2A=1`
View SolutionFind A, if :
`2cos3A=1`
View SolutionFind A, if :
`(secA-2)(tan3A-1)=0`
View SolutionFrom the adjoining figure, find :

`tanx^(@)`
View SolutionFrom the adjoining figure, find :

`x^(@)`
View SolutionFrom the adjoining figure, find :

`cosx^(@)`
View SolutionFrom the adjoining figure, find :

use `sinx^(@)` to find y.
View SolutionIf `4sin^(2)x^(@)-3=0" and "x^(@)` is an acute angle, find :
(i) `sinx^(@) " (ii) "x^(@)`
View SolutionFind the magnitude of angle A, if :
`4sinAsin2A+1-2sin2A=2sinA`
View SolutionFind the magnitude of angle A, if :
`2sin^(2)A-3sinA+1=0`
View SolutionFind the magnitude of angle A, if :
`3cot^(2)(A-5^(@))=1`
View SolutionFind the magnitude of angle A, if :
`sin^(2)2x+sin^(2)60^(@)=1`
View SolutionFind acute angles A and B, if `sin(A+B)=cos(A-B)=sqrt(3)/2`.
View SolutionIf `tan(A+B)=sqrt(3) and sqrt(3)tan(A-B)=1`, find the angles A and B.
View SolutionIf `sqrt(3)tan2theta=3 and 0^(@) lt theta le 90^(@)`, find the value of `3sqrt(3)costheta+2sintheta-6tan^(2)theta`.
View SolutionSolve for `theta(0^(@) lt theta lt 90^(@))` :
`sin^(2)theta-1/2sintheta=0`
View SolutionSolve for `theta(0^(@) lt theta lt 90^(@))` :
`2sin^(2)theta-2costheta=1/2`
View SolutionSolve for `theta(0^(@) lt theta lt 90^(@))` :
`tan^(2)theta+3=3sectheta`.
View Solution
EXAMPLE questions and complete solutions for chapter TRIGONOMETRICAL RATIOS OF STANDARD ANGLES of ICSE of Class 9