Complete Solutions to EXERCISE 23(C) of chapter TRIGONOMETRICAL RATIOS OF STANDARD ANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIGONOMETRICAL RATIOS OF STANDARD ANGLES |
| SELINA PUBLICATION | EXERCISE 23(C) |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Solve the following equations for A, if :
`2sinA=1`
View SolutionSolve the following equations for A, if :
`2cos2A=1`
View SolutionSolve the following equations for A, if :
`sin3A=sqrt(3)/2`
View SolutionSolve the following equations for A, if :
`sec2A=2`
View SolutionSolve the following equations for A, if :
`sqrt(3)tanA=1`
View SolutionSolve the following equations for A, if :
`tan3A=1`
View SolutionSolve the following equations for A, if :
`2sin3A=1`
View SolutionSolve the following equations for A, if :
`sqrt(3)cot2A=1`
View SolutionCalculate the value of A, if :
`(sinA-1)(2cosA-1)=0`
View SolutionCalculate the value of A, if :
`(tanA-1)(cosec3A-1)=0`
View SolutionCalculate the value of A, if :
`(sec2A-1)(cosec3A-1)=0`
View SolutionCalculate the value of A, if :
`cos3A.(2sin2A-1)=0`
View SolutionCalculate the value of A, if :
`(cosec2A-2)(cot3A-1)=0`
View SolutionIf `2sinx^(@)-1=0 and x^(@)` is an acute angle, find:
(i) b`sinx^(@)" (ii) "x^(@)" (iii) "cosx^(@) and tanx^(@)`.
View SolutionIf `4cos^(2)x^(@)-1=0 and 0 le x^(@) le 90^(@)`, find :
`x^(@)`
View SolutionIf `4cos^(2)x^(@)-1=0 and 0 le x^(@) le 90^(@)`, find :
`sin^(2)x^(@)+cos^(2)x^(@)`
View SolutionIf `4cos^(2)x^(@)-1=0 and 0 le x^(@) le 90^(@)`, find :
`1/(cos^(2)x^(@))-tan^(2)x^(@)`
View SolutionIf `4sin^(2)theta-1=0` and angle `theta` is less than `90^(@)`, find the value of `theta` and hence the value of `cos^(2)theta+tan^(2)theta`.
View SolutionIf `sin3A=1 and 0 le A le 90^(@)`, find :
sin A
View SolutionIf `sin3A=1 and 0 le A le 90^(@)`, find :
`cos 2A`
View SolutionIf `sin3A=1 and 0 le A le 90^(@)`, find :
`tan^(2)A-1/(cos^(2)A)`
View SolutionIf `2cos2A=sqrt(3)` and A is acute, find :
A
View SolutionIf `2cos2A=sqrt(3)` and A is acute, find :
sin 3A
View SolutionIf `2cos2A=sqrt(3)` and A is acute, find :
`sin^(2)(75^(@)-A)+cos^(2)(45^(@)+A)`
View SolutionIf `sinx+cosy=1" and "x=30^(@)`, find the value of y.
View SolutionIf `3tanA-5cosB=sqrt(3) and B=90^(@)`, find the value of A.
View SolutionFrom the given figure, find :
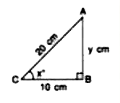
`cosx^(@)`
View SolutionFrom the given figure, find :
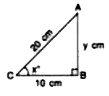
`x^(@)`
View SolutionFrom the given figure, find :
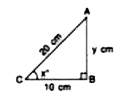
`1/(tan^(2)x^(@))-1/(sin^(2)x^(@))`
View SolutionFrom the given figure, find :
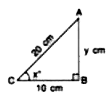
Use `tanx^(@)`, to find the value of y.
View SolutionUse the given figure to find :
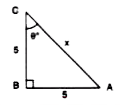
`tantheta^(@)`
View SolutionUse the given figure to find :
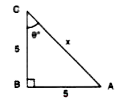
`theta^(@)`
View SolutionUse the given figure to find :
`sin^(2)theta^(@)-cos^(2)theta^(@)`
View SolutionUse the given figure to find :

`theta^(@)`
View SolutionFind the magnitude of angle A, if :
`2sinAcosA-cosA-2sinA+1=0`
View SolutionFind the magnitude of angle A, if :
`tanA-2cosAtanA+2cosA-1=0`
View SolutionFind the magnitude of angle A, if :
`2cos^(2)A-3cosA+1=0`
View SolutionFind the magnitude of angle A, if :
`2tan3Acos3A-tan3A+1=2cos3A`
View SolutionSolve for x :
`2cos3x-1=0`
View SolutionSolve for x :
`cos""x/3-1=0`
View SolutionSolve for x :
`sin(x+10^(@))=1/2`
View SolutionSolve for x :
`cos(2x-30^(@))=0`
View SolutionSolve for x :
`2cos(3x-15^(@))=1`
View SolutionSolve for x :
`tan^(2)(x-5^(@))=3`
View SolutionSolve for x :
`3tan^(2)(2x-20^(@))=1`
View SolutionSolve for x :
`cos(x/2+10^(@))=sqrt(3)/2`
View SolutionSolve for x :
`sin^(2)x+sin^(2)30^(@)=1`
View SolutionSolve for x :
`cos^(2)30^(@)+cos^(2)x=1`
View SolutionSolve for x :
`cos^(2)30^(@)+sin^(2)2x=1`
View SolutionSolve for x :
`sin^(2)60^(@)+cos^(2)(3x-9^(@))=1`
View SolutionIf `4cos^(2)x=3 and x` is an acute angle, find the value of :
x
View SolutionIf `4cos^(2)x=3 and x` is an acute angle, find the value of :
`cos^(2)x+cot^(2)x`
View SolutionIf `4cos^(2)x=3 and x` is an acute angle, find the value of :
`cos3x`
View SolutionIf `4cos^(2)x=3 and x` is an acute angle, find the value of :
`sin2x`
View SolutionIn `DeltaABC, angleB=90^@), AB=y" units", BC=sqrt(3) " units"`, AC = 2 units and angle `A=x^(@)`, find :
`sinx^(@)`
View SolutionIn `DeltaABC, angleB=90^@), AB=y" units", BC=sqrt(3) " units"`, AC = 2 units and angle `A=x^(@)`, find :
`x^(@)`
View SolutionIn `DeltaABC, angleB=90^@), AB=y" units", BC=sqrt(3) " units"`, AC = 2 units and angle `A=x^(@)`, find :
`tanx^(@)`
View SolutionIn `DeltaABC, angleB=90^@), AB=y" units", BC=sqrt(3) " units"`, AC = 2 units and angle `A=x^(@)`, find :
use `cosx^(@)` to find the value of y.
View SolutionIf `2cos(A+B)=2sin(A-B)=1`, find the values of A and B.
View SolutionSolve the following equations for A, if :
`2sinA=1`
View SolutionSolve the following equations for A, if :
`2cos2A=1`
View SolutionSolve the following equations for A, if :
`sin3A=sqrt(3)/2`
View SolutionSolve the following equations for A, if :
`sec2A=2`
View SolutionSolve the following equations for A, if :
`sqrt(3)tanA=1`
View SolutionSolve the following equations for A, if :
`tan3A=1`
View SolutionSolve the following equations for A, if :
`2sin3A=1`
View SolutionSolve the following equations for A, if :
`sqrt(3)cot2A=1`
View SolutionCalculate the value of A, if :
`(sinA-1)(2cosA-1)=0`
View SolutionCalculate the value of A, if :
`(tanA-1)(cosec3A-1)=0`
View SolutionCalculate the value of A, if :
`(sec2A-1)(cosec3A-1)=0`
View SolutionCalculate the value of A, if :
`cos3A.(2sin2A-1)=0`
View SolutionCalculate the value of A, if :
`(cosec2A-2)(cot3A-1)=0`
View SolutionIf `2sinx^(@)-1=0 and x^(@)` is an acute angle, find:
(i) b`sinx^(@)" (ii) "x^(@)" (iii) "cosx^(@) and tanx^(@)`.
View SolutionIf `4cos^(2)x^(@)-1=0 and 0 le x^(@) le 90^(@)`, find :
`x^(@)`
View SolutionIf `4cos^(2)x(@)-1=0 and 0 le x^(@) le 90^(@)`, find :
`sin^(2)x^(@)+cos^(2)x^(@)`
View SolutionIf `4cos^(2)x(@)-1=0 and 0 le x^(@) le 90^(@)`, find :
`1/(cos^(2)x^(@))-tan^(2)x^(@)`
View SolutionIf `4sin^(2)theta-1=0` and angle `theta` is less than `90^(@)`, find the value of `theta` and hence the value of `cos^(2)theta+tan^(2)theta`.
View SolutionIf `sin3A=1 and 0 le A le 90^(@)`, find :
sin A
View SolutionIf `sin3A=1 and 0 le A le 90^(@)`, find :
`cos 2A`
View SolutionIf `sin3A=1 and 0 le A le 90^(@)`, find :
`tan^(2)A-1/(cos^(2)A)`
View SolutionIf `2cos2A=sqrt(3)` and A is acute, find :
A
View SolutionIf `2cos2A=sqrt(3)` and A is acute, find :
sin 3A
View SolutionIf `2cos2A=sqrt(3)` and A is acute, find :
`sin^(2)(75^(@)-A)+cos^(2)(45^(@)+A)`
View SolutionIf `sinx+cosy=1" and "x=30^(@)`, find the value of y.
View SolutionIf `3tanA-5cosB=sqrt(3) and B=90^(@)`, find the value of A.
View SolutionFrom the given figure, find :

`cosx^(@)`
View SolutionFrom the given figure, find :

`x^(@)`
View SolutionFrom the given figure, find :

`1/(tan^(2)x^(@))-1/(sin^(2)x^(@))`
View SolutionFrom the given figure, find :

Use `tanx^(@)`, to find the value of y.
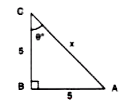
View SolutionUse the given figure to find :

`tantheta^(@)`
View SolutionUse the given figure to find :

`theta^(@)`
View SolutionUse the given figure to find :

`sin^(2)theta^(@)-cos^(2)theta^(@)`
View SolutionUse the given figure to find :
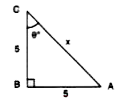
Use `sintheta^(@)` to find the value of x.
View SolutionFind the magnitude of angle A, if :
`2sinAcosA-cosA-2sinA+1=0`
View SolutionFind the magnitude of angle A, if :
`tanA-2cosAtanA+2cosA-1=0`
View SolutionFind the magnitude of angle A, if :
`2cos^(2)A-3cosA+1=0`
View SolutionFind the magnitude of angle A, if :
`2tan3Acos3A-tan3A+1=2cos3A`
View SolutionSolve for x :
`2cos3x-1=0`
View SolutionSolve for x :
`cos""x/3-1=0`
View SolutionSolve for x :
`sin(x+10^(@))=1/2`
View Solution
EXERCISE 23(C) questions and complete solutions for chapter TRIGONOMETRICAL RATIOS OF STANDARD ANGLES of ICSE of Class 9