Complete Solutions to EXAMPLES of chapter UPTHRUST IN FLUIDS, ARCHIMEDES' PRINCIPLE AND FLOATATION of Class 9 book with complete answers and questions
| Class 9 | PHYSICS |
| Chapter | UPTHRUST IN FLUIDS, ARCHIMEDES' PRINCIPLE AND FLOATATION |
| SELINA PUBLICATION | EXAMPLES |
| Number Of Questions | 17 |
| Academic Year | 2023-24 |
A body weighs 200 gf in air and 190 gf when completely immersed in water. Calculate:
(i) the loss in weight of the body in water.
(ii) the upthrust on the body.
View SolutionA small stone of mass m(=200g) is held under water in a jar and is allowed to fall as shown in fig. the forces acting on stone are also shown.
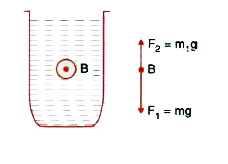
(i) What does `F_(2)` represent ?
(ii) What does `m_(1)` represent?
(iii) What is the net force acting on stone?
(iv) What is the acceleration of stone as it falls through water? Neglect the force due to viscosity. Assume that the volume of stone
`=80cm^(3)`, density of water `=1.0gcm^(-3)` and acceleration due to gravity `g=10ms^(-2)`
View SolutionA piece of iron of density `7.8xx10^(3)kgm^(-3)` and volume `100cm^(3)` is completely immersed in water `(rho=1000kgm^(-3))`. Calculate (i) the weight of iron piece in air (ii) the upthrust and (iii) its apparent weight in water . `(g=10ms^(-2))`
View SolutionA metal cube of side 5 cm and density `7.9gcm^(-3)` is suspended by a thread and is immersed completely in a liquid of density `1.1gcm^(-3)`, Find (a) the weight of cube (b) the upthrust on cube and (c) the tension in thread. (Take g=10ms−2)
View SolutionA solid of density `rho` has weight W. Show that its apparent weight will be `W[1-(rho_(L)//rho)]` when it is completely immersed in a liquid of densilty `rho_(L)`.
View SolutionRelative density of silver is 10.5. What is the density of silver in S.I. unit? What assumption do you make in your calculations.
View SolutionA Solid weighs 50 gf in air and 44 gf when completely immersed in water. Calculate:
(i) the upthrust,
(ii) the volume of the solid, and
(iii) the relative density of the solid.
View SolutionA solid weighs 30 gf in air and 26 gf when completely immersed in a liquid of relative density 0.8. Find : (i) the volume of solid, and (ii) the relative density of solid.
View SolutionA solid body weighs 2.10 N in air. Its relative density is 8.4. How much will the body weigh if placed
(i) in water
(ii) in a liquid of relative density `1.2`?
View SolutionA body weighs 82.1 gf in air, 75.5 gf in water and 73.8 gf in a liquid. A. Find the relative density of the liquid. B. How much will it weigh if immersed in a liquid of relative density 0.87 ?
View SolutionA block of wood of volume `25cm^(3)` floats on water with `20cm^(3)` of its volume immersed. Calculate (i) the density, and (ii) the weight of block of wood.
View SolutionA block of iron floats on mercury. Find the fractionof volume which remains immersed in mercury. (Densities of iron and mercury are `7.8gcm^(-3)` and `13.6gcm^(-3)` respectively).
View SolutionAn iceberg floats on fresh water with a part of it outside the water surface. Calculate the fraction of the volume of the iceberg which is below the water surface.
Given : density of ice `=917kgm^(-3)`, density of fresh water `=1000kgm^(-3)`
View SolutionA block of wood floats on water with `2/5` th of its volume above the water surface. Calculate the density of wood.
View SolutionA piece of wood of volume `200cm^(3)` and density `0.84gcm^(-3)` floats in a liquid of density `1.05gcm^(-3)`
(i) What volume of wood will remain above the surface of liquid?
(ii) What force must be exerted on wood to keep it totally submerged?
View SolutionThe volume of a balloon is `1000m^(3)`. It is filled with helium of density `0.18kgm^(-3)`. What maximum load can it life. Density of air is `1.29kgm^(-3)`
View SolutionTwo identical blocks A and b of different materials float on water such that 90% of A and 15% of B remain submerged inside water. Compare:
(i) density of A and B.
View Solution
EXAMPLES questions and complete solutions for chapter UPTHRUST IN FLUIDS, ARCHIMEDES' PRINCIPLE AND FLOATATION of ICSE of Class 9