A block of wood floats on water with 25 th of its volume above the water surface. Calculate the density of wood.
To solve the problem of finding the density of wood, we can follow these steps:
1. Understand the Problem: We have a block of wood floating on water, with 25 of its volume above the water surface. We need to find the density of the wood.
2. Define Variables:
- Let the total volume of the wooden block be V.
- The volume of the block above the water surface is given as 25V.
- Therefore, the volume of the block submerged in water (emerged volume) is:
Vsubmerged=V−25V=35V
3. Apply Archimedes' Principle: According to Archimedes' principle, the weight of the water displaced by the submerged part of the block is equal to the weight of the block itself.
- The weight of the block can be expressed as:
Weight of block=Density of wood×Volume of wood×g=ρ×V×g
- The weight of the water displaced is:
Weight of displaced water=Density of water×Volume of water displaced×g=1×(35V)×g
(Here, we take the density of water as 1g/cm3 for simplicity.)
4. Set Up the Equation: According to Archimedes' principle:
Weight of block=Weight of displaced water
Therefore:
ρ×V×g=1×(35V)×g
5. Cancel Common Terms: Since g and V are on both sides of the equation, we can cancel them out:
ρ=35
6. Convert to Appropriate Units: The density of wood is:
ρ=0.6g/cm3
Final Answer:
The density of the wood is 0.6g/cm3.
- Let the total volume of the wooden block be V.
- The volume of the block above the water surface is given as 25V.
- Therefore, the volume of the block submerged in water (emerged volume) is:
Vsubmerged=V−25V=35V
Weight of block=Density of wood×Volume of wood×g=ρ×V×g
- The weight of the water displaced is:
Weight of displaced water=Density of water×Volume of water displaced×g=1×(35V)×g
(Here, we take the density of water as 1g/cm3 for simplicity.)
Weight of block=Weight of displaced water
Therefore:
ρ×V×g=1×(35V)×g
ρ=35
ρ=0.6g/cm3
The density of the wood is 0.6g/cm3.
Topper's Solved these Questions
- UPTHRUST IN FLUIDS, ARCHIMEDES' PRINCIPLE AND FLOATATIONBOOK - ICSECHAPTER - UPTHRUST IN FLUIDS, ARCHIMEDES' PRINCIPLE AND FLOATATIONEXERCISE - EXERCISE 5(A)
28 Videos
- UPTHRUST IN FLUIDS, ARCHIMEDES' PRINCIPLE AND FLOATATIONBOOK - ICSECHAPTER - UPTHRUST IN FLUIDS, ARCHIMEDES' PRINCIPLE AND FLOATATIONEXERCISE - EXERCISE 5(A) (Multiple Choice Question)
3 Videos
- SOUNDBOOK - ICSECHAPTER - SOUNDEXERCISE - TOPIC 2 Infrasonic and Ultrasonic Waves ( 3 Marks Questions)
3 Videos
Similar Questions
A wooden block floats in water with two third of its volume submerged. A. Calculate the density of wood.b. When the same block is placed in oil, three - quarter of its volume in immersed in oil. Calculate the density of oil.
View SolutionThe densit of a block of wood which flots on water with 0.1 of its volume above water is:
View Solution
Knowledge Check
A block of wood floats in water with (4/5)th of its volume submerged. If the same block just floats in a liquid, the density of liquid in (kgm−3) is
A1250B600C400D800
A block of wood of volume 30cm3 floats it water with 20cm3 of its volume immersed.
Calculate the density.
View SolutionA block of wood of volume 30cm3 floats in water with 20cm3 of its volume immersed.
Calculate the weight of the block of wood .
View SolutionA block of wood of volume 25cm3 floats on water with 20cm3 of its volume immersed. Calculate (i) the density, and (ii) the weight of block of wood.
View SolutionAn ice berg floats on fresh water with a part of it outside the water surface. Calculate the fraction of the volume of the ice berg which is below the water surface. (Density of ice = 917kgm−3, Density of water = 1000kgm−3 )
View SolutionA block of wood floats in water with (4/5)th of its volume submerged. If the same block just floats in a liquid, the density of liquid in (kgm−3) is
View Solution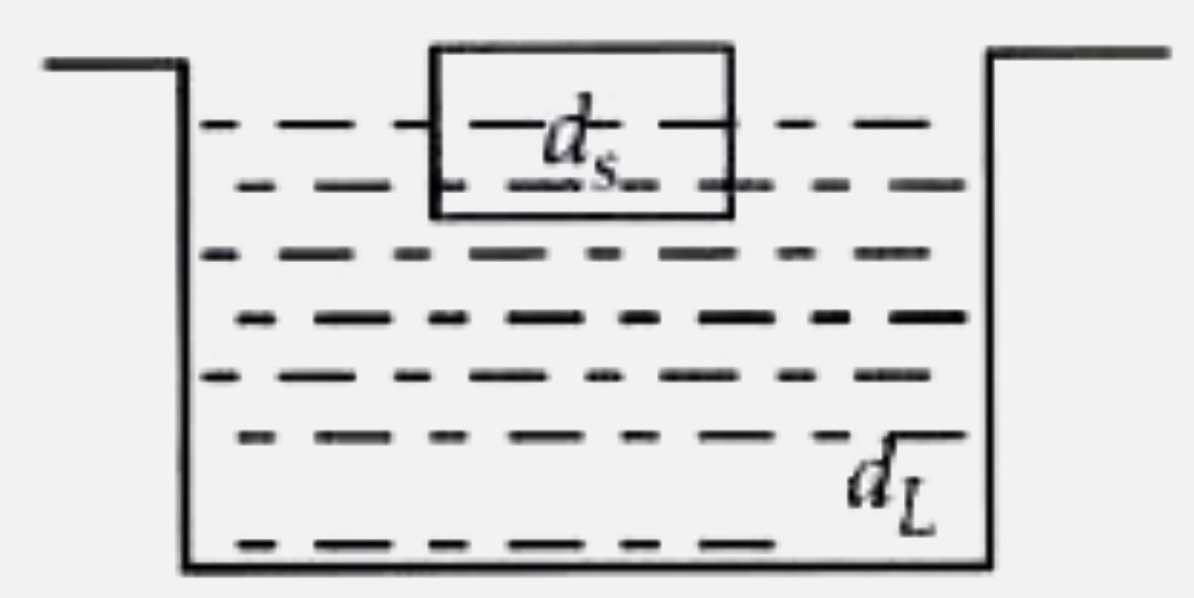
The figure above shows a solid of density dS floating in a liquid of density dL.
The same solid floats in water with 3th5 of its volume immersed in it. Calculate the density of the solid. (density of water = 1 g cm−3 )
View SolutionAn iceberg floats on fresh water with a part of it outside the water surface. Calculate the fraction of the volume of the iceberg which is below the water surface.
Given : density of ice =917kgm−3, density of fresh water =1000kgm−3
View Solution
