Complete Solutions to Exercise of chapter Lines and Angles of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | Lines and Angles |
| MBD | Exercise |
| Number Of Questions | 95 |
| Academic Year | 2023-24 |
In Fig.
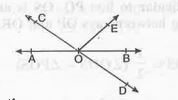 , lines AB and CD intersect at O. If `angleAOC+angleBOE=70^@` and `angleBOD = 40^@`, find `angleBOE` and reflex `angleCOE`.
, lines AB and CD intersect at O. If `angleAOC+angleBOE=70^@` and `angleBOD = 40^@`, find `angleBOE` and reflex `angleCOE`.
View SolutionIn Fig.
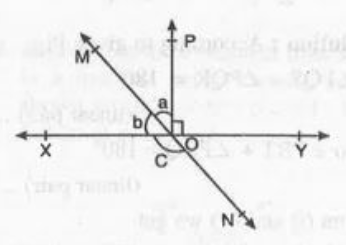
lines XY and MN intersect at O. If `anglePOY = 90^@` and `a : b = 2 : 3`, find C.
View SolutionIn given fig.
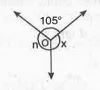 if `n - x = 3^@` find x and n.
if `n - x = 3^@` find x and n.
View SolutionIn fig.
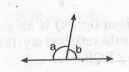
if `a` is greater than `b` by one third of right angle. Find the values of `a` and `b`.
View SolutionIf ray OC stands on line AB such that `angleAOC = angleBOC` (see fig.
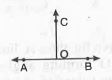 ) show that `angleAOC = 90^@`.
) show that `angleAOC = 90^@`.
View SolutionIn given fig.

Rays OA, OB, OC, OD and OE have common initial point O. Show that `angleAOB + angleBOC + angleCOD + angleDOE + angleEOA = 360^@`.
View SolutionIn the given Fig
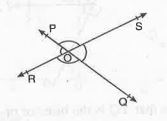 , lines, PQ and RS intersect each other at point O. If `anglePOR ∶ angleROQ = 5 : 7`, find the measure of all angles.
, lines, PQ and RS intersect each other at point O. If `anglePOR ∶ angleROQ = 5 : 7`, find the measure of all angles.
View SolutionIn the given fig.
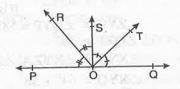 , ray OS is on POQ. Rays OR and OT are the bisectors of `anglePOS` and `angleSOQ` respectively. If `anglePOS = x` find `angleROT` .
, ray OS is on POQ. Rays OR and OT are the bisectors of `anglePOS` and `angleSOQ` respectively. If `anglePOS = x` find `angleROT` .
View SolutionIn fig.
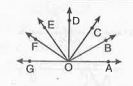 `angleAOF` and `angleFOG` form linear pair. `angleEOB = angle FOC = 90° and `angleDOC = `angleFOG` = `angleAOB` = 30^@`. `
Find the measure of `angleFOE`, `angleCOB` and `angleDOE`.
`angleAOF` and `angleFOG` form linear pair. `angleEOB = angle FOC = 90° and `angleDOC = `angleFOG` = `angleAOB` = 30^@`. `
Find the measure of `angleFOE`, `angleCOB` and `angleDOE`.
View SolutionMatch the following :
 .
.
View SolutionIn fig.
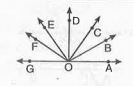 `angleAOF` and `angleFOG` form linear pair. `angleEOB = angle FOC = 90° and `angleDOC = angleFOG = angleAOB = 30^@`.Name three pairs of adjacent complementary angles.
`angleAOF` and `angleFOG` form linear pair. `angleEOB = angle FOC = 90° and `angleDOC = angleFOG = angleAOB = 30^@`.Name three pairs of adjacent complementary angles.
View SolutionIn fig.
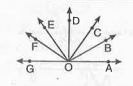 `angleAOF` and `angleFOG` form linear pair. `angleEOB = angle FOC = 90° and `angleDOC = angleFOG = angleAOB = 30^@`.Name three pairs of complementary angles other than those covered in adjacent complementary angles.
`angleAOF` and `angleFOG` form linear pair. `angleEOB = angle FOC = 90° and `angleDOC = angleFOG = angleAOB = 30^@`.Name three pairs of complementary angles other than those covered in adjacent complementary angles.
View SolutionIn fig.
 `angleAOF` and `angleFOG` form linear pair. `angleEOB = angle FOC = 90° and `angleDOC = angleFOG = angleAOB = 30^@`.Name three pairs of adjacent complementary angles.
`angleAOF` and `angleFOG` form linear pair. `angleEOB = angle FOC = 90° and `angleDOC = angleFOG = angleAOB = 30^@`.Name three pairs of adjacent complementary angles.
View SolutionIn fig.
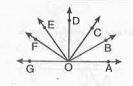 `angleAOF` and `angleFOG` form linear pair. `angleEOB = angle FOC = 90° and `angleDOC = angleFOG = angleAOB = 30^@`.Name three pairs of supplementary angle.
`angleAOF` and `angleFOG` form linear pair. `angleEOB = angle FOC = 90° and `angleDOC = angleFOG = angleAOB = 30^@`.Name three pairs of supplementary angle.
View SolutionIn fig.
 `angleAOF` and `angleFOG` form linear pair. `angleEOB = angle FOC = 90° and `angleDOC = angleFOG = angleAOB = 30^@`.Name three pairs of complementary angles other than those covered in adjacent complementary angles.
`angleAOF` and `angleFOG` form linear pair. `angleEOB = angle FOC = 90° and `angleDOC = angleFOG = angleAOB = 30^@`.Name three pairs of complementary angles other than those covered in adjacent complementary angles.
View SolutionIn given fig.
 AB and CD are two intersecting lines. OP and OQ are respectively bisectors of `/_BOD` and `/_AOC` . Show that OP and OQ are opposite rays.
AB and CD are two intersecting lines. OP and OQ are respectively bisectors of `/_BOD` and `/_AOC` . Show that OP and OQ are opposite rays.
View SolutionAngles forming a linear pair are supplementary.
View SolutionIf two adjacent angles are equal, then each angle measures `90^@`.
View SolutionAngles forming a linear pair can both the acute angles.
View SolutionTwo distinct lines in a plane can have two points in common.
View SolutionIf angles forming a linear pair are equal, then each of these angles is of measure `90^@`.
View SolutionIf two lines intersect and if one pair of vertically opposite angles is formed by acute angles, then the other pair of vertically opposite angles will be formed by obtuse angles.
View SolutionIf two lines intersect and one of the angles so formed is a right angle, then the other three angles will not be right angles.
View SolutionTwo distinct points in a plane determine a ............ Line.
View SolutionTwo distinct .......... in a plane cannot have more than one point in common.
View SolutionGiven a line and a point, not on the line, there is one and only ........... line which passes through the given point and is to the given line.
View SolutionA line separates a plane into ............ parts namely the two ............. And the .......... Itself.
View SolutionIf one angle of a linear pair is acute, then its other angle will be ............. .
View SolutionIf a ray stands on a line, then the sum of the two adjacent angles so formed is............... .
View SolutionIf the sum of two adjacent angles is `180^@`, then the .........arms of the two angles are opposite rays.
View SolutionIf two lines intersect, then vertically opposite angles are......... .
View SolutionIn fig.
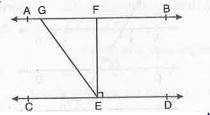 , if `AB II CD`, `EF _|_ CD` and `angleGED = 126^@`, find `angleAGE, angleGEF` and `angleFGE`.
, if `AB II CD`, `EF _|_ CD` and `angleGED = 126^@`, find `angleAGE, angleGEF` and `angleFGE`.
View SolutionIn fig.
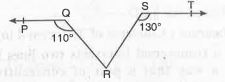 ,
,
if `PQ II ST`, `anglePQR = 110^@` and `angleRST = 130^@`, find `angleQRS`.
View SolutionIn fig.

, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray move along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB II CD.
View SolutionIn given fig.
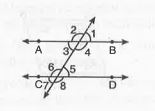 , given `AB || CD` if `angle1 = (120 -x)^@` and `angle5 = 5x^@`, find the measures of `angle1` and `angle5`.
, given `AB || CD` if `angle1 = (120 -x)^@` and `angle5 = 5x^@`, find the measures of `angle1` and `angle5`.
View SolutionIf two parallel lines are intersected by a transversal, then each pair of corresponding angles are .......... .
View SolutionIf two parallel lines are intersected by a a transversal, then interior angles on the same side of the transversal are ......... .
View SolutionTwo lines are perpendicular to the same line are ......... to each other.
View SolutionIf a transversal intersects a pair of lines in such a way that a pair of alternate angles are equal, then two lines are ......... .
View SolutionTwo lines parallel to the same line are ........... to each other.
View SolutionIf a transversal intersects a pair of lines in such a way that the sum of interior angles on the same side of the transversal is `180^@`, then the lines are .......... .
View SolutionIn the given fig.
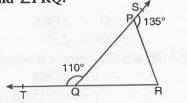 , sides QP and RQ of `DeltaPQR` aer produced to points S and T respectively. If `angleSPR = 135^@` and `anglePQT = 110^@`, find `anglePRQ`.
, sides QP and RQ of `DeltaPQR` aer produced to points S and T respectively. If `angleSPR = 135^@` and `anglePQT = 110^@`, find `anglePRQ`.
View SolutionIn the given fig.
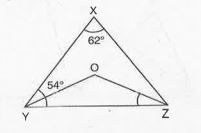 `angleX = 62^@`, `angleXYZ = 54^@`. If YO and ZO are the bisectors of `angleXYZ` and `angleXZY` respectively of `DeltaXYZ`, find `angleOZY` and `angleYOZ`.
`angleX = 62^@`, `angleXYZ = 54^@`. If YO and ZO are the bisectors of `angleXYZ` and `angleXZY` respectively of `DeltaXYZ`, find `angleOZY` and `angleYOZ`.
View SolutionIn the given Fig.
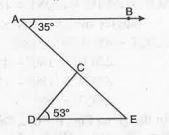 if `AB II DE`, `angleBAC = 35^@` and `angleCDE = 53^@`, find `angleDCE`.
if `AB II DE`, `angleBAC = 35^@` and `angleCDE = 53^@`, find `angleDCE`.
View SolutionIn the given Fig.
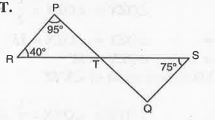 , if lines PQ and RS intersect at point T, such that `anglePRT = 40^@`, `angleRPT = 95^@` and `angleTSQ = 75^@` find `angleSQT`.
, if lines PQ and RS intersect at point T, such that `anglePRT = 40^@`, `angleRPT = 95^@` and `angleTSQ = 75^@` find `angleSQT`.
View SolutionIn the given Fig.
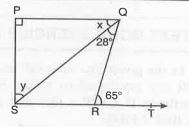 , if `PQ _|_PS`, `PQ II SR`, `angleSQR = 28^@` and `angleQRT = 65^@`, then find the values of x and y.
, if `PQ _|_PS`, `PQ II SR`, `angleSQR = 28^@` and `angleQRT = 65^@`, then find the values of x and y.
View SolutionIn Fig., the side QR of `DeltaPQR` is producted to a point S. If the bisectors of `anglePQR` and `anglePRS` meet at point T, then prove that
`angleQTR=1/2 angleQPR`.
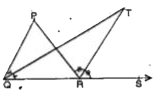
View SolutionIf the angles of triangle are in the ratio of `2 : 3 : 4`, find the three angles.
View SolutionProve that if one angle of a triangle is equal to the sum of the other two angles, the triangle is right angled.
View SolutionIn the given Fig
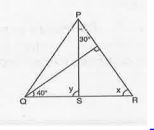 , if `QT _|_ PR`, `angleTQR = 40^@` and `angleSPR = 30^@`, find the value of x and y.
, if `QT _|_ PR`, `angleTQR = 40^@` and `angleSPR = 30^@`, find the value of x and y.
View SolutionIn the given figure
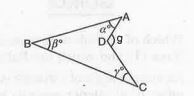 prove that `g = alpha + beta + gamma`.
prove that `g = alpha + beta + gamma`.
View SolutionIn given fig.
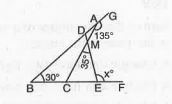 find x.
find x.
View SolutionProve that sum of all the interior angles of a pentagon is `540^@`.
View SolutionProve that the angle between internal bisector of one base angle and the external bisector of the other is equal to one-half of the vertical angles.
View SolutionIn the given Fig
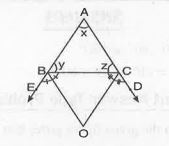 , Sides AB and AC of a `DeltaABC` are produced to E and D respectively. If respective bisectors BO and CO of `angleCBE` and `angleBCD` intersect each other at point O, prove that`angleBOC = 90^@-1/2 angleBAC`.
, Sides AB and AC of a `DeltaABC` are produced to E and D respectively. If respective bisectors BO and CO of `angleCBE` and `angleBCD` intersect each other at point O, prove that`angleBOC = 90^@-1/2 angleBAC`.
View SolutionAn exterior angle of a triangle is less than either of its interior opposite angles.
View SolutionSum of the three angles of a triangle is `180^@`.
View SolutionSum of the four angles of a quadrilateral is the four right angles.
View SolutionA triangle can have two right angles.
View SolutionA triangle can have two acute angles.
View SolutionA triangle can have two obtuse angles
View SolutionAn exterior angle of a triangle is equal to the sum of the two interior opposite angles.
View SolutionSum of the three angles of a triangle is .............. .
View SolutionAn exterior angle of a triangle is equal to the two ............. opposite angles.
View SolutionAn exterior angle of a triangle is always .................... than either of the interior opposite angles.
View SolutionA triangle cannot have more than ............ right angles
View SolutionA triangle cannot have more than ............ obtuse angles.
View SolutionSum of the angles of a quadrilateral is ................ .
View SolutionIn fig.
 AB and CD intersect each other at point O. If `angleAOC + angleBOE = 70^@` and `angleBOD = 40^@` then the value of `angleBOE` and reflex `angleCOE` are :
AB and CD intersect each other at point O. If `angleAOC + angleBOE = 70^@` and `angleBOD = 40^@` then the value of `angleBOE` and reflex `angleCOE` are :
View SolutionIn fig.
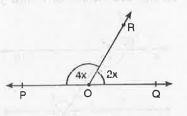 POQ is a line, `anglePOR = 4x` and `angleQOR = 2x` then the value of x is :
POQ is a line, `anglePOR = 4x` and `angleQOR = 2x` then the value of x is :
View SolutionIn the given fig.
 if `angleAOC + angleBOD = 75^@` then the value of `angleCOD` is :
if `angleAOC + angleBOD = 75^@` then the value of `angleCOD` is :
View SolutionIn the fig.
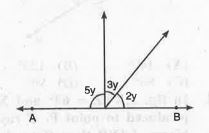 value of y is :
value of y is :
View SolutionIn the given fig.
 the value of x is :
the value of x is :
View SolutionIn fig. , `anglePOR and angleQOR` form a linear pair if `a -b = 80^@` then values of a and b are :
View SolutionIn fig.
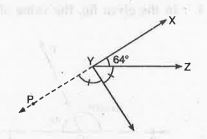 `angleXYZ = 64^@` and XY is produced to point P. If ray YQ bisect `angleZYP` then the value of `angleXYQ` is :
`angleXYZ = 64^@` and XY is produced to point P. If ray YQ bisect `angleZYP` then the value of `angleXYQ` is :
View SolutionIn fig.
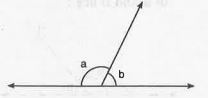 , b is more than one-third of a right angle than a. The values of a and b are :
, b is more than one-third of a right angle than a. The values of a and b are :
View SolutionIn fig.
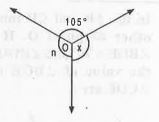 `n - x = 3^@` then values of x and n are :
`n - x = 3^@` then values of x and n are :
View SolutionFor parallel lines the sum of interior angles on the same side of a transversal is :
View SolutionIn fig.
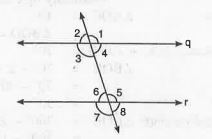 `q II r` and p is transversal. If `angle1` and `angle2, 3 : 2` then the values of `angle3` and `angle4` are :
`q II r` and p is transversal. If `angle1` and `angle2, 3 : 2` then the values of `angle3` and `angle4` are :
View SolutionIn fig. the values of x and y are :
View SolutionIn fig.
 , if `AB || CD`, `CD ||EF` and `y : z = 3 : 7` then value of x is :
, if `AB || CD`, `CD ||EF` and `y : z = 3 : 7` then value of x is :
View SolutionIn fig.
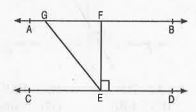 , if `AB ||CD`, `EF _|_ CD` and `angleGED = 126^@` then the value of `angleAGE` is :
, if `AB ||CD`, `EF _|_ CD` and `angleGED = 126^@` then the value of `angleAGE` is :
View SolutionIn fig.
 ,
,
if `PQ II ST`, `anglePQR = 110^@` and `angleRST = 130^@`, find `angleQRS`.
View SolutionIn fig.
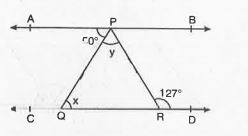 , if `AB || CD`, `angleAPQ = 50^@` and `anglePRD = 127^@` then values of x and y are :
, if `AB || CD`, `angleAPQ = 50^@` and `anglePRD = 127^@` then values of x and y are :
View SolutionIn fig
 , `AB||CD`, the value of x is :
, `AB||CD`, the value of x is :
View SolutionFor two parallel lines sum of interior angles on the same side of a transversal, is .............. .
View SolutionIn fig.
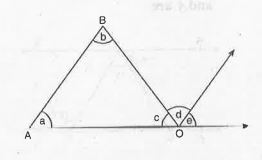 , the sum of `anglea` and `angleb` is :
, the sum of `anglea` and `angleb` is :
View SolutionIn a triangle interior opposite angle is always less than :
View SolutionIn a triangle sum of two interior angles is always equal to :
View SolutionIn fig.
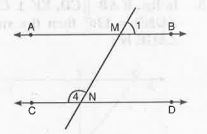 , `angle1 = 70^@` then the value of `angle4` is :
, `angle1 = 70^@` then the value of `angle4` is :
View SolutionIn a triangle exterior angle is always greater than :
View SolutionIn fig.
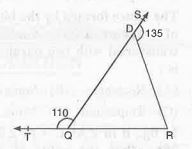 , the sides QP and RQ of a `DeltaPQR` are produced to points S and T respectively. If `angleSPR = 135^@` and `anglePQT = 110^@` then the value of `anglePRQ` is :
, the sides QP and RQ of a `DeltaPQR` are produced to points S and T respectively. If `angleSPR = 135^@` and `anglePQT = 110^@` then the value of `anglePRQ` is :
View SolutionIn the given fig.
 `angleX = 62^@`, `angleXYZ = 54^@`. If YO and ZO are the bisectors of `angleXYZ` and `angleXZY` respectively of `DeltaXYZ`, find `angleOZY` and `angleYOZ`.
`angleX = 62^@`, `angleXYZ = 54^@`. If YO and ZO are the bisectors of `angleXYZ` and `angleXZY` respectively of `DeltaXYZ`, find `angleOZY` and `angleYOZ`.
View SolutionIn fig.
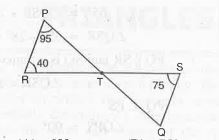 , if lines PQ and RS intersect each other at point T such that `anglePRT = 40^@`, `angleRPT = 95^@` and `angleTSQ = 75^@` then the value of `angleSQT is :
, if lines PQ and RS intersect each other at point T such that `anglePRT = 40^@`, `angleRPT = 95^@` and `angleTSQ = 75^@` then the value of `angleSQT is :
View SolutionIn fig.
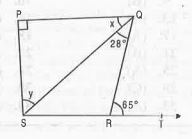 , if `PQ _|_ PS`, `PQ ||SR`, `angleSQR = 28^@` and `angleQRT = 65^@` then the values of x and y are :
, if `PQ _|_ PS`, `PQ ||SR`, `angleSQR = 28^@` and `angleQRT = 65^@` then the values of x and y are :
View Solution
Exercise questions and complete solutions for chapter Lines and Angles of MBD of Class 9