Complete Solutions to EXAMPLE of chapter LINES AND ANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | LINES AND ANGLES |
| MODERN PUBLICATION | EXAMPLE |
| Number Of Questions | 81 |
| Academic Year | 2023-24 |
Find the measure of an angle, which is
complement of itself?
View SolutionFind the measure of an angle, which is
supplement of itself?
View SolutionAn angle equal to four times its complement. Find its measure.
View SolutionAn angle equal to four times its complement. Find its measure.
View SolutionFind the measure of the angle, which more than is complement.
View SolutionWhat is the measure of angle which is `45 ^(@)` less than twice its supplement ?
View SolutionIn the fig. `angleAOC` and `angleBOC` from a linear pair. Find the value of x
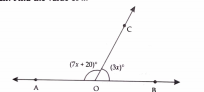
View SolutionIn the fig. AOB is a straight line. Find `angleAOC` and `angleBOD`
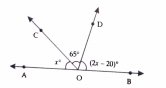
View SolutionIn the figure AOB is a straight lne, `angle COD=90^@,angleBOE=72^@`, find `angleAOC,angleBOD` and `angleAOE`.
View SolutionIf ray OC stands on line AB such that `angleAOC = angleBOC` (see fig.
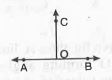 ) show that `angleAOC = 90^@`.
) show that `angleAOC = 90^@`.
View SolutionIn the fig. find the value of x

View SolutionIn the fig. lines AC and BD intersect at O. if `angleAOD: angleDOC=4:5` then find `angleCOB`.
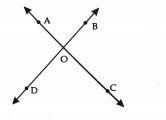
View SolutionProve that the bisectors of the angles of a linear pair are at right angles.
View SolutionProve that the bisectors of a pair of vertically opposite angles are in the same striaght line.
View SolutionTwo lines, which are both parallel to the same line, are parallel to each other, prove that.
View SolutionIf a line is perpendicular to one of two given parallel lines, then prove that it is also perpendicular to the other line.
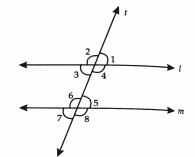
View SolutionIn the fig. l||m, `angle1` and `angle2` are in the ratio 5:4. find `angle3` and `angle4`
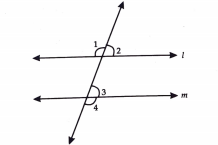
View SolutionIn the fig. `angle3=63^@` and `angle8=115^@`. Is l||m?
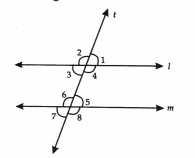
View SolutionIn the fig. AB||CD. Determine `anglex`
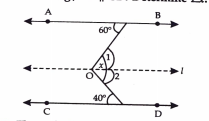
View SolutionIn the fig. l||m angle 1 and 2 are in the ratio 2:3. find all the angles
View SolutionIn the fig. AB||CD. Find the value of x
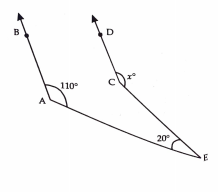
View SolutionIn the fig. AB||CD find the value of x
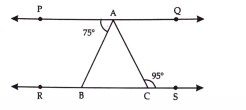
View SolutionIn the fig. PQ||RS, `anglePAB=75^@` and `angleACS=95^@, then, value, of, angleBAC` and `angleCAQ`.
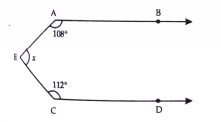
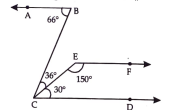
View SolutionIn the fig. show that AB||EF
View SolutionIn the fig. lines AB and CD are parallel and P is at any point beween the two lines. Prove that:
`angleABP+angleCDP=angleDPB`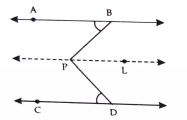
View SolutionIn Fig. 6.33, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD.

View SolutionThe angles of triangle are `(x-40)^@`, `(x-20)^@` and `(1/2x-10)^@`. Find x.
View SolutionThe angles of a triangle are in the ratio 2:3:7. find the three angles.
View SolutionIn a `triangleABC`, if `2A=3angleB=6angleC`, calculate the measures of `angleA,angleB` and `angleC`.
View SolutionA,B and C are three angles of a triangle `A-B=15^@,B-C=30^@`, find `angleA,angleB` and `angleC`
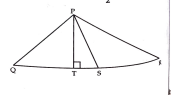
View SolutionIn the fig. PS is the bisector of `angleQPR` and `PTbotQR`. Prove that `angleTPS=1/2(angleQ-angleR)`
View SolutionShow that the bisectors of the base angles of a triangle can never enclose a right angle.
View SolutionIn the fig. side BC of `triangleABC` is produced to from ray BD and CE||BA
Prove that `angleACD=angleA+angleB`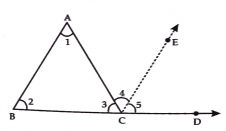
View SolutionIn the fig.
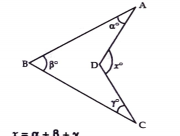
Prove that `x=alpha+beta+gamma`
View SolutionIn the fig. `traingleABC` is an isosceles triangle in which AB=AC and AE bisects `angleCAD`. Prove that
AE||BC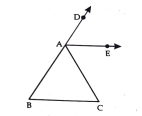
View SolutionIn the fig. prove that p||m

View SolutionIn both of the following figures AB||CD find the value of x. define x in each case
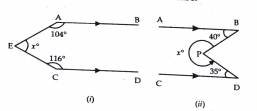
View SolutionIn the figure, AB||CD find the value of x
View SolutionIn fig, AD and CE are the angle bisectors of `angleA` and `angleC` respectively. If `angleABC=90^@` then find the `angleAOC`

View SolutionProve that the bisectors of the angles of a linear pair are at right angles.
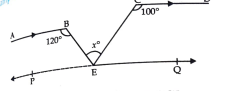
View SolutionIn the figure, AB||CD find the value of x

View SolutionIn Fig.
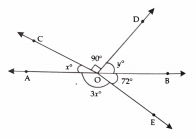
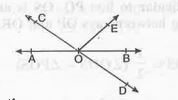 , lines AB and CD intersect at O. If `angleAOC+angleBOE=70^@` and `angleBOD = 40^@`, find `angleBOE` and reflex `angleCOE`.
, lines AB and CD intersect at O. If `angleAOC+angleBOE=70^@` and `angleBOD = 40^@`, find `angleBOE` and reflex `angleCOE`.
View SolutionIn fig. lines XY and MN intersect at O. if `anglePOY=90^@` and a:b=2:3, find c

View SolutionIn fig. lines `anglePQR=anglePRQ`, then prove that `anglePQS=anglePRT`
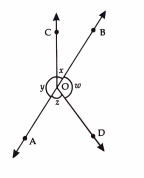
View SolutionIn fig. if x+y=w+z, then prove that AOB is a line
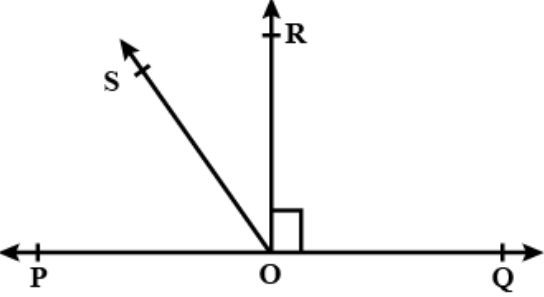
View SolutionIn Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that `angle ROS=1/2 (angle QOS-angle POS)`.
View SolutionIt is given that `/_XYZ = 64^@` and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects `/_ZYP`, find `/_XYQ `and reflex `/_QYP`.
View SolutionIn fig. find the value of x and y and then show that AB||CD
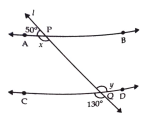
View SolutionIn fig. AB||CD, CD||EF and y:z=3:7, find x
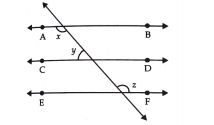
View SolutionIn fig. AB||CD, `EFbotCD` and `angleGED=126^@`, find `angleAGE,angleGEF` and `angleFGE`
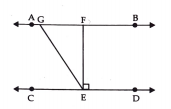
View SolutionIn fig. PQ||ST=`110^@`, and `angleRST=130^@`, find `angleQRS`
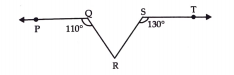
View SolutionIn fig. if AB||CD, `angleAPQ=50^@` and `anglePRD=127^@` find x and y
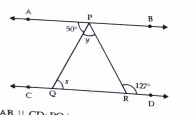
View SolutionIn the given fig.
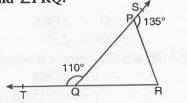 , sides QP and RQ of `DeltaPQR` aer produced to points S and T respectively. If `angleSPR = 135^@` and `anglePQT = 110^@`, find `anglePRQ`.
, sides QP and RQ of `DeltaPQR` aer produced to points S and T respectively. If `angleSPR = 135^@` and `anglePQT = 110^@`, find `anglePRQ`.
View SolutionIn the given fig.
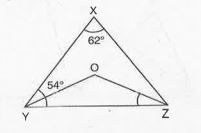 `angleX = 62^@`, `angleXYZ = 54^@`. If YO and ZO are the bisectors of `angleXYZ` and `angleXZY` respectively of `DeltaXYZ`, find `angleOZY` and `angleYOZ`.
`angleX = 62^@`, `angleXYZ = 54^@`. If YO and ZO are the bisectors of `angleXYZ` and `angleXZY` respectively of `DeltaXYZ`, find `angleOZY` and `angleYOZ`.
View SolutionIn the given Fig.
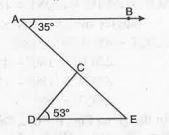 if `AB II DE`, `angleBAC = 35^@` and `angleCDE = 53^@`, find `angleDCE`.
if `AB II DE`, `angleBAC = 35^@` and `angleCDE = 53^@`, find `angleDCE`.
View SolutionIn the given Fig.
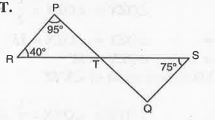 , if lines PQ and RS intersect at point T, such that `anglePRT = 40^@`, `angleRPT = 95^@` and `angleTSQ = 75^@` find `angleSQT`.
, if lines PQ and RS intersect at point T, such that `anglePRT = 40^@`, `angleRPT = 95^@` and `angleTSQ = 75^@` find `angleSQT`.
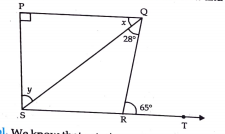
View SolutionIn fig. `PQbotPS,PQ||SR`, `angleSQR=28^@` and `angleQRT=65^@` then find the values of x and y
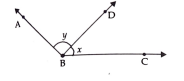
View SolutionFor what value of x+y in Fig. will ABC be a line? Justify your answer
View SolutionCan you have a triangle with all the three angles less than `60^@`?
View SolutionA triangle can have two obtuse angles
View SolutionHow many triangles can be drawn having its angles as `45^@,64^@` and `72^@`? Give reasons for your answer.
View SolutionHow many triangles can be drawn having its angles as `53^@,64^@` and `63^@`? Give reason for your answer.
View SolutionIf one of the angles formed by two intersecting lines is a right angle, what can you say about the other three angles? Give reasonf for your answer.
View SolutionTwo adjacent angles are equal. Is its necessary that each of these angles will be a right angle?
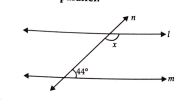
View SolutionIn fig. find the value of x for which the lines l and m are parallel
View SolutionIn the given figures which of the following two lines are parallel and why?
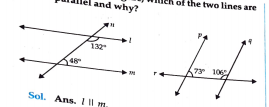
View SolutionTwo lines are perpendicular to the same line are ......... to each other.
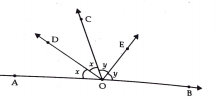
View SolutionIn fig. OD is the bisector of `angleAOC`, OE is the bisector of `angleBOC` and `ODbotOE`. Show that the points A,O and B are collinear
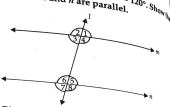
View SolutionIn fig. `angle1=60^@` and `angle6=120^@` show that the lines m and n are parallel
View SolutionAP and BQ are the bisects of the two alternate interior angles formed by the intersection and a transversal t with parallel lines l and m show in figure, show that AP||BQ
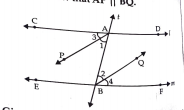
View SolutionIn fig. Bisectos AP and BQ of the alternate interior angles are parallel then show that l||m
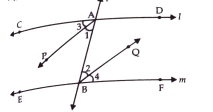
View SolutionIn fig. BA||ED and BC||EF. Show that `angleABC=angleDEF`

View SolutionIn fig. BA||ED and BC||EF> show that `angleABC+angleDEF=180^@`
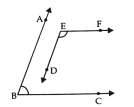
View SolutionThe angles of a traingle are in the ratio 2:3:4. find the angles of the triangle.
View SolutionA triangle ABC is right angled at A. AM is drawn perpendicular to BC. Prove that `angleBAM=angleACB`
View SolutionIf a line is perpendicular to one of two given parallel lines, then prove that it is also perpendicular to the other line.
View SolutionFill in the blanks:
If two lines intersect at a point, then the vertically opposite angles are always_____________.
View SolutionBisectors of interior `angleB` and exterior `angleACD` of a `triangleABC` intersect at the point T. prove that `angleBTC=1/2angleBAC`.
View SolutionProve that through a given point, we can draw only perpendicular to a given line.
View SolutionIf a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel.
View SolutionA triangle can have two acute angles.
View Solution
EXAMPLE questions and complete solutions for chapter LINES AND ANGLES of MODERN PUBLICATION of Class 9