Complete Solutions to EXERCISE of chapter TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIANGLES |
| MODERN PUBLICATION | EXERCISE |
| Number Of Questions | 98 |
| Academic Year | 2023-24 |
PQR is a triangle in which PQ=PR and S is any point on the side PQ. Through S, a line is drawn parallel to QR and intersecting PR at T. prove that PS=PT.
View SolutionIn an isosclees triangle ABC, with AB = AC, the bisectors of `angleB` and `angleC` intersect each other at O. Join A to O show that : AO bisects `angleA`.
View SolutionP is a point on the bisector of an angle `angleABC`. If the line through P parallel to AB meets BC at Q. prove that triangle BPQ is isosceles.
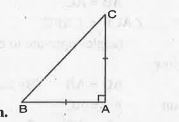
View SolutionABC is a right angled triangle in which `angleA = 90^@` and AB = AC. Find `angleB` and `angleC`.
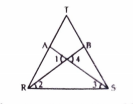
View SolutionIn the fig. RT=TS, `angle1=2angle2` and `angle4=2angle3`. Prove that `triangleRBTequivtriangleSAT`
View SolutionIn the fig AB=CD and AD=BC. Prove that `triangleADCequivtriangleCBA`

View SolutionIn `trianglePQR`, S is the point on the side QR. Prove that PQ+QR+RP>2PS
View SolutionIn the given fig. O is the point of each of the line segment AB and CD prove that AC=BD and AD||BD

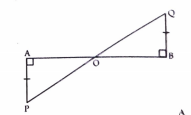
View SolutionIn the given figure `PA bot AB`, `QB bot AB` and PA=QB intersects AB at O, show that O is the mid point of AB as well as that of PQ
View SolutionIn the fig. X and Y are respectively two points on equal sides AB and AC of `triangleABC` such that AX=AY. Prove that CX=BY

View SolutionIn the fig. C is the mid point of AB. If `angleDCA=angleECB` and `angleDBC=angleEAC`, prove that DC=EC
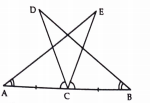
View SolutionIn the fig. `BAbotAC` and `DEbotEF` such that BA=DE and BF=DC. Prove that AC=EF
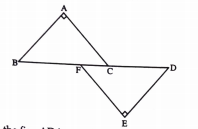
View SolutionIn the fig. AD is a median of `triangleABC`. If BL and CM are drawn perpendicular on AD and AD produced, prove that BL=CM
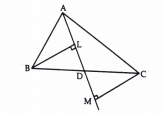
View SolutionIn the fig. triangle AB=AC and bisectors of `angleB` and `angleC` meet at a point O. prove that BO=CO and the ray AO is bisector of angleA
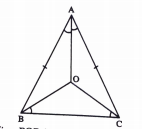
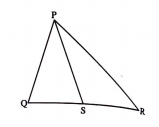
View SolutionIn the fig, PQR is an equilateral triangle and QRST is a square. Prove that:
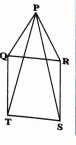
PT=PS
View SolutionIn the fig, PQR is an equilateral triangle and QRST is a square. Prove that:
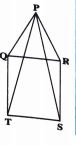
`anglePSR=15^@`
View SolutionProve that the median from the vertex of an isosceles triangle is the bisector of the vertical angle.
View SolutionIn the fig. ABCD is square and P is a point on such that PB=PD. Prove that CPA is a striaght line

View SolutionIn the fig. :ABCD is a quadrilateral in which AD=AB and BC=DC. Prove that
AC bisects `angleA=angleC`
View SolutionIn the fig. :ABCD is a quadrilateral in which AD and BC=DC. Prove that
AC is the perpendicular bisector of BD.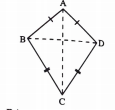
View SolutionIn the fig. P is a point in the interior of `angleAOB`, `PLbotOA` and `PMbotOB` such that PL=PM, show OP is the bisector of `angleAOB`
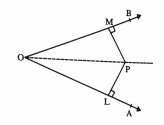
View SolutionIn the fig. ABCD is a square M is the mid point and `PQ bot CM` meets AD at and CB produced prove that

PA=BQ?
View SolutionIn the fig. ABCD is a square M is the mid point and `PQ bot CM` meets AD at and CB produced prove that

PA=BQ?
View SolutionIn triangle ABC, if `angleA=40^@` and `angleB=60^@`. Determine the longest and shortest sides of the triangle.
View SolutionIn `triangle ABC`, if `angleA=90^@` and `angleB=35^@` which is the longest side?
View SolutionIn `triangleABC`, if `angleB=angleC=45^@`which is the longest side?
View SolutionIs it possible to draw a triangle with sides of the lenghts 2 cm, 3 cm and 7 cm?
View SolutionIn `triangleABC`, side AB is produced to D such that BD=BC. If `angleB=60^@` and `angleA=70^@`, prove that:
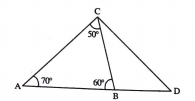
AD>CD?
View SolutionIn `triangleABC`, side AB is produced to D such that BD=BC. If `angleB=60^@` and `angleA=70^@`, prove that:

AD>CD?
View SolutionIn `triangleABC`, if the AD is a bisector of `angleA` show that AB>BD and AC>CD
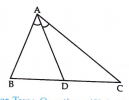
View SolutionIn the fig. AC>AB and AD is the bisector of `angleA` show that `angleADC>angleADB`
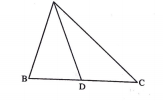
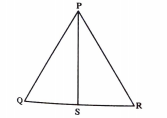
View SolutionIn the `trianglePQR`, S is any point on the side QR show that PQ+QR+RP+2PS
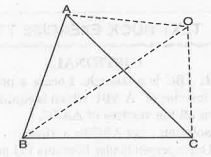
View SolutionO is any point in the exterior of a `DeltaABC`. Prove that `2(OA + OB + OC) > (AB + BC + CA)`
 .
.
View SolutionO is any point in the exterior of a `DeltaABC`. Prove that `2(OA + OB + OC) > (AB + BC + CA)`
 .
.
View SolutionO is any point in the exterior of a `DeltaABC`. Prove that `2(OA + OB + OC) > (AB + BC + CA)`
 .
.
View SolutionIn the fig. O is the centre of the circle and XOY is diameter. If XZ is any other chord of the circle show that XY>XZ
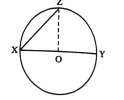
View SolutionThe measure of each angle of an equilateral triangle is :
View SolutionIn two triangles, ABC and ADC, if AB=AD, BC=CD. Are they congruent?
View SolutionIf two congruent triangles ABC and DEF, if AB=DE and BC=EF. Name the pairs of equal angles.
View SolutionIn two triangles ABC and DEF,
`angleA=angleD,angleB=angleE` and `angleC=angleF and AB=3DE`. Then the two triangles are:
View SolutionABC is an isosceles triangle AB=AC and BD and CE are its two medians. Show that BD=CE.
View SolutionCDE is an equilateral triangle formed on a side CD of a square ABCD(see fig.). Show that `triangleADEqequivtriangleBCE`
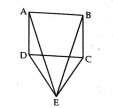
View SolutionIn the fig. prove that:
AD+AB+BC+CD>2AC.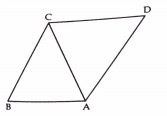
View SolutionIn the fig. find x and y
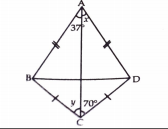
View SolutionABC is an isosceles triangle with AB = AC and AD is one of its altitudes.
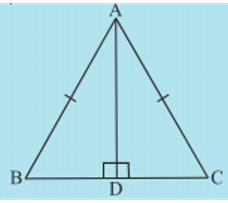
Is `triangleADB ~= triangleADC`? Why or why not?
View SolutionIn `triangleABC`, AB=AC and `angleA=100^@`, find `angleB` and `angleC`.
View SolutionSum of any two sides of a triangle is greater than the third side.
View SolutionIn a triangle, the angle opposite to the longer side is :
View SolutionThe sides opposite to two equal angles of a triangle are :
View SolutionIf altitudes from two vertices of a triangle to the opposite sides are equal prove that the triangle is isosceles.
View SolutionState True or false
Bisectors of unequal angle of an triangle may be equal.
View SolutionIn `triangleABC,A=46^@,B=74^@` then find angle C
View SolutionIf two right triangles, one side and an acute angle of one triangle are equal to one side and the corresponding angle of other triangle. Prove that the two triangles are congruent.
View SolutionTrue or False :ASA is not a Congruent Criteirorn.
View Solutionan equilateral triangle?
View SolutionBy ASA Congruence Criterion, two angls and included side of one triangle are equal to the corresponding angles and included side of other triangles.
View SolutionSides opposite to…………..angles to a triangle are equal.
View SolutionA `triangleABC` is obtuse angled at point B then the longest side is………….
View SolutionIf in two triangles `trianglePQR` and `triangleDEF`, PR=EF, QR=DE,PQ=FD, then `trianglePQRequiv…………….` ..
View SolutionIn an equilateral triangles all angles are……………. .
View SolutionDifference of any two sides of a triangle is equal to the third side.
View SolutionShow that in a right angled triangle, the hypotenuse is the longest side.
View SolutionThe sum of three altitudes of a triangle is ........... Than its perimeter.
View SolutionIn right `triangleABC` and `triangleDEF`, if hypotenuse AB=EF and side AC=DE, then `deltaABCequiv`………….
View SolutionIf in two triangles `triangleABC` and `trianglePQR`, AB=QR `angleA=angleQ` and `angleB=angleR`, then `triangleABCequiv……………..` .
View SolutionA triangle with sides measuring 6cm, 5 cm and 12 cm is……………..to draw.
View SolutionWhich of the following is not a criteria for congruence of triangles?
View SolutionIf AB=QR, BC=PR and CA=PQ then
View SolutionIn `triangleABC`, AB=AC and `angleB=50^@`. Then the sum of angle C and A is equal to
View SolutionIn `triangleABC`, BC=AB and `angleB=80^@` then `angleA` is equal to
View SolutionIn `trianglePQR, angleR=angleP` and QR=4 cm and PR=5cm. Then the length of PQ is
View SolutionD is a point on the side BC of a triangle ABC such that `angleADC` = `angleBAC` . Show that `CA^2` = CB. CD.
View SolutionIt is given that `triangleABC=triangleFDE` and AB=5 cm, `angleB=40^@` and `angleA=80^@`. Then which of the following is true?
View SolutionTwo sides of a triangle are of lenghts 5 cm and 1.5 cm. the length of the third side of the cannot be
View SolutionIn `DeltaPQR`, If `angleR > angleQ`, then :
View SolutionIn `DeltaABC` and PQR, AB = AC, `angleC = angleP` and `angleB = angleQ`. The two triangles are :
View SolutionIn triangles ABC and DEF, AB=FD, `angleA=angleD`. The two triangles will become congurent by SAS axiom if
View SolutionWhich is true?
View SolutionIn `trianglesABC` and `trianglePQR`, it is given that AB=AC, `angleC=angleP` and `angleB=angleQ`. Then the two triangles are
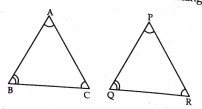
View SolutionIn `triangleABC` and `triangleDEF`, it is given that `angleB=angleE` and `angleC=angleF`. In order that `triangleABCequivtriangleDEF`. We must have

View SolutionIn `triangleABC` and `triangleDEf`, it is given that AB=DE and BC=EF in order that `triangleABCequivtrianleDEF`, we must have to

View SolutionIf `triangleABCequivtriangleLKM`, then which side of `triangleLKM` equal to sides of AC of `triangleABC` is
View SolutionIf `triangleABC` and PQR if `angleA=angleR`, `angleB and angle P` and AB=RP, then which one of the following congruence conditions applies
View SolutionIn `trianglePQRequivtriangleEFD`, then `angleE=`
View SolutionIn an isosceles triangle, if the vertex angle is equal to the sum of the base angles, then the measure vertex angles of the triangles is
View SolutionWhich of the following is not true
View SolutionIn `triangleABC`, AB=AC and `angleA=100^@`, find `angleB` and `angleC`.
View SolutionIn `trianglePQR` what is the value of x
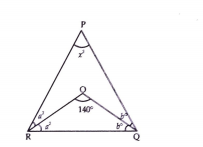
View SolutionO is any point in the interior of `triangleABC` such that OB=OC and AB=AC. Show that AO bisects `angleA`.
View SolutionIn `triangleABC,angleB=35^@,angleC=65^@` and the bisector of `angleBAC` meets in X. arrange AX,BX and CX in descending order.
View SolutionABC is an isosceles triangle with AB = AC and AD is one of its altitudes.

Is BD = CD? Why or why not?
View SolutionCDE is an equilateral triangle formed on a side CD of a square ABCD(see fig.). Show that `triangleADEqequivtriangleBCE`

View SolutionCDE is an equilateral triangle formed on a side CD of a square ABCD(see fig.). Show that `triangleADEqequivtriangleBCE`

View SolutionD is any point on side AC of `triangleABC` with AB=AC show that CD>BD.
View SolutionBisectors of angles B and C of an isoscels triangles ABC with AB=AC intersects each other at O. prove that external angle adjacent to `angleABC` is equal to `angleBOC`.
View SolutionABC is a right angled with AB=AC. Bisector of `angleA` meets BC at D. prove that BC=2AD
View SolutionO is a point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that `triangleOCD` is an isosceles triangle.
View SolutionIn a triangle ABC, D is the mid point of side AC such that `BD=1/2AC`. Show that `angleABC` is a right angle.
View Solution
EXERCISE questions and complete solutions for chapter TRIANGLES of MODERN PUBLICATION of Class 9