Complete Solutions to EXAMPLE of chapter TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIANGLES |
| MODERN PUBLICATION | EXAMPLE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
In `DeltaABC, angleA=120^@` and AB=AC. Find `angleB` and `angleC`
01:40View SolutionThe measure of each angle of an equilateral triangle is :
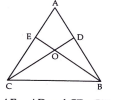
01:33View SolutionIn the fig AE=AD and BD=CE. Prove that `triangleAEBequivtriangleADC`
 02:23View Solution
02:23View SolutionIf the bisector of an angle of a triangle also bisects the opposite side, prove that triangle is isosceles.
02:56View Solutionan equilateral triangle?
02:03View SolutionIn a rt. triangle if acute angle is double of other angle then hypotenuse is :
06:10View SolutionIf M is the mid point of hypotenuse AC of rt. `DeltaABC` then `BM = 1/2.....`
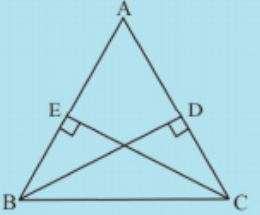
07:29View SolutionIn Fig, BD and CE are altitudes of `triangleABC` such that BD = CE.
Is `angleDCB = angleEBC`? Why or why not?
 02:03View Solution
02:03View SolutionUsing vector method, prove that the altitudes of a triangle are concurrent.
03:10View SolutionIf altitudes from two vertices of a triangle to the opposite sides are equal prove that the triangle is isosceles.
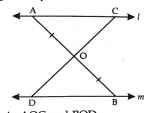
02:35View SolutionIf AB is a line segment AX and BY are two equal and line segments drawn on opposite sides of the line AB such that AX||BY. If the AB and XY intersect and each other at O, prove that
`triangleAOXequivtriangleBOY`.03:21View SolutionIf AB is a line segment AX and BY are two equal and line segments drawn on opposite sides of the line AB such that AX||BY. If the AB and XY intersect and each other at O, prove that
AB and XY bisect each other.03:32View SolutionIf two right triangles, one side and an acute angle of one triangle are equal to one side and the corresponding angle of other triangle. Prove that the two triangles are congruent.
03:26View SolutionIn the fig. AB=AC and DB=DC. Prove that `angleABD=angleACD`
 01:52View Solution
01:52View SolutionIn the fig. l||m and O is the mid point of the line segment. Prove that O is also the mid point of any line segment CD having its end points on l and m respectively
 02:10View Solution
02:10View SolutionIn the fig. BL and DM are bisector perpendicular to the segment AC and BL=DM find that AC bisects BD
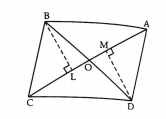 02:58View Solution
02:58View SolutionIn the fig. ABC is a triangle in which AB=AC side BA is produced to D such that AB=AD prove that `angle=BCD=90^@`
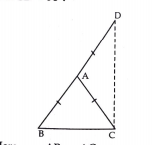 02:39View Solution
02:39View SolutionSides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of `trianglePQR` (see Fig.). Show that `triangleABC ~ trianglePQR` .
 .05:59View Solution
.05:59View SolutionIn the fig. `angleA=angleC` and AB=BC. Prove that `triangleABDequivtriangleCBE`
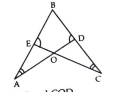 01:12View Solution
01:12View SolutionIn the fig. AB=EF, BC=DE, `AB bot BD` and `EF bot CE`. Prove that triangleABD `equiv` triangleFEC
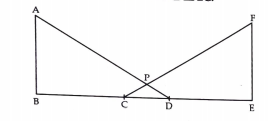 02:50View Solution
02:50View SolutionIn the fig. `angleQPR=anglePQR` and L and M are respectively on sides QR and PR of PQR such that QL=PM prove that OP=OQ, where O is the point of intersection of PL and QM
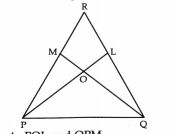 04:48View Solution
04:48View SolutionIn the fig. AB=CD and AD=BC prove that `triangleADCequivtriangleCBA`
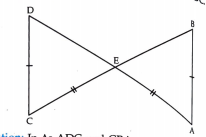 02:37View Solution
02:37View SolutionABCD is a parallelogram. If two diagonal are equals, find the measure of `angleABC`
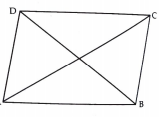 01:41View Solution
01:41View SolutionIN the fig. AD=BC and BD=CA. prove that `angleADB=angleBCA` and `angleDAB=angleCBA`
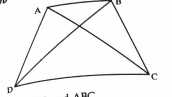 04:02View Solution
04:02View SolutionIn the fig. AB=AC , D is the point in the interior of `triangleABC` such that `angleDBC=angleDCB`. Prove that AD bisects `angleBAC` and `triangleABC`
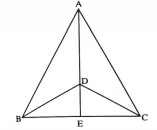 02:41View Solution
02:41View SolutionSet up an equation in the following cases:
In an isosceles triangle, the vertex angle is twice either base angle. (Let the base angle be b in degrees. Remember that the sum of angles of a triangle is 180 degrees).01:25View SolutionAD,BE and CF the altitudes of `triangleABC` are equal, prove that `triangleABC` is equilateral.
04:40View SolutionIn the fig. LM=MN, QM=MR,ML`bot`PQ and `MNbotPR`. Prove that PQ=PR
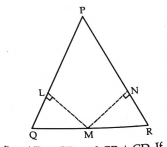 04:01View Solution
04:01View SolutionIn the fig. `ADbotCD` and `CBbotCD`. If AQ=BP and DP=CQ prove that `angleDAQ=angleCBP`.
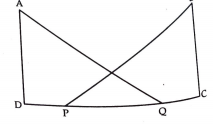 02:22View Solution
02:22View SolutionABC s a triangle and D is mid-point of BC. Perpendiculars froms D to AB and AC are equal. Prove that triangle is isosceles.
03:00View SolutionIf perpendiculars from any point within an angle on its forms arms are congruent prove that it lies on the bisector of that angle.
03:04View SolutionABC is a triangle in which BE and CF are perpendiculars to AC and AB respectively. If BE=CF, prove that `triangleABC` is isosceles.
02:33View SolutionIn a triangle ABC, if `angleA=50^@` and `angleB=60^@`, then which side of the triangle is longest and which side is shortest?
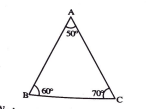 03:16View Solution
03:16View SolutionIn fig.
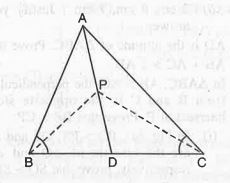 BP and CP are the bisectors of `angleB` and `angleC` respectively and AC > AB. Prove each of the following : `PC>PB`.05:39View Solution
BP and CP are the bisectors of `angleB` and `angleC` respectively and AC > AB. Prove each of the following : `PC>PB`.05:39View SolutionD is any point on the base BC, produced of an isosceles triangle ABC, prove that AD>AB.
04:35View SolutionProve that the sum of any two sides of a triangle is greater than twice the median drawn to the third side.
05:23View SolutionThe sum of three altitudes of a triangle is ...... The sum of its three sides.
05:49View SolutionThe perimeter of a triangle is ................... than the sum of its medians.
00:55View SolutionIn `trianglePQR`, S is the point on the side QR. Prove that PQ+QR+RP>2PS
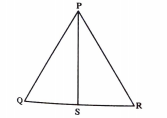 01:31View Solution
01:31View SolutionIn the `APbotQR`, PR>PQ and PS=PQ. Prove that AR>AQ
 01:16View Solution
01:16View SolutionIn the fig. AC>AB and D is the point on AC such that AB=AD. Show that BC>CD
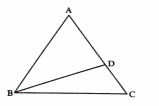 02:07View Solution
02:07View SolutionIn fig. ABCD is a quadrilateral and L and M are respectively points on AD and CD such that AB=BC,`angleABL=angleCBM` and `angleLBD=angleMBD`. Prove that BL=BM.
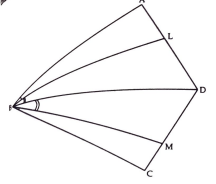 10:51View Solution
10:51View SolutionIn a rt. triangle if acute angle is double of other angle then hypotenuse is :
06:10View SolutionIf two isosceles triangles have a common base, prove that the line segment joining their vertices bisects the common base at right angles.
06:09View SolutionIn fig. PQRS is a quadrilateral in which diagonals PR and QS intersect at O
Show that:
PQ+QR+RS+SP>PR+QS01:33View SolutionIn fig. PQRS is a quadrilateral in which diagonals PR and QS intersect at O
Show that:
PQ+QR+RS+SP<2(PR+QS)04:01View SolutionA point O is taken inside the third PQRS such that its distance from the angular point and R is equal. Show that QO and SO are in ordinate the same striaght line i.e. points Q,O and R are collinear
 02:48View Solution
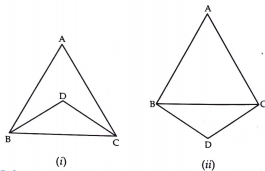
02:48View SolutionIn quadrilateral ACBD, AC = AD and AB bisects `angle A` (see Fig. 7.16). Show that `triangle ABC cong triangle ABD`. What can you say about BC and BD?
02:19View SolutionABCD is a quadrilateral in which AD=BC and `angleADB=angleCBA`. Prove that:
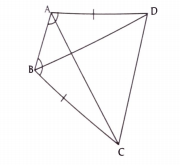
`triangleABD=triangleBAC`01:41View SolutionABCD is a quadrilateral in which AD=BC and `angleADB=angleCBA`. Prove that:

BD=AC02:08View SolutionABCD is a quadrilateral in which AD=BC and `angleADB=angleCBA`. Prove that:
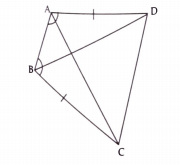
`angleABD=angleBAC`02:12View SolutionAD and BC are equal perpendicular to a line segment AB. Show that CD bisects AB
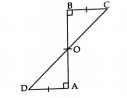 01:45View Solution
01:45View Solutionl and m are two parallel line intersects by another point of parallel lines p and q show that `triangle ABC equiv triangleCDA`
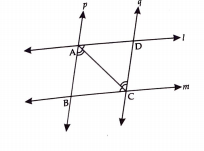 01:52View Solution
01:52View SolutionLine l is the bisector of an angle `angleA` and B is any point on l. BP and BQ are perpendiculars from B to the arms of `angleA` show that:
`triangleAPBequivtriangleAQB`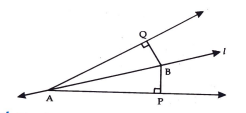 01:48View Solution
01:48View SolutionLine l is the bisector of an angle `angleA` and B is any point on l. BP and BQ are perpendiculars from B to the arms of `angleA` show that:
BP=BQ or B is equidistant from the arms of `angleA`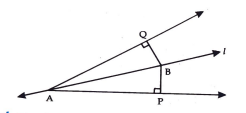 01:59View Solution
01:59View SolutionIn Fig.
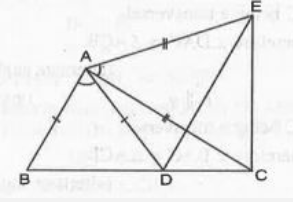
AC = AE, AB = AD and `angleBAD = angleEAC`. Show that BC = DE.03:29View SolutionAB is a line segment and P is its midpoint. D and E are points on the same side of AB such that `angleBAD = angleABE` and `angleEPA = angleDPB`. Show that AD=BE.
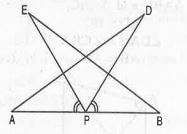 04:57View Solution
04:57View SolutionAB is a line segment and P is its midpoint. D and E are points on the same side of AB such that `angleBAD = angleABE` and `angleEPA = angleDPB`. Show that AD=BE.
 04:57View Solution
04:57View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.)

Show that : `CM=1/2AB`.06:00View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.)

Show that : `CM=1/2AB`.06:00View SolutionIn right triangle ABC, right angled at C, M is the mid point of hypotenuse AB. C is joined to M and produced to a point D such that DM=CM. point D is joined to point B. show that
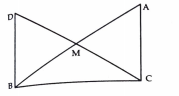
`triangleDBCequivtriangleACB`05:30View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.)

Show that : `CM=1/2AB`.06:00View SolutionIn an isosclees triangle ABC, with AB = AC, the bisectors of `angleB` and `angleC` intersect each other at O. Join A to O show that : OB=OC.
03:22View SolutionIn an isosclees triangle ABC, with AB = AC, the bisectors of `angleB` and `angleC` intersect each other at O. Join A to O show that : AO bisects `angleA`.
05:43View SolutionIn `triangleABC`, AD is the perpendicular bisector of BC. Show that `triangleABC` is an isosceles triangle in which AB=AC
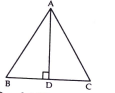 01:57View Solution
01:57View SolutionABC is an isosceles triangle in which altitudes BE and CF are drawn to sides AC and AB respectively (See Fig.
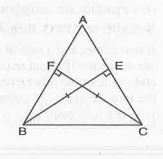 ). Show that these altitudes are equal.04:05View Solution
). Show that these altitudes are equal.04:05View SolutionABC is a triangle in which altitudes BE and CF are equal that:
`triangleABEequivtriangleACF` 03:40View Solution
03:40View SolutionABC is a triangle in which altitudes BE and CF on sides AC and AB are equal that:
ABAC, i.e.`triangleABC` is na isosceles triangle.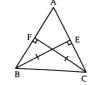 01:50View Solution
01:50View SolutionABC and DBC are two isosceles triangles are same base BC. Show that `angleABD=angleACD`
 02:22View Solution
02:22View Solution`DeltaABC` is an isoscelestriangle in which AB = AC. Side BA is produced to D such that AD = AB. Show that `angleBCD` is a right angle (see Fig.
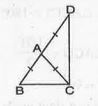 ).06:15View Solution
).06:15View SolutionABC is a right angled triangle in which `angleA = 90^@` and AB = AC. Find `angleB` and `angleC`.
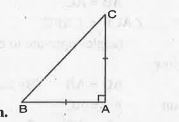 03:24View Solution
03:24View SolutionShow that the angles of are equilateral triangle are `60^@` each.
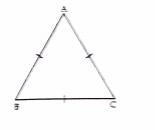 01:45View Solution
01:45View Solution`DeltaABC` and `DeltaDBC` are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
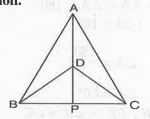 ).If AD is extended to intersect BC at P, show that `DeltaABD ~= DeltaACD`.03:17View Solution
).If AD is extended to intersect BC at P, show that `DeltaABD ~= DeltaACD`.03:17View Solution`DeltaABC` and `DeltaDBC` are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
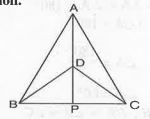 ).If AD is extended to intersect BC at P, show that `DeltaABP ~= DeltaACP`.05:54View Solution
).If AD is extended to intersect BC at P, show that `DeltaABP ~= DeltaACP`.05:54View Solution`DeltaABC` and `DeltaDBC` are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
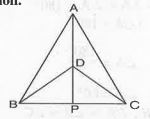 ).If AD is extended to intersect BC at P, show that AP bisects `angleA` as well as `angleD`.08:09View Solution
).If AD is extended to intersect BC at P, show that AP bisects `angleA` as well as `angleD`.08:09View Solution`DeltaABC` and `DeltaDBC` are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
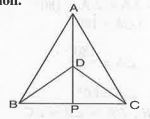 ).If AD is extended to intersect BC at P, show that AP is the perpendicular bisector of BC.07:51View Solution
).If AD is extended to intersect BC at P, show that AP is the perpendicular bisector of BC.07:51View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that AD bisects BC.
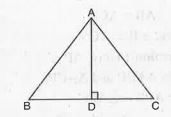 02:57View Solution
02:57View SolutionAD is an altitude of an isosceles triangle ABCD which AB=AC. Show that

AD bisects `angleA`03:39View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of `DeltaPQR` (See Fig
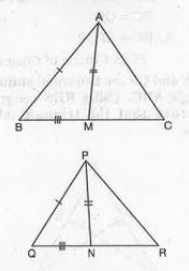 ). Show that : `DeltaABM ~= DeltaPQN`.05:05View Solution
). Show that : `DeltaABM ~= DeltaPQN`.05:05View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR are median PN of `trianglePQR`. Show that
`triangleABCequivtrianglePQR` 02:24View Solution
02:24View SolutionBE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
 04:25View Solution
04:25View SolutionABC is an isosceles triangle with AB=AC draw `APbotBC` to show that `angleB=angleC`
 02:41View Solution
02:41View SolutionShow that in a right angled triangle, the hypotenuse is the longest side.
06:53View SolutionIn Fig.
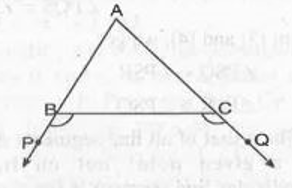 , sides AB and AC of `DeltaABC` are extended to points P and Q respectively. Also `anglePBC < angleQCB`. Show that `AC > AB`.04:04View Solution
, sides AB and AC of `DeltaABC` are extended to points P and Q respectively. Also `anglePBC < angleQCB`. Show that `AC > AB`.04:04View SolutionIn Fig.
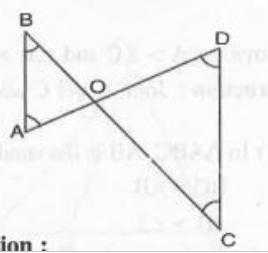 , `angleB < angleA` and `angleC < angleD`. Show that `AD < BC`.03:57View Solution
, `angleB < angleA` and `angleC < angleD`. Show that `AD < BC`.03:57View SolutionAB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see Fig. 7.50). Show that `angle A > angle C` and `angle B > angle D`.
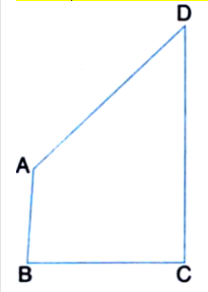 06:33View Solution
06:33View SolutionIn fig. PR>PQ and PS bisects `angleQPR`. Prove that `anglePSR>anglePSQ`
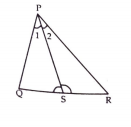 02:08View Solution
02:08View SolutionShow that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
07:14View SolutionABC is a triangle. Locate a point in the interior of `DeltaABC` which is equidistant from all the vertices of `DeltaABC`.
05:19View SolutionIn a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
05:06View SolutionIn a huge park, people are concentrated at the points
A: where there are difference slides for children
B: near which a man-made lake is situated
C: which is near to a large parking and each where should an icecream parlour be set up that maximum number of persons can approach it 02:51View Solution
02:51View SolutionComplete the hexagonal rangoli and the star Rangolies (see Figs.
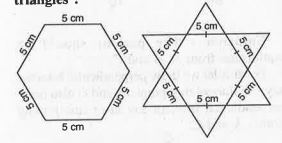 ) by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles ?02:10View Solution
) by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles ?02:10View SolutionIn trianlges ABC and PQR, `angleA=angleQ` and `angleB=angleR` which side of `trianglePQR` should be equal to side AB of `triangleABC` so that the two trianles are congruent? Give reasons for your answer.
01:40View SolutionIf .... sides(s) of a triangle is/are equal to the three sides of other triangle the two triangles are congruent.
01:52View SolutionIf .... And the included angle of one triangle are equal to two sides and the included angle of the other triangle then two triangles are congruent.
01:40View SolutionIf .... sides(s) of a triangle is/are equal to the three sides of other triangle the two triangles are congruent.
01:52View SolutionIs it possible to construct a triangle with length of its sides as 4 cm, 3 cm and 7 cm give reasons for your answer.
02:16View SolutionBy applying ASA congruence rule, it is to be established that `triangleABC ~= triangleQRP` and it is given that BC = RP. What additional information is needed to establish the congruence?
03:19View SolutionIf `trianglePQRequivtriangleEDF`, then is it true to say the PR=Ef? Give reason for your answer.
01:43View SolutionIn `trianglePQR`, `angleP=70^@` and `angleR=30^@` which side of this triangle is the longest? Give reason for your answer.
02:07View Solution
EXAMPLE questions and complete solutions for chapter TRIANGLES of MODERN PUBLICATION of Class 9
