Complete Solutions to EXERCISE of chapter CIRCLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | CIRCLES |
| MODERN PUBLICATION | EXERCISE |
| Number Of Questions | 94 |
| Academic Year | 2023-24 |
The radius of a circle is 8 cm and the length of its chords is 12 cm. Fid the distance of the from the centre.
View SolutionFind the length of a chord which is at a distance of 24 cm from the centre of a circle whose diameter is 50 cm.
View SolutionA chord of length 16 cm is drawn in a circle of radius 10 cm. Find the distance of the chord from the of the circle.
View SolutionFind the length of a chord which is at a distance of 24 cm from the centre of a circle whose diameter is 50 cm.
View SolutionPQ and RS are two parallel chords of a circle whose centre is O and radius is 10 cm. If PQ = 16 cm and RS = 12 cm, find the distance between PQ and RS, if they lie on the same side of the centre O.
View SolutionPQ and RS are two parallel chords of a circle whose centre is O and radius is 10 cm. If PQ = 16 cm and RS = 12 cm, find the distance between PQ and RS, if they lie on the opposite side of the centre O.
View SolutionAB and CD are two chords of a circle such that AB = 6 cm, CD = 12 cm and AB is parallel to CD. The distance between AB and CD is 3 cm. Find the radius of the circle.
View SolutionTwo parallel chords of lengths 30 cm and 16 cm are drawn on the opposite sides of the centre of a circle of radius 17 cm. find the distance between the chords.
View SolutionIn an equilateral triangle, prove that centroid and circumcentre coincide.
View SolutionTwo chords PQ and RS of a circle are parallel to each other and AB is the perpendicular bisector of PQ. Without using any construction, prove that AB bisects RS.
View SolutionIn fig., two circles with centres O, O' touch externally at a point A. A line through A is drawn to intersect these circles in B and C. Prove that the tangents at B and C are parallel.
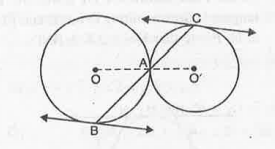
View SolutionProve that the right-bisector of a chord of a circle bisects the corresponding minor arc of the circle.
View SolutionTwo chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the angle bisector of `angleBAC`.
View SolutionTwo equal chords AB and CD of a circle C(O,r) when produced meet at a point E. Prove that:
BE = DE
View SolutionTwo equal chords AB and CD of a circle C(O,r) when produced meet at a point E. Prove that:
AE = CE
View SolutionIf a diameter of a cirlce bisects each of the chords of the circle, prove that the chordds are parallel.
View SolutionProve that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
View SolutionDiameter is the largest chord of the circle. (True/False)
View SolutionPQ and RQ are chords of a circle equidistant from the centre. Prove that the diameter passing through Q bisects `anglePQR`
View SolutionIn given Fig.
 , AD = AE and D and E are points on BC, such that BD = EC. Prove that AB = AC.
, AD = AE and D and E are points on BC, such that BD = EC. Prove that AB = AC.
View SolutionProve that of all chords of a circle through a given point within it, the least is one. Which is bisected at that point.
View SolutionBisector AD of `angleBAC of triangleABC` passes through the centre O of the circumcircle of `triangleABC` as shown in the figure Prove that AB = AC
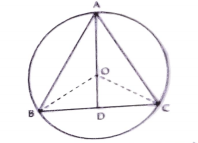
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chord.
View SolutionIf O is the centre of the circle, find the value of x in each of the following

View SolutionO is the centre of the circle and `angleAOB = 70^@`. Calculate the values of `angleOCA`
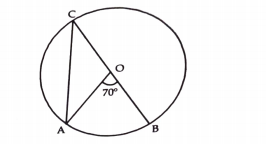
View SolutionO is the centre of the circle and `angleAOB = 70^@`. Calculate the values of `angleOAC`
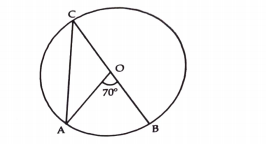
View SolutionO is the centre of the circle. If `angleABD = 35^@` and `angleBAC = 70^@`. Find `angleACB`
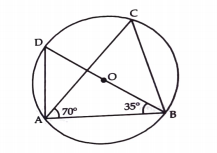
View Solution
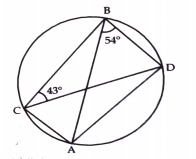 `angle ABD = 54^@ and angleBCD = 43^@`, calculate the `angleACD`
`angle ABD = 54^@ and angleBCD = 43^@`, calculate the `angleACD`
View Solution
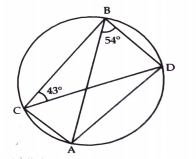 `angle ABD = 54^@ and angleBCD = 43^@`, calculate the `angleBAD`
`angle ABD = 54^@ and angleBCD = 43^@`, calculate the `angleBAD`
View Solution
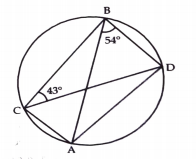 `angle ABD = 54^@ and angleBCD = 43^@`, calculate the `angleBDA`
`angle ABD = 54^@ and angleBCD = 43^@`, calculate the `angleBDA`
View SolutionDE is a chord parallel to diameter AC of the circle with centre O. If `angleCBD = 60^@`, calculate the `angleCDE`
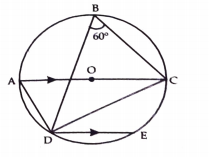
View SolutionC is a point on the minor arc of the circle, with centre O. If `angleACB = x^@` and express y in terms of x. Calculate x, if `ACBO` is a parallelogram.
View SolutionIf O is the circumcentre of a `triangleABC, OD bot BC`, prove that `angleBOD = angleA`
View SolutionTwo diameters of a circle intersect each other at right angles. Prove that the quadrilateral formed by joining their end points is a square.
View SolutionAB is a diameter of the circle C(AO,R) and the radius OD is perpendicular to AB. If C is any point on the arc DB, find `angleBAD and angleACD`

View SolutionProve that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the third side of the triangle.
View SolutionAC is the diamter of a circle with centre AO and chord `BD bot AC`, intersecting each other at E. Find the values p,q,r in terms of x.
View SolutionFill in the Blanks:
The centre of a cirlce lies in _____ of the cirlce. (exterior/interior)
View SolutionA point, whose distance from the centre of a circle is greater than its radius lies in .................. Of the circle.
View SolutionThe longest chord of a circle is a ........... of the circle.
View SolutionAn arc is a ........... When its ends are the ends of a diameter.
View SolutionSegment of a circle is the region between an arc and ........... of the circle.
View SolutionFill in the Blanks:
A circle divides the plane, on which it lies, in ______ parts.
View Solution(True/ False) Line segment joining the centre to any point on the circle is a radius of the circle.
View Solution(True/ False) A circle has only finite number of equal chords.
View Solution(True/ False) If a circle is divided into three equal arcs each is a major arc.
View Solution(True/ False) A chord, which is twice as long as its radius is a diameter of the circle.
View Solution(True/ False) Sector is the region between the chord and its corresponding arc.
View Solution(True/ False) A circle is a plane figure.
View SolutionName the region between a chord and either of the arcs.
View SolutionIf diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
View SolutionGiven three non-collinear points. How many circles can be drawn through these three points?
View SolutionIn a triangle with one angle `(2pi)/(3),` the lengths of the sides form an A.P. If the length of the greatest side is 7 cm, the radius of the circumcircle of the triangle is
View SolutionIn a circle C(O,r), AOB and COD are two diameters perpendicular to each other. Find length of chord AC.
View SolutionTwo congruent circles with centres C and O' intersect at A and B. If `angleAO'B = 50^@`, then find `angleACB`
View SolutionTrue/False:
The degree measure of a semi-circle is `180^@`
View Solution(True/ False) A circle has only finite number of equal chords.
View SolutionTrue/False:
The perimeter of circle is called its circumference .
View SolutionTrue/False:
A circle divides the plane into three parts.
View SolutionTrue/False:
Let O be the centre of a circle with radius r. Then a point P such that OP < r is called an interior point of the circle.
View SolutionTrue/False:
An equilateral triangle ABC is inscribed in a circle with centre O. The measure of `angleBOC` is `60^@`
View SolutionThe perpendicular from the centre of a circle to a chord bisects the chord.
View SolutionIn a circle C(O,r), AOB and COD are two diameters perpendicular to each other. Find length of chord AC.
View SolutionTrue/False:
The degree measure of a semi-circle is `180^@`
View SolutionTwo circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
View SolutionFill in the Blanks:
Angles in the same segment of a circle are ________
View SolutionFill in the Blanks:
Equal arcs of a circle subtend_____ angles at the centre.
View SolutionFill in the Blanks:
Angles subtended by an arc at the centre of a circle is _______ the angle subtended by the same arc at any other point on the remaining part of the circle.
View SolutionFill in the Blanks:
Equal chords of a cirlce (or congruent circles) are _______ from the centre.
View SolutionFill in the Blanks:
The line drawn through the centre of a circle to ______ a chord is perpendicular to the chord.
View SolutionFill in the Blanks:
Chords _____ from the centre of a circle are equal in length.
View SolutionFill in the Blanks:
The perpendicular from the centre of a circle to a chord _____ the chord.
View SolutionFill in the Blanks:
The sum of either pair of opposite angles of a ______ quadriateral is `180^@`
View SolutionThe longest chord of a circle is a ........... of the circle.
View SolutionAn arc is a ........... When its ends are the ends of a diameter.
View SolutionA chord is at a distance of 8 cm from the centre of a circle of radis 17 cm. The length of the chord is
View SolutionAn equilateral triangle of side 9 cm.
View SolutionIs every diameter of a circle also a chord?
View SolutionIf OA = 5 cm , AB = 8 cm and OD is perpendicular to AB, then OD is equal to
View Solution(True/ False) If AOB is a diameter of a circle and C is a point on the circle, then `AC^2 + BC^2 - AB^2`.
View SolutionABCd is a cyclic quadrialteral such that AB is a diameter of the circle circumscribing it and `angleADC = 140^@, then angleBAC` is equal to
View SolutionProve that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals.
View SolutionIf `angleABC= 20^@`m find `angleAOC`
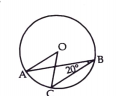
View Solution`angleDAB = 60^@, angleABD = 50^@` find `angleACB`

View SolutionIf arc AXB and CYD of a circle are congruent, find the ratio of AB and CD
View SolutionTwo triangles ABC and PQR are such that the perpendiculars from A to QR ,B to RP and C to PQ are concurrent .Show that the perpendicular from P to BC ,Q to CA and R to AB are also concurrent .
View SolutionIf a diameter of a cirlce bisects each of the chords of the circle, prove that the chordds are parallel.
View SolutionThe whole angle at the centre of a circle is :
View SolutionIn a triangle ABC, D is the mid point of the side AC and `BD=1/2AC`. Show that `angleABC` is a right angle.
View SolutionOn a common hypotenuse AB, two right triangles ACB and ADB are situated on opposite `angleBAC = angleBDC`
View SolutionIf the non-parallel sides of a trapezium are equal, prove that it is cyclic.
View SolutionIn fig, two chords AB and CD intersect each other at the point P. Prove that:
(i) `triangleAPC ~ triangleDPB`
(ii) AP.PB= CP.DP

View SolutionDraw a circle of radius 5 cm and divide it into 6 equal sectors .
View Solution
EXERCISE questions and complete solutions for chapter CIRCLES of MODERN PUBLICATION of Class 9