Complete Solutions to EXAMPLE of chapter CIRCLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | CIRCLES |
| MODERN PUBLICATION | EXAMPLE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The radius of a circle is 13 cm and the length of one of its chord is 10 cm. Find the distance of the chord from the centre.
View SolutionFind the length of a chord which is at a distance of 24 cm from the centre of a circle whose diameter is 50 cm.
View SolutionTwo circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
View SolutionIn the figure
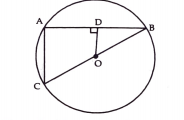 OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA = 2OD
OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA = 2OD
View SolutionTwo cocentric circle common centre O. A line 'l' intersects these circle A,B,C and D. Prove that AB = CD.
View SolutionTwo circles with centres O and O' intersect at P. Through P, a line 'l' parallel to a OO', meeting circles at C and D, is drawn. Prove that CD = 2OO'
View SolutionTwo chords PQ and RS of a circle are parallel to each other and AB is the perpendicular bisector of PQ. Without using any construction, prove that AB bisects RS.
View SolutionProve that the right-bisector of a chord of a circle bisects the corresponding minor arc of the circle.
View SolutionIf a diameter of a cirlce bisects each of the chords of the circle, prove that the chordds are parallel.
View SolutionIf two intersecting chords of a circle make equal angles with the diameter passing through their point of intersection, prove that the chords are equal.
View SolutionAB and CD are two chords of a circle such that AB = 6 cm, CD = 12 cm and AB is parallel to CD. The distance between AB and CD is 3 cm. Find the radius of the circle.
View SolutionProve that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
View SolutionIn the given figure
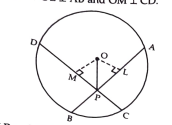 O is the centre of a circle and PO bisects `angleAPD`. Prove that AB = CD
O is the centre of a circle and PO bisects `angleAPD`. Prove that AB = CD
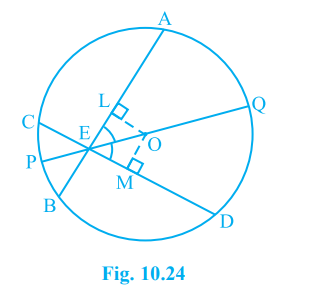
View SolutionL and M are mid-points of two eqal chords AB and CD of a circle with centre O Prove that
`angleOLM = angleOML`
View SolutionL and M are mid-points of two equal chords AB and CD of a circle with centre O Prove that
`angleALM = angleCML`
View SolutionTwo equal chords AB and CD of a circle with centre O, intersect each other at E. Prove that AD = CB
View SolutionEqual chords AB and CD of a circle with centre O, cut at right angles at E. If L and M are the mid-points of AB and CD respectively, prove that OLEM is a square.
View SolutionIf two chords of a circle bisect one another they must be diameters.
View SolutionOA and OB are respectively perpendicular to chors CD and EF of a circle whose centre is O. If OA = OB, prove that `CE congDF`

View SolutionIf O is the centre of a circle, find the value of x in each of the following figures
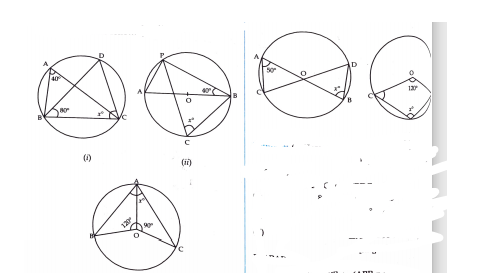
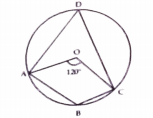
View SolutionO is the centre of the circle and the measure of arc AOC is `120^@`. Find `angleADC and angleABC`
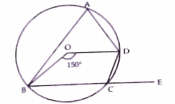
View SolutionO is the centre of the circle. The angle subtended by the ar BCD at the centre is `150^@`. BC is produced to E. Find `angleBAD and angleBCD`
View SolutionAB is a diameter of the circle C(AO,R) and the radius OD is perpendicular to AB. If C is any point on the arc DB, find `angleBAD and angleACD`

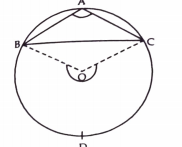
View SolutionO is the centre of the circle. Prove that `anglex + angley = anglez`
View SolutionAB = CD. Prove that BE = and AE = Ce, where E is the point of intersection AD and BC.

View SolutionABC and ADC are two right triangles with common hypotenuse AC. Prove that `/_CAD = `/_CBD`.
View SolutionIf O is the circumcentre of a `triangleABC, OD bot BC`, prove that `angleBOD = angleA`
View SolutionProve that the angle in a segment smaller than a semi-cricle is greater than a right angle.
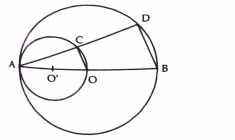
View SolutionAB is a diameter of a circle having centre O and a circle is described having AO as diameter. A chord AD of the bigger circle intersects the smaller circle at C. Prove that BD = 2OC.
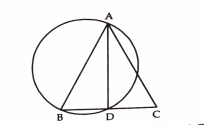
View SolutionProve that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
View SolutionIn the figure
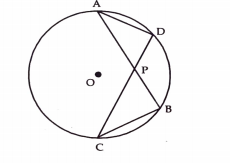 AB and CD are two chords of a circle, intersecting each other at P such that AP = CP show thawt AB = CD.
AB and CD are two chords of a circle, intersecting each other at P such that AP = CP show thawt AB = CD.
View SolutionProve that in a right angled triangle the mid-point of the hypotenuse is equidistant from its vertices.
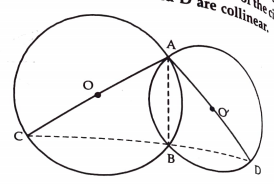
View SolutionTwo circles intersect at A and and AC,AD are respectively the diameter of the circle . Prove that the points C,B and D are collinear.
View SolutionABCD is a cyclic quadrilateral in which AC and BD are its diagonals.If `angleDBC = 70^@ and angle BAC = 30^@` find `angleBCD`
View SolutionABCD is a cyclic quadrialteral O is the centre of the circle. If `angleBOD = 160^@`, find `angleBPD`
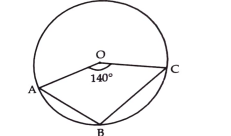
View SolutionO is the4 centre of the circle. If `angleAOC = 140^@`. Find `angle ABC`
View SolutionIf O is the centre of the circle, `angleAOC = 110^@` and side AB is produced to D, find `angleCBD`
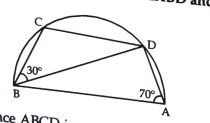
View SolutionC and D are the points on the semi-circle described on BA as diameter. Given `angleBAD = 70^@ and angleDBC = 30^@`. Find `angleABD and angleBDC`
View SolutionA,B,C and D,E,f are two of collinear points. Prove that AD||CF
View SolutionABC is an isosceles triangle in which AB = AC. If D and E are the mid-points of AB and respectively, prove that B,C,D and E are concyclic.
View SolutionAOB is a diameter of the circle withi centre O. Find the numerical value of `angleACD + angleDEB`
View SolutionABCD is a cyclic quadrilateral. A circle passing through A and B meets AD and BC in E and F respectively. Prove that EF||DC
View SolutionAB and CD are two parallel chords of a circle and lines CA and DB intersect each other at O. Show that OA = OB.
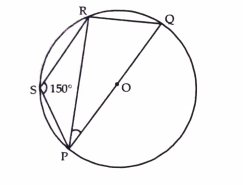
View SolutionPOQ is a diameter and PQRS is a cyclic quadrilateral. If `anglePSR = 150^@`, find `angleRPQ`
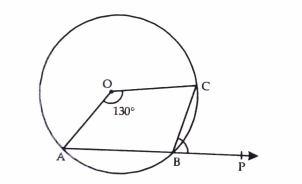
View SolutionO is the centre of the circle and arc ABC subtends an angle of `130^@` at the centre. If AB is extended to P, find `anglePBC`
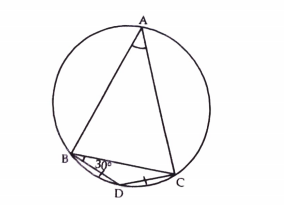
View SolutionBD = DC and `angleCBD = 30^@`, find `mangleBAC`
View Solution`triangleABC` is an equilateral triangle `angle BEC`

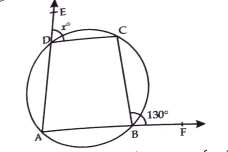
View SolutionSides AD and AB of cyclic quadrilateral ABCD are produced to E and F respectively. If `angleCBF = 130^@` and `angleCDE = x^@`, find the value of x.
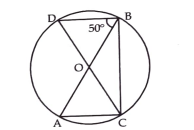
View SolutionAB and CD are diameters of a circle with centre O. If `angle OBD = 50^@`, find `angleAOC`
View SolutionO is the4 centre of the circle. If `angleAOC = 140^@`. Find `angle ABC`

View SolutionO is the centre of a circle. If `angleAOD = 140^@` and `angleCAB = 50^@`, calculate the `angleEBD`
View SolutionProve that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals.
View SolutionChords AB and Cd of a circle are produced to meet at E. Prove that `triangleEDB and triangleEAC` are similar.
View SolutionProve that the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diaognsls.
View SolutionProve that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals.
View SolutionABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = Ed. Prove that AD ||BC
View SolutionABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = Ed. Prove that EB = EC
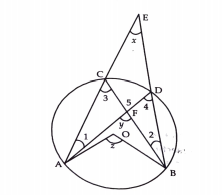
View SolutionP and Q are centres of two circles, intersecting at B and C, and ACD is a striaght line.
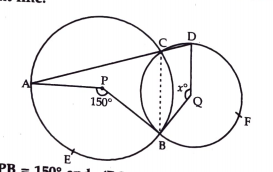 If `angleAPB = 150^@` and `angleBQD = x^@`, find the value of x.
If `angleAPB = 150^@` and `angleBQD = x^@`, find the value of x.
View SolutionProve that any four vertices of a regular pantagon are concyclic.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chord.
View SolutionThe bisector of `angleB` of an isosceles triangle `triangleABC` with AB = AC meets the circumcircle of `triangleABC` at P as shown in the figure. If AP and BC produced meet at Q, prove that CQ = CA.
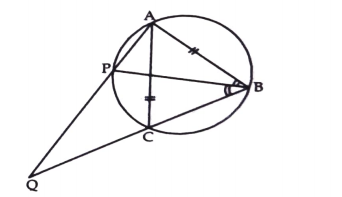
View SolutionABC is a triangle in which `angleBAc = 30^@`. Prove that BC is the radius of the circumcircle of `triangleABC`, whose centre O.

View SolutionThree STd booths situated at P,Q and R is the fiure are operated by handicaped ersons. These three booths are equidistant from each other
 Find `angleQPR`
Find `angleQPR`
View SolutionRecall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
View SolutionProve that if chords of congruent circlessubtend equal angles at their centres, then the chords are equal.
View SolutionDraw different pairs of circles. How many points does each pair have in common ? What is the maximum number of common points ?
View SolutionSuppose you are given a circle. Give a construction to find its centre.
View SolutionIf two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
View SolutionTwo circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chord.
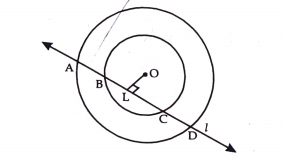
View SolutionIf a line intersects two concentric circles (circles with the same centre) with centre O at A,B,C and D, prove that AB = CD
View SolutionA circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
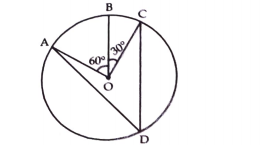
View SolutionA,B and C are three points on a circle with centre AO such that `angleBOC = 30^@, angleAOB = 60^@`. If D is a point on the circle other than the are ABC, find `angleADC`
View SolutionA chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord on a point on the minor arc and also at a point on the major arc.
View SolutionIn the given figure, `angle PQR = 100^@`, where P, Q and R are points on a circle with centre O. Find `angle OPR`.
View SolutionIn Fig. 10.38, `angle ABC = 69^@`, `angle ACB = 31^@`, find `angle BDC`.
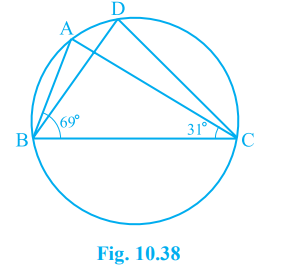
View SolutionABCD is a cyclic quadrilateral whose diagonals intersect at a point E. `/_DBC = 70^@`, `/_BAC is 30^@`, find `/_BCD`. Futher, if AB = BC, find `/_ECD`.
View SolutionIf diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
View SolutionIf the non-parallel sides of a trapezium are equal, prove that it is cyclic.
View SolutionIf circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
View SolutionABC and ADC are two right triangles with common hypotenuse AC. Prove that `/_CAD = `/_CBD`.
View SolutionProve that a cyclic parallelogram is a rectangle.
View SolutionProve that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
View SolutionTwo chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
View SolutionThe lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at a distance of 4 cm from the centre, what is the distance of the other chord from the centre ?
View SolutionLet vertex of an angle ABC be located outside a circle and let the sides of the angle intersect chords AD and CE with the circle. Prove that `/_ABC` is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
View SolutionProve that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals.
View SolutionABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
View SolutionAC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters, (ii) ABCD is a rectangle.
View SolutionAC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters, (ii) ABCD is a rectangle.
View SolutionBisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that angles of the triangle are `90^@-A/2,90^@-B/2` and `90^@-C/2` respectively.
View SolutionTwo congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
View SolutionIn any triangle ABC, if the angle bisector of `/_A` and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
View Solution(True/ False) Two chords AB and CD of a circle are each at distances 4 cm from the centre. Then AB = CD.
View SolutionTwo chords AB and AC of a circle with centre O are on the opposite sides of OA. Then `angleOAB = angleOAC`
View Solution(True/ False) Two congruent circles with centres O and O' intersect at two points A and B. Then `/_AOB = /_AO'B`.
View SolutionThrough three collinear points a circle can be drawn.
View Solution(True/ False) A circle of radius 3 cm can be drawn through two points A, B such that AB = 6 cm.
View Solution
EXAMPLE questions and complete solutions for chapter CIRCLES of MODERN PUBLICATION of Class 9