Complete Solutions to Solved Examples of chapter SURFACE AREA AND VOLUME of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | SURFACE AREA AND VOLUME |
| NAGEEN PRAKASHAN | Solved Examples |
| Number Of Questions | 63 |
| Academic Year | 2023-24 |
Find the volume and total surface area of a cuboid, whose length = 15 cm, breadth = 10 cm and height = 8 cm.
View SolutionThe total surface area of a cube is `294 cm^(2)`, find its volume.
View SolutionThe length, breadth and height of a cuboid are in the ratio 6 : 5 : 3. If its total surface area is `504 cm^(2)`, find its dimensions. Also find the volume of the cuboid.
View SolutionThree equal cubes are placed adjacently in a row. Find the ratio of total surface area of the new cuboid to that of the sum of the surface areas of the three cubes.
View SolutionFind the volume of wood required for a closed wooden box with external dimensions `15cm xx 12cmxx8cm`, if the wood is `0.5 cm` thick.
View SolutionThe length, breadth and height of a room are `9 m, 7 m` and `4 m` respectively. There are two doors measuring `2m xx 1.5 m` and four windows measuring `1.5m xx 1m`. Find the area doors remaining walls.
View SolutionThe length, breadth and height of a room are 5 m, 4 m and 3 m respectively. Find the cost of white washing the walls of the room and the ceiling at the rate of `R s\ 7. 50\ p e r\ m^2dot`
View SolutionShanti sweets stall was placing an order for making cardboard boxes for packing their sweets. Two sizes of boxes were required. The bigger of dimensions `25cm xx 20cm xx 5 cm` and the smaller of dimensions `15cm xx 12cm xx 5cm`. For all the overlaps, `5%` of the total surface area is required for supplying `250` boxes of each kind.
View SolutionIn a box whose dimensions are `12cm xx 4cm xx 3cm`, how long stick can be placed ?
View SolutionWater flows in a tank `150 mx100m` at the base, through a pipe whose cross-section is `3d m` by `1. 5 d m` at the speed of `15 km per hour dot` In what time, will the water be `3m e t r e s` deep?
View SolutionA godown measures `40\ m\ xx\ 25\ m\ xx\ 10\ m`. Find the maximum number of wooden crates each measuring `1. 5\ m\ xx\ 1. 25\ m\ xx\ 0. 5\ m`that can be stored in the godown.
View SolutionThe sum of length, breadth and depth of a cuboid is 12 cm and its diagonal is `5sqrt(2)` cm. Find its surface area.
View SolutionThe circumference of the base of a cylinder is 130 cm andheight is 20 cm. Find its curved surface area.
View SolutionFind the curved surface area of the cylinder whose height is 20 cm and the radius of base is 7 cm.
View SolutionThe area of the base of a right circular cylinder is `42pi cm^(2)` and height is 3.5 cm. Find its volume.
View SolutionThe height and radius of the base of a right circular cylinder is 'r'. Find its totalsurface area.
View SolutionThe side of a paper of square shape is 44 cm. It is folding and convert into a cylinder. Find the curved surface area and total surface of the cylinder.
View SolutionThe radius of base of a cylinder is 7 cm and height is 10 cm. Find its curved surface area and volume.
View SolutionThe area of base of a cylinder is `616 cm^(2)` and height is 30 cm. Find its volume and total surface area.
View SolutionThe volume of a cylindrical tub is `6160 m^(3)`. If the diameter of its base is 28 m, then find its depth.
View SolutionThe curved surface of a right circular is `4400 cm^(2)` and height is `50 cm.` Find its volume and total surface area.
View SolutionThe total surface area of a cylinder is `1540 cm^(2)`. The height of cylinder is 4 times the radius of the base. Find the height of the cylinder.
View SolutionThe radius and height of a cylinder are in the ratio 5 : 7 and its volume if `550\ c m^3dot` Find its radius. `(U s e\ pi=(22)/7)`
View SolutionThe radius of right circular cylinder is 14 cm. If its total surface area is `3872 cm^(2)`, then find its height.
View SolutionA cylinder is formed by folding a square of side 5 cm. Find its curved surface area and the volume.
View SolutionA rectangular paper of `22cm xx 12cm` is folded in two different ways and formed two cylinders.
(i) Find the ratio of the volumes of two cylinders.
(ii) Find the difference of the volumes of two cylinders.
View SolutionThe volume of a cylindrical vessel is `27720 cm^(3)`. Itscurved surface is `2640 cm^(2)`. Find its height and radius of base.
View SolutionThe diameter of a roller is `84 cm` and its length is `120 cm.` It takes `500` complete revolutions to move once over to level a playground. Find the area of the playground in `m^2`.
View SolutionThere is some water in a cylindrical vessel of diameter `11 cm` . A solid cube of side `5.5 cm` is dropped into the water , which immersed completely in the water . Find the increase in the height of surface of water in the vessel.
View SolutionThe rain water from a roof af dimensions ` 22 m xx 20 m ` drains into a cylindrical vessel having diameter of bases `2 m` and height `3.5 m.` If the rain water collected form the roof just fill the cylindrical vessel, them find the rainfall (in cm).
View SolutionThe diameter of a right circular cylinder is increased by 20%. Find the percentage decrease in its height if its volume remains unchanged.
View SolutionA cylindrical well of radius 4m and depth 49 m is dug and the taken out is spread evenly on a ground of length40 m and breadth 28 m. If the volume of the earth taken out increases by 10%, find the increase in the height of the ground.
View SolutionThe external and internal radii of a hollow cylinder are 5 cm and 4 cm respectively. If the height of cylinder is 14 cm, then find its internal volume and total surface area.
View SolutionThe radius and height of a right circular cone are 4 cm and 9 cm respectively. Its volume will be :
(i) `36pi cm^(3)` (ii) `48pi cm^(3)` (iii) `72pi cm^(3)` (iv) `100pi cm^(3)`
View SolutionThe ratio of the slant height and radius of the cone is 7 : 4. If itscurved surface area is `550 cm^(2)`, then find its radius.
View Solution`264m^(2)` cloth is used in a conical tent. If its slant height is 12 m, then find its height.
View SolutionThe volume of a right circular cone is `9702 cm^(3)` andheightis 21 cm. Find its curved surface area.
View SolutionFive persons can accommodate in a conical tent. If each person required `18` square decimetre place on wrath and `108` cubic decimetre air for breathing, then find the height of the cone.
View SolutionThe slant height of a cone is `13 cm` and its total surface area is `90pi cm^(2)`. Find its radius of base.
View SolutionThe height and radius of a right circular cone are increased by `20%` and `25%` respectively. Find the ratio of the volume of new cone and old cone.
View SolutionIn a right angle, the sides conrtaining right angles are 5 cm and 12 cm. It is rotated aboutits hypotenuse taking it as axis. Find the total surface area and volume of formed figure.
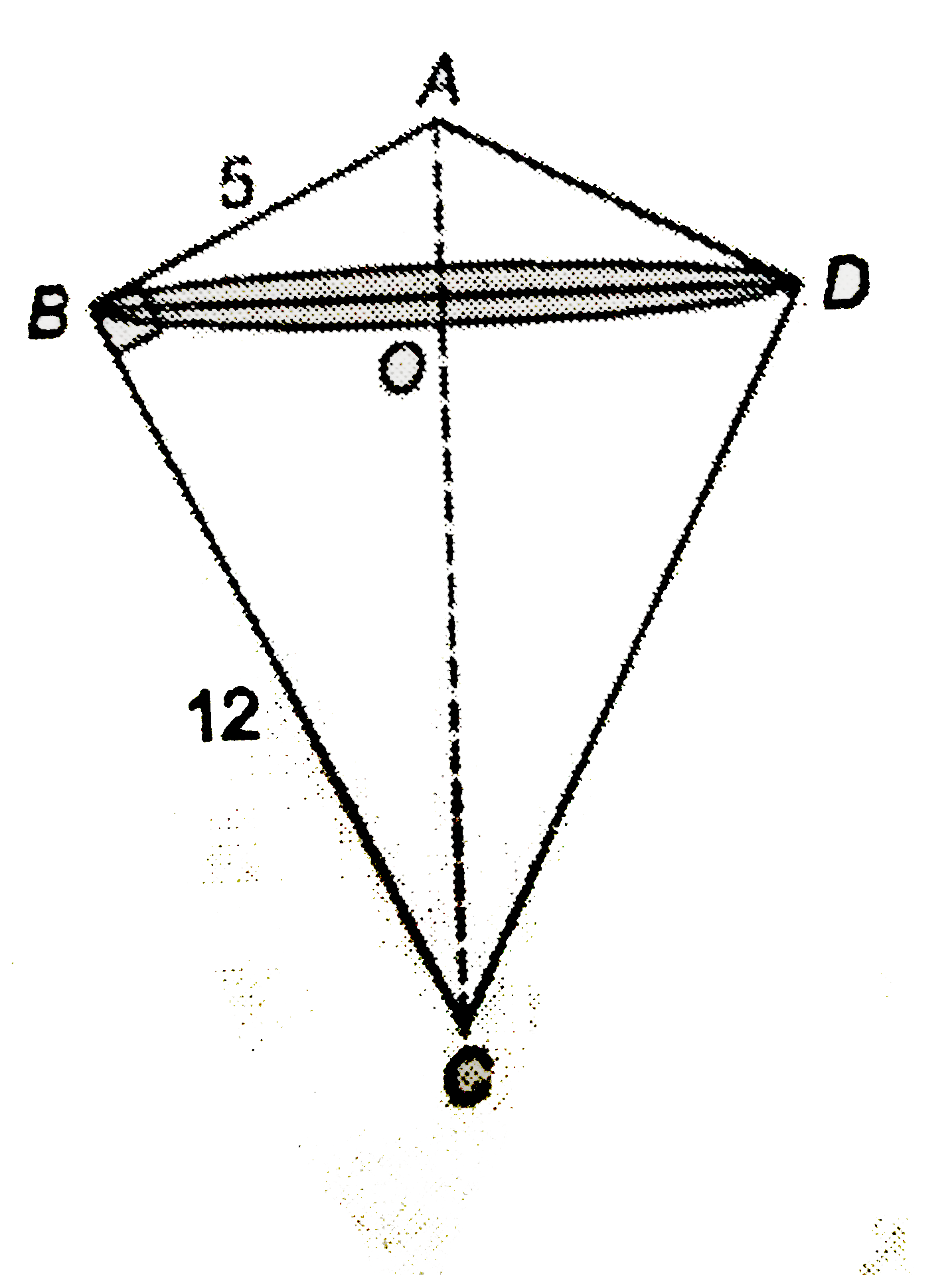
View SolutionAn open conical cup is formed from a thin metallic semi-circular sheet of diameter 28 cm. Find its volume.
View SolutionA conical tent is required to accommodate157 persons, each person must have `2 m^(2)` of space on the ground and `15 m^(3)` of air to breath. Find the height of the tent, also calculate the slant height.
View SolutionThe curved surface area of a cone of height 8 m is `188.4 m^(2)`. Find the volume of cone.
View SolutionIf `h , c ,V` are respectively the height, the curved surface and the volume of a cone, prove that `3piV h^3-C^2h^2+9V^2=0.`
View SolutionFind the length of canvas, 1.5m in width, is required to make a conical tent 14 m in diameter and 24 m in height. Given that `8(1)/(3)%` of the canvas is used in folds and stiching. Also, find the cost of canvas at the rate of Rs. 28 per metre.
View SolutionThe radius of a sphere is 3 cm. Its total surface area will be :
(1) `18pi cm^(2)` (ii) `36 pi cm^(2)` (iii) `72pi cm^(2)` (iv) `108 pi cm^(2)`
View SolutionFind the volume and curved surface of a sphere whose diameter is 6 cm.
View SolutionFind the volume of a spherewhose diameter is 1 cm.
View SolutionFind the total surface area of a hemisphere whose radius is 1 cm.
View SolutionThe diameter of a sphere is 10 cm. Find its surface area.
View SolutionThe surface area of a sphere is `100pi cm^(2)` . Find its volume.
View SolutionIf volumes of two spheres are in the ratio 64:27 then the ratio of their surface areas is
View SolutionThe diameter and height of a right circular cylinder are equal to the diameter of a sphere. Find the ratio of volumes of cylinder and sphere.
View SolutionFind the ratio of the surface of a sphere and total surface area of a hemisphere.
View SolutionA semi-circle of radius 17.5 cm is rotated about its diameter. Find the curved surface of so generated solid.
View SolutionFind the cost of painting at the rate of `Rs. 5.60 per m^(2)` on the hemispherical dome of diameter 10 m.
View SolutionThe sphere and cube have same surface. Show that the ratio of the volume of sphere to that of cube is `root`6 : `root``pi`
View SolutionThe diameters of three solid balls of iron are 6 cm, 8 cm and 10 cm. They are melted and recast a solid ball. Find the diameter of this ball.
View SolutionHow many balls, each of radius 1 cm, can be made from a solid sphere of lead of radius 8 cm?
View SolutionA sphere and a cube has same surface area.Show that the ratio of the volume of sphere to cube is `sqrt6:sqrtpi`
View SolutionA conical vessel of radius 6 cm and height 8 cm is completely filled with water. a sphere is lowered into the water and its size is such that when it touches the the sides, it just immersed. what fraction of water overflows.
View SolutionThe diagram shows the cross-section of eight identical iron balls touching each other on a horizontal surface.

If the volume of a ball is `(9pi)/(2)cm^(3)`, then what should be the minimum length and depth of a box so that all the balls can be placed in it ?
View Solution
Solved Examples questions and complete solutions for chapter SURFACE AREA AND VOLUME of NAGEEN MATHS (HINGLISH) of Class 9