Complete Solutions to LONG ANSWER TYPE QUESTIONS of chapter QUADRILATERALS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | QUADRILATERALS |
| NCERT EXEMPLAR | LONG ANSWER TYPE QUESTIONS |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
A square is incribed in an isoceles right triangle, so that the square and the triangle have one angle common. Show that the vertex of the sqare opposite the vertex of the common angle bisects the hypotenuse.
View SolutionIn a parallelogram ABCD, AB = 10 cm and AD = 6 cm. The bisector of `angleA` meets DC in E. AE and BC produced meet at F. Find the length of CF.
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View SolutionABCD is a rhombus and P, Q, R and S are wthe mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
View SolutionP, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC=BD and `ACbotBD`. Prove that PQRS is a square.
View SolutionIf diagonal of a parallelogram bisects one of the angles of the parallelogram, it also bisects the second angle.
View SolutionABCD is a parallelogram in which P and Q are mid-points of opposite sides AB and CD (see Fig. 8.18). If AQ intersects DP at S and BQ intersects CP at R, show that: (i) APCQ is a parallelogram. (ii) DPBQ is a parallelogram.
View SolutionABCD is a quadrilateral in which AB||DC and AD = BC. Prove that `angleA=angleB and angleC= angleD`.
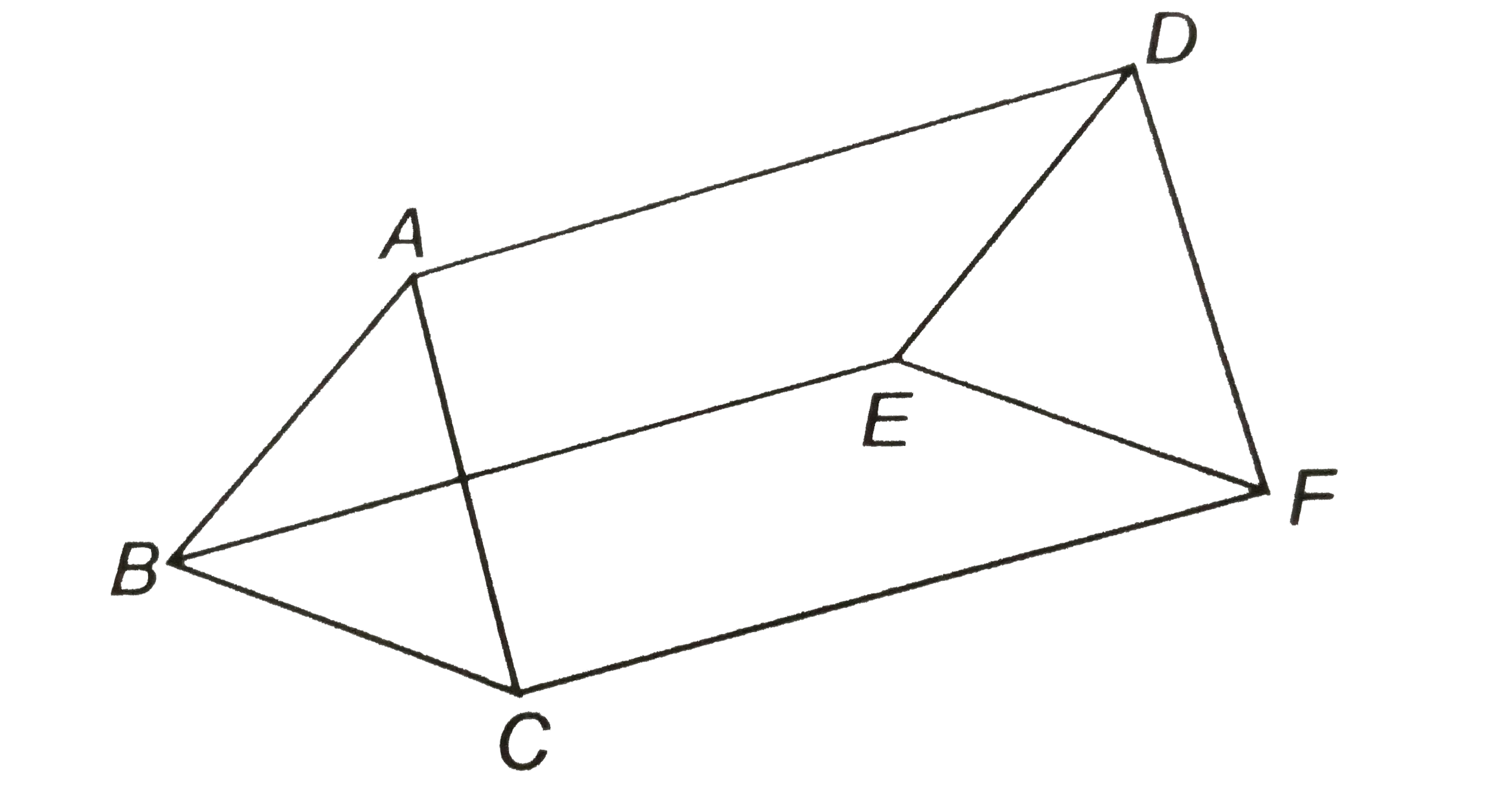
View SolutionIn figure, AB||DE, AB=DE, AC||DF and AC=DF. Prove that BC||EF and BC=EF.
View SolutionIn ` A B C ,A D` is the median through `A` and `E` is the mid-point of `A D` . `B E` produced meets `A C` in `F` (Figure). Prove that `A F=1/3A Cdot`
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square, is also a square.
View SolutionIn Figure, `A B C D` isa trapezium in which side `A B` is a parallel to side `D C` and `E` is the mid-point of side `A Ddot` If `F` is a point on the side `B C` such that the segment `E F` is parallel to side `D C` . Prove that `F` is the mid point of `B C` and `E F=1/2(A B+D C)dot`
View SolutionProve that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.

View SolutionP and Q are points on opposite sides AD and BC of a parallelogram ABCD such that PQ passes through the point of intersection O of its diagonals AC and BD. Show that PQ is bisected at O.
View SolutionABCD is a rectangle in which diagonal BD bisects `angle B`. Show that ABCD is a square.
View SolutionIn `DeltaA B C`, D, E and F are respectively the mid-points of sides AB, BC and CA. Show that `DeltaA B C`is divided into four congruent triangles by joining D, E and F.
View SolutionProve that the line segment joining the mid-points of the diagonals of a trapezium is parallel to each of the parallel sides and is equal to half the difference of these sides.
View SolutionP is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.
View Solution
LONG ANSWER TYPE QUESTIONS questions and complete solutions for chapter QUADRILATERALS of NCERT MATHS (ENGLISH) of Class 9