P and Q are points on opposite sides AD and BC of a parallelogram ABCD such that PQ passes through the point of intersection O of its diagonals AC and BD. Show that PQ is bisected at O.
To show that line segment PQ is bisected at point O, we will use the properties of triangles and congruence.
1. Draw the Parallelogram and Points:
- Start by drawing parallelogram ABCD. Label the points A, B, C, and D in a clockwise manner.
- Mark points P and Q on sides AD and BC respectively, such that line segment PQ passes through point O, the intersection of diagonals AC and BD.
2. Identify Properties of the Parallelogram:
- Recall that in a parallelogram, the diagonals bisect each other. Therefore, we have:
OD=OB
- This means that the lengths of segments OD and OB are equal.
3. Analyze Angles in Triangles:
- Consider triangles ODP and OBQ.
- Note that:
- Angle ∠ODP (let's call it angle 1) is equal to angle ∠OBQ (let's call it angle 2) because they are vertically opposite angles.
- Also, angle ∠POD (let's call it angle 3) is equal to angle ∠QOB (let's call it angle 4) because they are alternate interior angles (since AD is parallel to BC).
4. Establish Congruence of Triangles:
- Now we have:
- OD=OB (from the property of the parallelogram)
- Angle 1 = Angle 2 (vertically opposite angles)
- Angle 3 = Angle 4 (alternate interior angles)
- By the AAS (Angle-Angle-Side) criterion, we can conclude that:
△ODP≅△OBQ
5. Apply Corresponding Parts of Congruent Triangles (CPCT):
- Since the triangles ODP and OBQ are congruent, it follows that their corresponding sides are equal. Thus:
OP=OQ
6. Conclusion:
- Since OP = OQ, we conclude that line segment PQ is bisected at point O.
- Start by drawing parallelogram ABCD. Label the points A, B, C, and D in a clockwise manner.
- Mark points P and Q on sides AD and BC respectively, such that line segment PQ passes through point O, the intersection of diagonals AC and BD.
- Recall that in a parallelogram, the diagonals bisect each other. Therefore, we have:
OD=OB
- This means that the lengths of segments OD and OB are equal.
- Consider triangles ODP and OBQ.
- Note that:
- Angle ∠ODP (let's call it angle 1) is equal to angle ∠OBQ (let's call it angle 2) because they are vertically opposite angles.
- Also, angle ∠POD (let's call it angle 3) is equal to angle ∠QOB (let's call it angle 4) because they are alternate interior angles (since AD is parallel to BC).
- Now we have:
- OD=OB (from the property of the parallelogram)
- Angle 1 = Angle 2 (vertically opposite angles)
- Angle 3 = Angle 4 (alternate interior angles)
- By the AAS (Angle-Angle-Side) criterion, we can conclude that:
△ODP≅△OBQ
- Since the triangles ODP and OBQ are congruent, it follows that their corresponding sides are equal. Thus:
OP=OQ
- Since OP = OQ, we conclude that line segment PQ is bisected at point O.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - QUADRILATERALS EXERCISE - SHORT ANSWER TYPE QUESTIONS10videos
QUADRILATERALS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - POLYNOMIALSEXERCISE - EXERCISE 2.4 Long Answer type Questions9videos
POLYNOMIALS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS12videos
STATISTICS AND PROBABILITY
Similar Questions
If P and Q are the middle points of the sides BC and CD of the parallelogram ABCD, then AP+AQ is equal to
View SolutionP and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CQ is parallel to AP.
View SolutionP and Q are the mid-point of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PQRS is a parallelogram.
 View Solution
View SolutionE and F are points on diagonal AC of a parallelogram ABCD such that AE=CF. Show that BFDE is a parallelogram.
View SolutionPoints P and Q have been taken on opposite sides AB and CD, respectively of a parallelogram ABCD such that AP=CQ. Show that AC and PQ bisect each other.
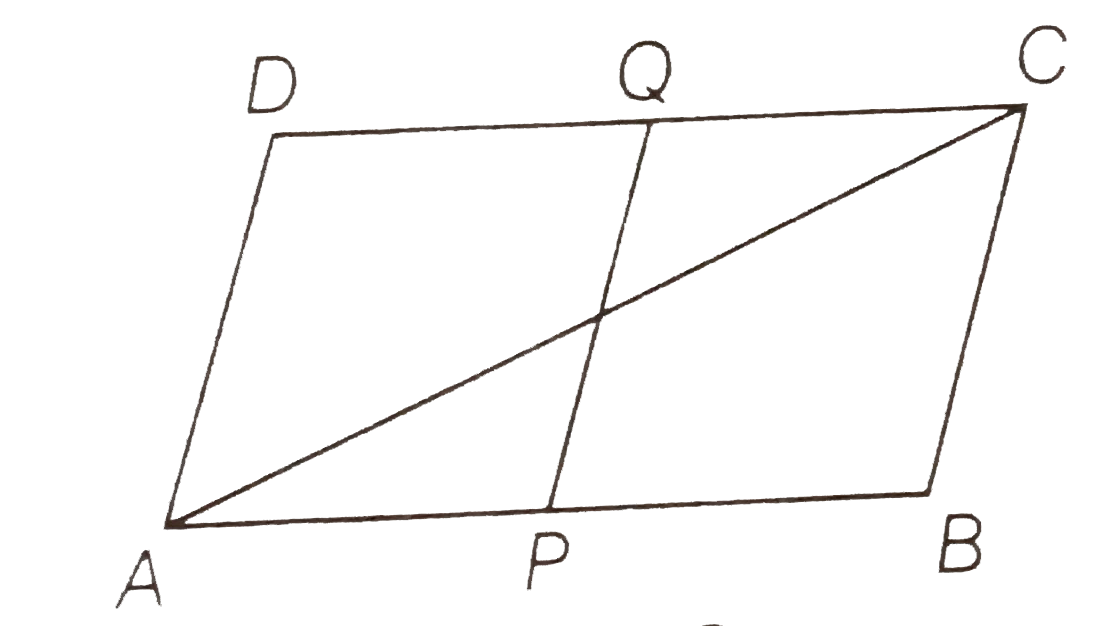 View Solution
View SolutionP and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
View SolutionIn figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP=∠DAP. Prove that AD = 2CD.
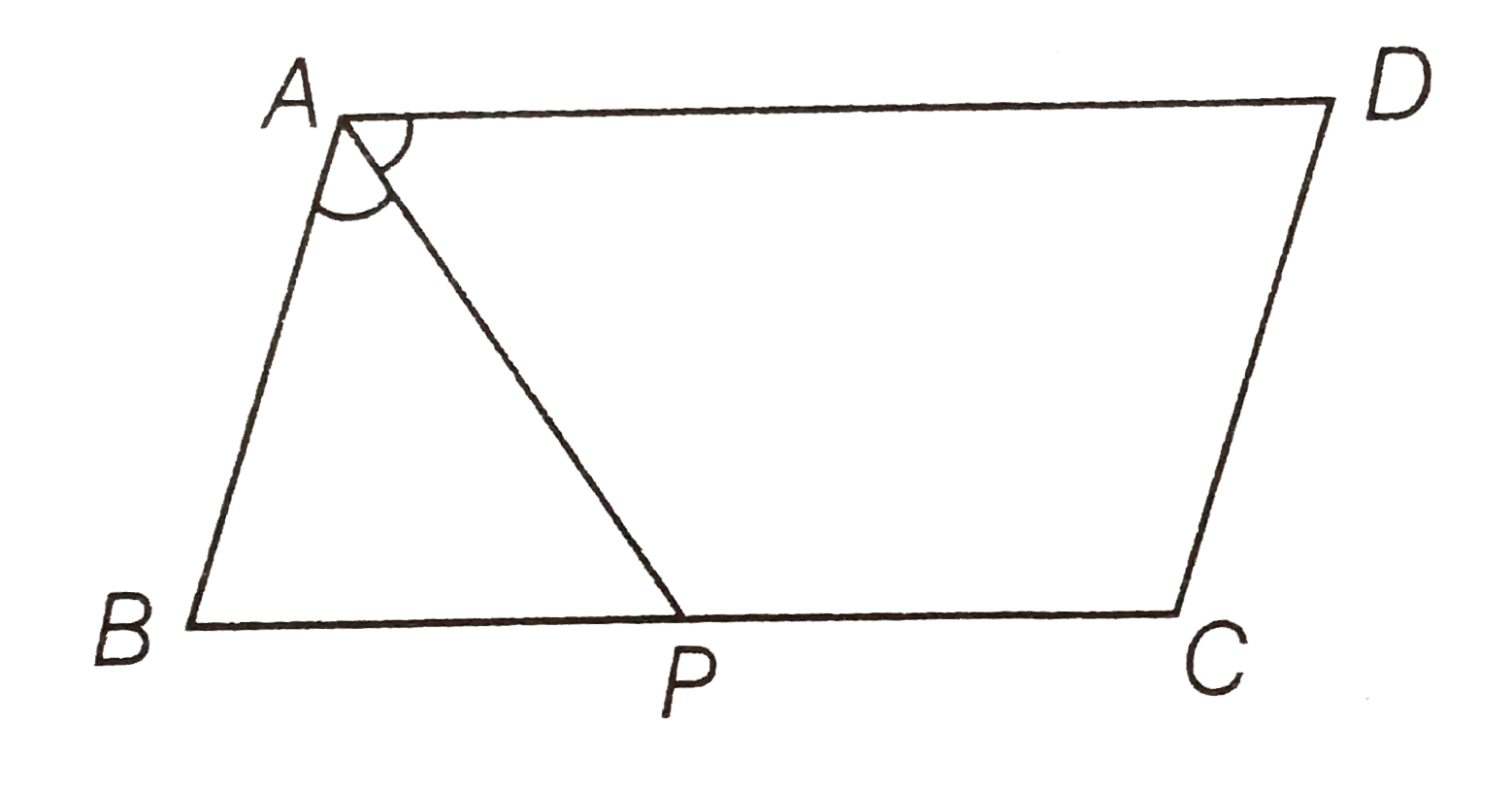 View Solution
View SolutionDiagonals AC and BD of a parallelogram ABCD intersect each other at O. If OA= 3 cm and OD = 2 cm, determine the lengths of AC and BD.
View SolutionA circle intersects the side AD of a parallelogram ABCD at P and BC produced at Q. Prove that square PDQC is cyclic .
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides BC and AD respectively. Show that the line segment BF and ED trisect the diagonal AC.
View Solution

