Complete Solutions to प्रश्नावली 9.3 of chapter समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल |
| NCERT EXEMPLAR HINDI | प्रश्नावली 9.3 |
| Number Of Questions | 9 |
| Academic Year | 2023-24 |
आकृति में, PSDA एक समांतर चतुर्भुज है। PS पर बिंदु Q और R इस प्रकार लिए गए है कि `PQ=QR=RS` है। तथा `PA||QB||RC` है। सिद्ध कीजिए कि ar (PQE) = ar (CFD) है।
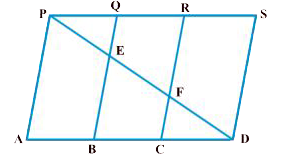
View SolutionX और Y त्रिभुज LMN की भुजा LN पर स्थित दो बिंदु इस प्रकार है कि `LX=XY=YN` है। X से होकर जाती हुई एक रेखा LM के समांतर खींची गई जो MN को Z पर मिलती है। सिद्ध कीजिए कि ar (LZY) = ar (MZYX) है।
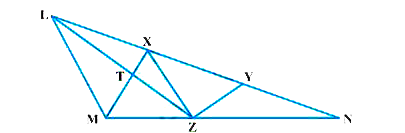
View Solutionसमांतर चतुर्भुज ABCD का क्षेत्रफल `90cm^(2)` है। ज्ञात कीजिए :
(i) ar (ABEF)
(ii) ar (ABD)
(iii) ar (BEF)
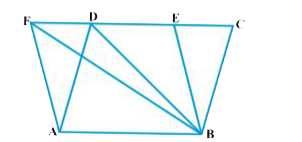
View Solution`DeltaABC`, D भुजा AB का मध्य-बिंदु है तथा P भुजा BC पर स्थित कोई बिंदु है। यदि रेखाखण्ड `CQ||PD` भुजा AB से Q पर मिलता है, तो सिद्ध कीजिए कि ar (BPQ) = `(1)/(2)` ar (ABC) है।
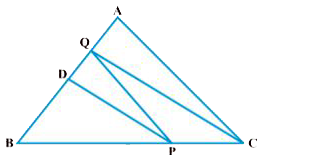
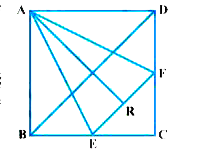
View SolutionABCD एक वर्ग है। E और F क्रमशः BC और CD भुजाओ के मध्य-बिंदु है। यदि R रेखाखण्ड EF का मध्य-बिंदु है तो सिद्ध कीजिए कि ar (AER) = ar (AFR) है।
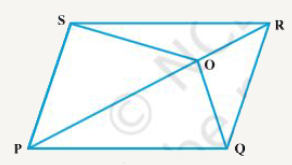
View SolutionO एक समांतर चतुर्भुज PQRS के विकर्ण PR पर स्थित कोई बिंदु है। सिद्ध कीजिए कि ar (PSO) = ar (PQO) है।
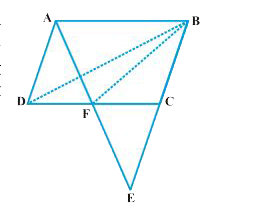
View SolutionABCD एक समांतर चतुर्भुज है, जिसमे BC को E तक इस प्रकार बढ़ाया गया है कि `CE = BC` है। AE भुजा CD को F पर प्रतिच्छेद करती है। यदि ar (DFB) = `3cm^(2)` है, तो समांतर चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए।
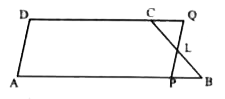
View Solutionएक समलम्ब चतुर्भुज ABCD में AB||DC है तथा L भुजा BC का मध्य बिन्दु है। L से होकर, एक रेखा PQ||AD खींची गई है, जो AB को P पर और बढ़ाई गई DC को Q पर मिलती हैं (चित्र देखिए), सिद्ध कीजिए कि ar(ABCD) = ar(APQD)
View Solutionयदि किसी चतुर्भुज की भुजाओ के मध्य-बिंदुओं को क्रम से मिलाया जाता है, तो सिद्ध कीजिए कि इस प्रकार बने समांतर चतुर्भुज का क्षेत्रफल दिय हुए चतुर्भुज के क्षेत्रफल का आधा होता है।
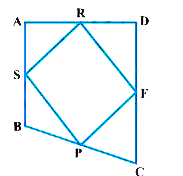
View Solution
प्रश्नावली 9.3 questions and complete solutions for chapter समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल of NCERT EXEMPLAR HINDI of Class 9