Complete Solutions to उदाहरण of chapter सांख्यिकी of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | सांख्यिकी |
| NCERT HINDI | उदाहरण |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
गणित की परीक्षा में 10 विद्यार्थियों द्वारा प्राप्त किए गए अंक लीजिएः
`{:(55, 36, 95, 73, 60, 42, 25, 78, 75, 62):}`
इस रूप में प्रस्तुत किए गए आंकड़ों को यथाप्राप्त आंकड़ें (raw data) कहा जाता हैं ।
क्या इस रूप में ऐसे देखकर आप अधिकतम और न्यूनतम प्राप्तांक ज्ञात करने में आपको कुछ समय लगा है? यदि इन प्राप्तांकों को आरोही (ascending) या अवरोही (descending) क्रम में रखा जाए, तो अधिकतम अंक और न्यूनतम अंक ज्ञात करने में काफी काम समय लगेगा? अतः आइए हम प्राप्तांकों को आरोही क्रम में इस प्रकार रखें:
`{:(25, 36, 42, 55, 60, 62, 73, 75, 78, 92):}`
एक प्रकार हम स्पष्टया देख सकते हैं की न्यूनतम प्राप्तांक 25 और अधिकतम प्राप्तांक 95 हैं । आंकड़ों के अधिकतम और न्यूनतम मानों के अंतर को आकंड़ों का परिसर (range) कहा जाता है । अतः यहाँ पर परिसर 95-25 = 70 हैं
आंकड़ों को आरोही क्रम या अवरोही क्रम में लिखने पर काफी समय लग सकता है, विशेष रूप से तब, जबकि प्रयोग में प्रेक्षणों की संख्या अधिक हो, जैसा की अगले उदाहरण में आप देख सकते हैं ।
View Solutionएक विद्यालय की नवीं कक्षा के 30 विद्यार्थियों द्वारा (100 अंकों में से ) प्राप्त किए गए अंक लीजिएः
`{:(10, 20, 36, 92, 95, 40, 50, 56, 60, 70), (92, 88, 80, 70, 72, 70, 36, 40, 36, 40), (92, 40, 50, 50, 56, 60, 70, 60, 60, 88):}`
आपको याद होगा की एक निश्चित अंक प्राप्त करने वाले विद्यार्थियों की संख्या को इस अंक की बारम्बारता (frequency) कहा जाता है । उदहारण के लिए, यहाँ 4 विद्यार्थियों ने 70 अंक प्राप्त किए हैं । अतः ७० अंक की बारंबारता 4 है । आंकड़ों को और अधिक सरल रूप में समझने के लिए इन्हें हम एक सारणी के रूप में लिखते हैं, जैसा क नीचे दिया गया हैः
सारणी 14.1 को अवर्गीकृत बारंबारता बंटन सारणी (ungrouped frequency distribution table) या केवल बारंबारता बंटन सारणी (frequency distribution table ) कहा जाता है । ध्यान दीजिए की इन सारिणियों को बनाने में आप मिलान चिन्हों (tally marks) का प्रयोग कर सकते हैं, जैसा की अगले उदाहरण में दिखाया गया है ।
View Solutionवन महोत्सव के दौरान 100 विद्यालयों में से प्रत्येक विद्यालय में 100 पौधे लगाए गए । एक महीने बाद लागए गए पौधों में से बच गए पौधों की संख्याएँ निम्न थीः
`{:(95, 67, 28, 32, 65, 65, 69, 33, 98, 96), (76, 42, 32, 38, 42, 40, 40, 69, 95, 92), (75, 83, 76, 83, 85, 62, 37, 65, 63, 42), (89, 65, 73, 81, 49, 52, 64, 76, 83, 92), (93, 68, 52, 79, 81, 83, 59, 82, 75, 82), (86, 90, 44, 62, 31, 36, 38, 42, 39, 83), (87, 56, 58, 23, 35, 76, 83, 85, 30, 68), (69, 83, 86, 43, 45, 39, 83, 75, 66, 83),(92, 75, 89, 66, 91, 27, 88, 89, 93, 42),(53, 69, 90, 55, 66, 49, 52, 83, 34, 36):}`
इतनी बड़ी संख्या में आकंड़ों लो इस प्रकार प्रस्तुत करने के लिए की पाठक इसका सरलता से अर्थ निकल सकें, हम इन आंकड़ों को 20-29, 30-39,...,,90-99 जैसे समूहों में रखकर इन्हें छोटा कर लेते हैं । (क्योंकि हमारे आंकड़ें 23 से 98 के बीच हैं ) । इन समूहों को 'वर्ग' (classes) या 'वर्ग अंतराल '(class intervals) कहा जाता है इनके माप (size) है । वर्ग-माप (class-size) या वर्ग चौड़ाई (class width) कहा जाता है, जो कि यहाँ 10 है प्रत्येक वर्ग कि निम्नतम संख्या को निम्न वर्ग सीमा (lower class limit ) और अधिकतम संख्या को उपरि वर्ग सीमा (upper class limit) कहा जाता है । जैसे, वर्ग 20-29 में 20 निम्न वर्ग सीमा है और 29 उपरि वर्ग सीमा है ।
साथ ही, आप यह भी जानते हैं कि मिलान चिन्हों का प्रयोग करके ऊपर दिए गए आंकड़ों को सारणी रूप में प्रस्तुत किया जा सकता है, जैसा कि सारिणी 14.2 में दिखाया गया है ।
आंकड़ों को इस रूप में प्रस्तुत करने से आंकड़ें सरल और छोटे रूप में हो जाते हैं और हम एक ही दृष्टि में उनके मुख्य लक्षणों को देख सकते हैं । इस प्रकार कि सारणी को वर्गीकृत बारंबारता बंटन सारणी (grouped frequency distribution table) कहा जाता है । यहाँ हम यह सरलता से देख सकते हैं कि 8+18+10+23+12 =71 विद्यालयों में 50% या इससे अधिक पौधे बच गए हैं ।
यहाँ हम यह देखते हैं कि ऊपर कि सारणी में वर्ग अनतिव्यापी (non-overlapping) हैं । ध्यान दीजिए कि यहाँ हम छोटे माप लेकर अधिक संख्या में वर्ग ले सकते थे या बड़े माप लेकर कम संख्या में वर्ग ले सकते थे । उदहारण के लिए, अंतराल 22-26, 27-31, यदि हो सकते थे । इस कार्य के लिए विशेष नियम नहीं है । नियम केवल यही है कि वर्ग अतिव्यापी (overlapping) नहीं होने चिहिए।
View Solutionआइए अब हम निम्नलिखित बारंबारता बंटन सारणी लें, जिसमे एक कक्षा के 38 विद्यार्थियों के भर दिए गए हैः
अब, यदि 35.5 kg और 40.5 kg के भार वाले दो और विद्यार्थी इस कक्षा में आ जाएँ तो उन्हें किस वर्ग अंतराल में रखा जाएगा? उन्हें न तो हम उन अंतरालों में रख सकते हैं जिनकी अंतिम संख्या 35 या 40 हैं और न ही इन्हें हम उन अंतरालों में रख सकते हैं जो इनके बाद आते हैं । ऐसा इसलिए है, क्योंकि दो क्रमागत वर्गों (consecutive classes) की उपरि और निम्न सीमाओं के बीच रिक्त स्थान है । अतः इस स्थिति में हमें अंतरालों को विभक्त करना होता है, जिससे की क्रमागत अंतरालों की उपरि और निम्न सीमाएँ समान हो जाएँ । इसके लिए हमें एक वर्ग की उपरि सीमा और उसके बाद के वर्ग की निम्न सीमा के बीच का अंतर ज्ञात करना होता है । तब हम इस अंतर के आधे भाग को प्रत्येक उपरि सीमा में जोड़ देते हैं और बीच इसी राशि को प्रत्येक निम्न सीमा में से घटा देते हैं ।
उदाहरण की लिए, वर्ग 31-35 और 36-40 लीजिए ।
36-40 की निम्न सीमा = 36
31-35 की उपरि सीमा = 35
अंतर = 36-35 = 1
अन्तः, अंतर का आधा `=(1)/(2) = 0.5`
इस प्रकार, वर्ग 31-35 से बना नया वर्ग अंतराल (31-0.5) - (35+0.5) = 30.05 - 35.5 है । इसी प्रकार, 36-40 से बना नया वर्ग अंतराल
= (36-0.5) - (40 + 0.5)
= 35.5 - 40.5
इस प्रक्रिया को आगे बढ़ाने पर निम्नलिखित संतत वर्ग (continuous classes) प्राप्त होते हैं: 30.5-35.5, 35.5-40.5, 40.5-45.5, 45.5-50.5 50.5-55.5, 55.5-60, 60.5-65.5, 65.-70.5, 70.5-75.5
अब हम इन वर्गों में नए विधार्थियों के भार सम्मिलित कर सकते हैं । परन्तु, ऐसा करने से एक और समस्या आती है । वह यह है की 35.5 दोनों ही वर्गों 30.5-35.5 और और 35.5-40.5 में है । वह यह है की आपके विचार से इस भार को किस वर्ग में रखना चिहिए ?
यदि ऐसे दोनों वर्गों में रखा जाए, तो इसकी गिनती दो बार करनी होगी ।
अतः परंपरा के अनुसार, हम 35.5 को वर्ग 35.5-40.5 में रखते हैं न की वर्ग 30.5-35.5 में, इसी प्रकार, 40.5 को वर्ग 40.5-45.5 में रखा जाता है न की वर्ग 35.5-40.5 में ।
अतः नए भार 35.5 kg और 40.5 kg को क्रमशः 35.5-40.5 और 40.5-45.5 में सम्मिलित किया जाएगा । अब इन कल्पनाओं को ध्यान में रखने पर एक नई बारंबारता बंटन सारणी प्राप्त होगी, जैसा की नीचे दिखाई गई हैः
आइए अब हम क्रियाकलाप 1 में आपके द्वारा एकत्रित किए गए आकंड़ों को लें । इस बार हम चाहेंगे की आप इन आकंड़ों को एक बारंबारता बंटन सारणी की रूप में प्रस्तुत करें ।
View Solutionनवीं कक्षा के 40 विद्यार्थियों से उनके जन्म का महीना बताने के लिए कहा गया । एक प्रकार प्राप्त आंकड़ों से निम्नलिखित आलेख बनाया गयाः

उप्पर दिए गए आलेख को देखकर निम्नलिखित प्रशनों के उत्तर दीजिएः
(i) नवंबर के महीने में कितने विद्यार्थियों का जन्म हुआ?
(ii) किस महीने में सबसे अधिक विद्यार्थियों का जन्म हुआ ?
View Solutionएक परिवार ने जिसकी मासिक आय ₹ 20000 है, विभिन्न मदों के अंतरगर्त हर महीने होने वाले खर्च की योजना बनाई थीः
ऊपर दिए गए आकंड़ों का एक दंड आलेख बनाइए।
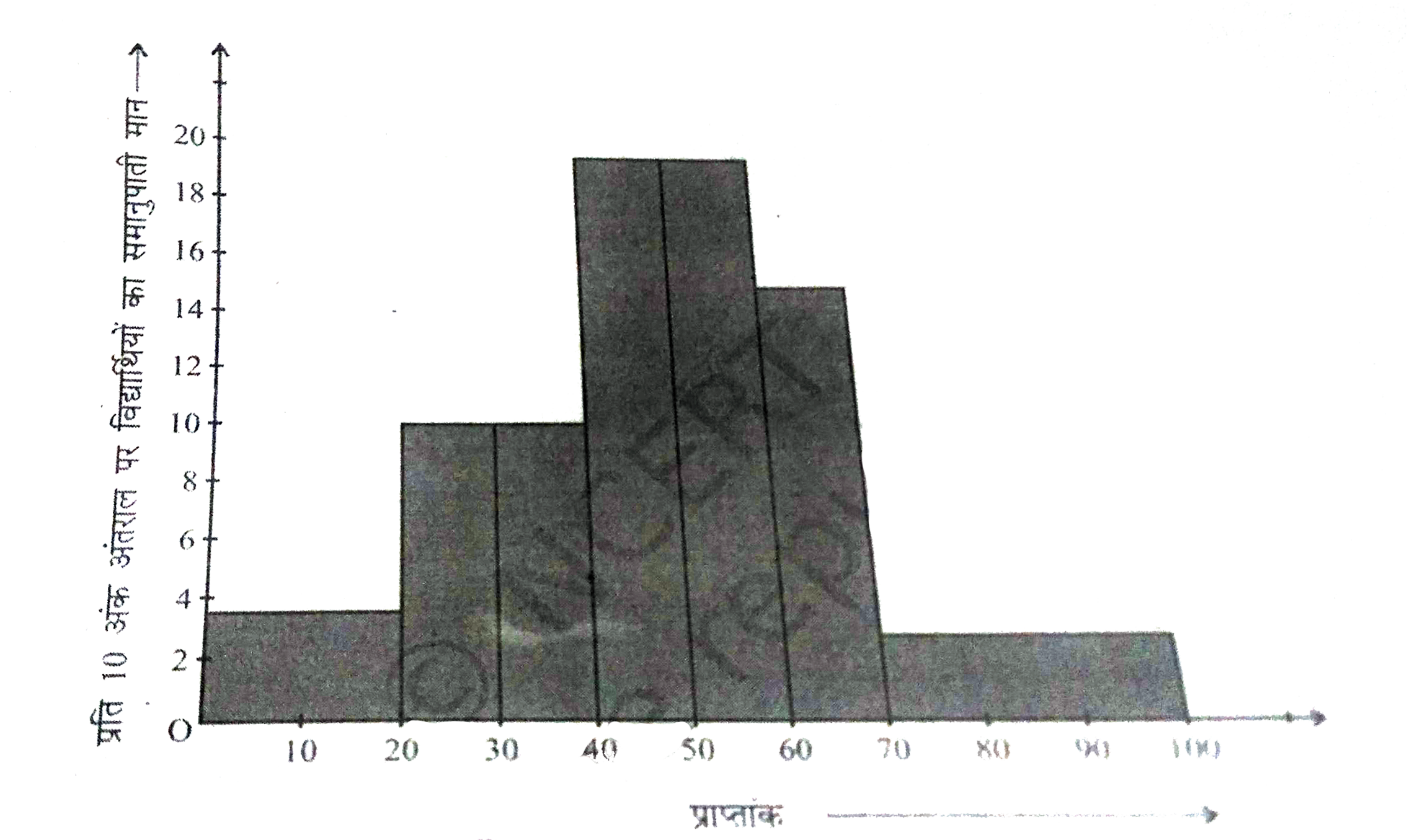
View Solutionएक अध्यापिका दो सेक्शनों के विद्यार्थियों के प्रदर्शनों का विश्लेषण 100 अंक की गणित की परीक्षा लेकर करना चाहती है । उनके प्रदर्शनों को देखने पर वह यह पति है की केवल कुछ ही विद्यार्थियों के प्राप्तांक 20 से कम है और कुछ विद्यार्थियों के प्राप्तांक 70 या उससे अधिक हैं । अतः, उसने विद्यार्थियों को 0-20, 20-30,..., 60-70, 70-100 जैसे विभिन्न माप वाले अंतरालों में वर्गीकृत करने का निर्णय लिया । तब उसने निम्नलिखित सारणी बनाई ।
किसी विद्यार्थी ने इस सारणी का एक आयतचित्र बनाया, जिसे आकृति 14.4 में दिखाया गया है ।

इस आलेखीय निरूपणकी जाँच सावधानी से कीजिए । क्या आप समझते हैं की यह आलेख आकंड़ों का सही-सही निरूपण करता है? इसका उत्तर हैः नहीं । यह आलेख आंकड़ों का एक गलत चित्र प्रस्तुत है । जैसा की हम पहले बता चुके हैं आयतों के क्षेत्रफल आयतचित्र की बारम्बारताओं के समानुपाती होते हैं । पहले इस प्रकार के प्रश्न हमारे सामने नहीं उठे थे, क्योंकि सम्भि आयतों की चौडाईयाँ सामान थी । परन्तु, क्योंकि यहाँ आयतों की चौडाईयाँ बदल रही हैं, इसलिए ऊपर दिया गया आयतचित्र आकंड़ों का एक सही-सही चित्र प्रस्तुत नहीं करता । उदहारण के लिए, यहाँ अंतराल 60 -70 की तुलना में अंतराल 70-100 की बारंबारता अधिक है ।
अतः आयतों की लम्बाइयों में कुछ परिवर्तन (modifications) करने की आवश्यकता होती है, जिससे की क्षेत्रफल पुनः बारम्बारताओं की समानुपाती हो जाये ।
इसके लिए निम्नलिखित चरण लागु करने होते हैः
1. न्यूनतम वर्ग चौड़ाई वाला एक वर्ग अंतराल लीजिए । ऊपर के उदाहरण में, न्यूनतम वर्ग चौड़ाई 10 है ।
2. तब आयतों की लम्बाइयों में इस प्रकार परिवर्तन कीजिए जिससे की वह वर्ग चौड़ाई 10 के समानुपाती हो जाये ।
उदाहरण की लिए, जब वर्ग चौड़ाई 20 होती है, तब आयत की लम्बाई 7 होती है । अतः जब वर्ग चौड़ाई 10 हो, तो आयत की लम्बाई `(7)/(20) xx 10 = 3.5` होगी ।
एक प्रक्रिया को लागू करते रहने पर, हमें निम्नलिखित सारणी प्राप्त होती हैः
क्योंकि हमने प्रत्येक स्थिति में 10 अंकों के अंतराल पर ये लम्बाईयाँ परिकलित की हैं, इसलिए आप यह देख सकते हैं की हम इन लम्बाइयों को 'प्रति 10 अंक अंतराल पर विद्यार्थियों के समानुपाती मान' सकते है ।
परिवर्ती चौड़ाई वाला सही आयतचित्र आकृति 14.5 में दिखाया गया है ।
View Solutionएक परीक्षा में एक कक्षा के 51 विद्यार्थियों द्वारा 100 में से प्राप्त किए अंक सारणी 14.9 में दिए गए हैं। इस बारंबारता बंटन सारणी के संगत बारंबारता बहुभुज बनाइए।
View Solutionएक नगर में निर्वाह खर्च ( cost of living index) का अध्ययन करने निलिखित साप्ताहिक प्रेक्षण किए गए :
ऊपउ दिए गए आंकड़ों का एक बारंबारता बहुभुज ( आयातचित्र बनाए बिना ) खीचिए।
View Solution5 व्यक्तियों के यह कुछ पूछा गया कि अपने समुदाय के सामाजिक कार्य करने में एक सप्ताह में कितना समय देने हैं। उनका कहना था: क्रमश : 10,7,13,20 और 15 घंटे। एक सप्ताह में उनके द्वारा समाजिक कार्य में लगाए समयों का माध्य ( या औसत ) ज्ञात कीजिए।
View Solutionएक विद्यालय की नवीं कक्षा के 30 विद्यार्थियों द्वारा प्राप्त किए गए अंको जो उदाहरण 2 में दिए गए हैका माध्य ज्ञात कीजिए।
View Solutionएक कक्षा के 9 विद्यार्थियों की ( सेंटीमीटरों ) लंबाइयाँ ये हैं :
`144 " "145" "147" "148" "149" "150" "152" "155" "160`
इन आंकडों का माध्य ज्ञात किजिए।
View Solutionकबड्डी की एक टीम द्वारा अनेक मैचों में प्राप्त किए गए अंक ये है:
`17" "2" "7" "27" "15" "5 , "14", "8" , "10", "24", "48" , "10", "8", "7", "18", "28`
टीम द्वारा प्राप्त किए गए अंकों का माध्यक ज्ञात कीजिए।
View Solution20 विद्यार्थियों द्वारा (10 में मे ) प्राप्त किए गए निम्नलिखित अंकों का बहुलक ज्ञात कीजिए।
4, 6, 5, 9, 3, 2, 7, 6, 5, 4, 9, 10, 10, 3, 4, 7, 6, 9, 9
View Solutionएक फैक्टरी की एक छोटी इकाई लीजिए जहाँ 5 व्यक्ति काम करते हैं, जिनमें एक सुपरवाइजर है और चार मजदूर हैं। प्रत्येक मजदूर को प्रति माह Rs 5000 वेतन मिलता है, जबकि सुपरवाइजर को प्रति माह Rs 15000 वेतन लिलता है। फैक्टरी की इस इकाई के वेतनों के माध्य , माध्यक और बहुलक परिकलित कीजिए।
View Solution
उदाहरण questions and complete solutions for chapter सांख्यिकी of NCERT गणित(HINDI) of Class 9