Complete Solutions to EXAMPLES of chapter TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIANGLES |
| NCERT KANNAD | EXAMPLES |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
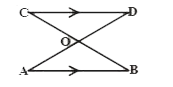
In the given Figure AB and CD are intersecting at ‘O’, OA = OB and OD = OC. Show that (i) `Delta AOD ~= DeltaBOC` and (ii) `AD || BC`.
View SolutionAB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
View SolutionIn the given figure, `AB||DC and AD||BC` show that `DeltaABC ~= Delta CDA`.
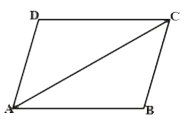
View SolutionIn the given figure, AL || DC, E is mid point of BC. Show that `DeltaEBL ~= DeltaECD`.
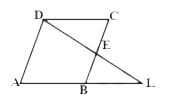
View SolutionUse the information given in the adjoining figure, to prove :
`(i) DeltaDBC ~= DeltaEAC`
`(ii) DC = EC.`
View SolutionLine-segment AB is parallel to another line-segment CD. O is the mid-point of AD.
Show that (i) `DeltaAOB ~= DeltaDOC` (ii) O is also the mid-point of BC.
View SolutionIn `DeltaABC`, the bisector AD of A is perpendicular to side BC Show that AB = AC and `DeltaABC` is isosceles.
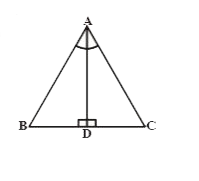
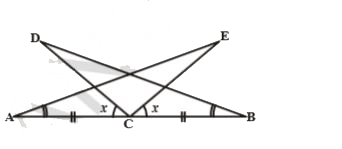
View SolutionIn the adjacent figure, `AB = BC and AC = CD`. Prove that : `/_ BAD : /_ ADB = 3 : 1.`

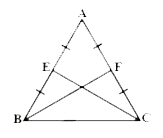
View SolutionE and F are respectively the mid-points of equal sides AB and AC of `DeltaABC` (see figure)
Show that BF = CE.
View SolutionIn an isosceles triangle ABC with AB = AC, D and E are points on BC such that BE = CD (see figure) Show that AD = AE
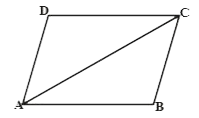
View SolutionIn quadrilateral ABCD, AB = CD, BC=AD show that `DeltaABC ~= DeltaCDA` Consider `DeltaABC and DeltaCDA`
View SolutionAB is a line - segment. P and Q are points on either side of AB such that each of them is equidistant from the points A and B (See Fig ). Show that the line PQ is the perpendicular bisector of AB.
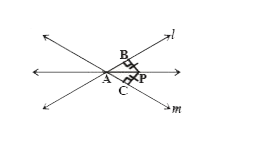
View SolutionP is a point equidistant from two lines l and m intersecting at point A (see figure). Show that the line AP bisects the angle between them.
View SolutionD is a point on side BC ΔABC such that AD = AC (see figure). Show that AB > AD.
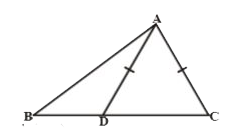
View Solution
EXAMPLES questions and complete solutions for chapter TRIANGLES of NCERT MATHS (KANNADA ENGLISH) of Class 9