Complete Solutions to EXERCISE - 7.1 of chapter TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIANGLES |
| NCERT KANNAD | EXERCISE - 7.1 |
| Number Of Questions | 11 |
| Academic Year | 2023-24 |
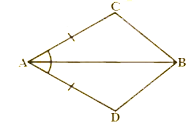
In quadrilateral `ACBD, AC = AD and AB` bisects `/_A` Show that `DeltaABC~= DeltaABD`.
What can you say about BC and BD?
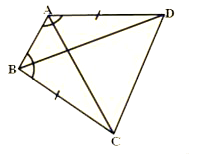
View SolutionABCD is a quadrilateral in which AD = BC and`/_ DAB = /_ CBA` Prove that
`(i) DeltaABD ~= DeltaBAC`
(ii) `BD = AC`
(iii)` /_ ABD = /_ BAC`
View SolutionAD and BC are equal and perpendiculars to a line segment AB. Show that CD bisects AB.
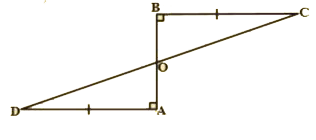
View Solutionl and m are two parallel lines intersected by another pair of parallel lines p and q . Show that `DeltaABC~= DeltaCDA`.

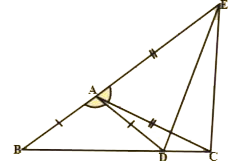
View SolutionIn the adjacent figure, `AC = AE, AB = AD and /_ BAD = /_ EAC`. Show that BC = DE.
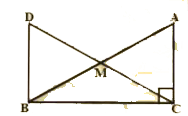
View SolutionIn right triangle ABC, right angle is at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that :
`(i) DeltaAMC ~= DeltaBMD`
`(ii) /_DBC` is a right angle
`(iii) Delta DBC ~= DeltaACB` (iv)`CM = 1/2 AB`.
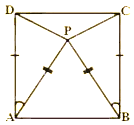
View SolutionIn the adjacent figure ABCD is a square and `Delta APB` is an equilateral triangle. Prove that` DeltaAPD ~= DeltaBPC`.
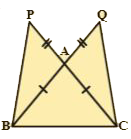
View SolutionIn the adjacent figure `DeltaABC` is isosceles as `bar(AB) = bar(AC), bar(BA) and bar(CA)` are produced to Q and P such that `bar(AQ) = bar(AP)`. . Show that `bar(PB) = bar(QC)`.
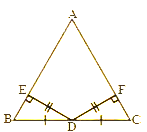
View SolutionIn the adjacent figure `DeltaABC, D` is the midpoint of BC. `DE_|_AB, DF_|_AC` and `DE = DF`. Show that `DeltaBED ~= Delta CFD`.
View SolutionIf the bisector of an angle of a triangle also bisects the opposite side, prove that the triangle is isosceles.
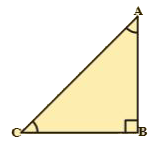
View SolutionIn the given figure ABC is a right triangle and right angled at B such that `/_BCA = 2/_BAC.`
Show that hypotenuse AC = 2BC.
View Solution
EXERCISE - 7.1 questions and complete solutions for chapter TRIANGLES of NCERT MATHS (KANNADA ENGLISH) of Class 9