Complete Solutions to Exercise 7.3 of chapter TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIANGLES |
| Mathematics | Exercise 7.3 |
| Number Of Questions | 5 |
| Academic Year | 2023-24 |
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
View Solution`DeltaA B C`and `DeltaD B C`are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that (i) `\ DeltaA B D~=DeltaA C D`
(ii) `DeltaA B P~=DeltaACP`
(iii) `AP` bisects `∠ A` as well as `∠ D`
(iv) `AP` is the perpendicular bisector of `BC`

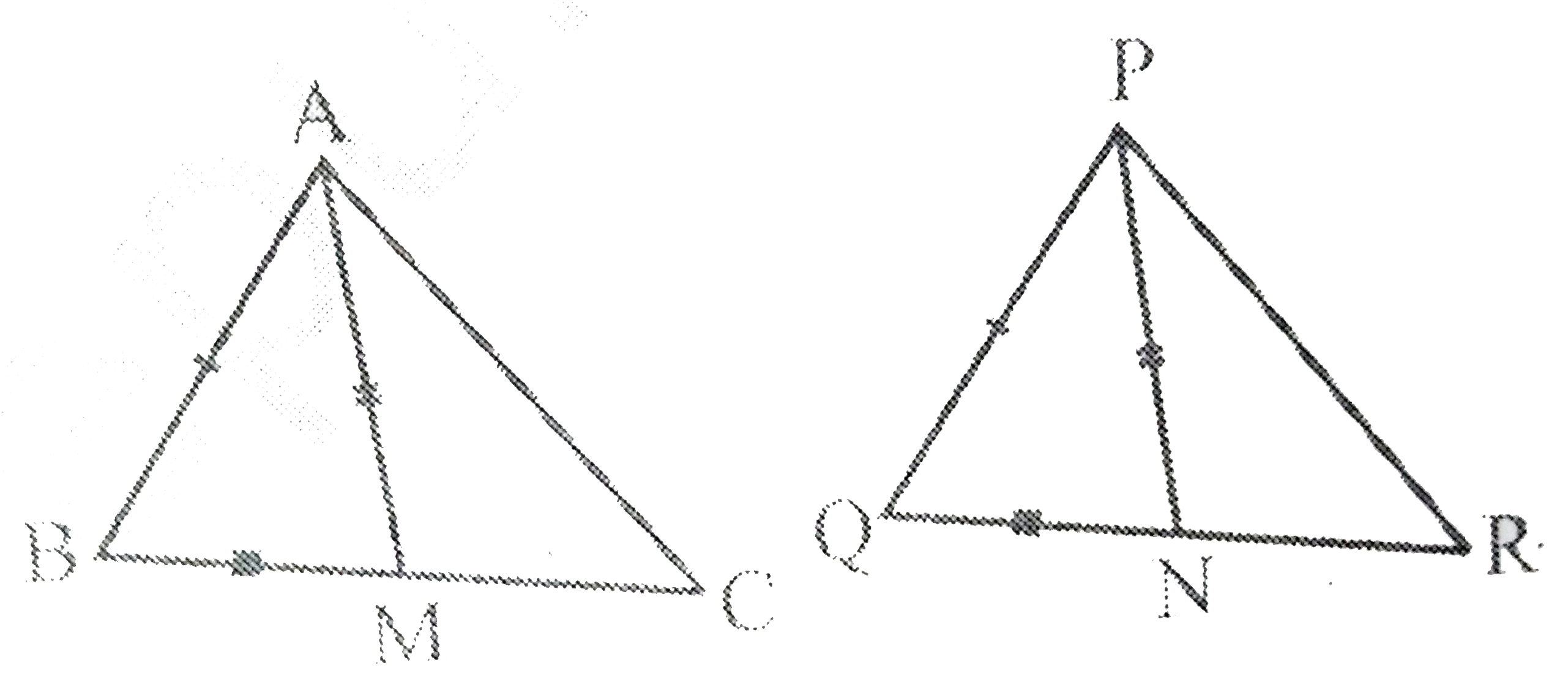
View SolutionTwo sides `AB` and `BC` and median `AM` of one triangle ABC are respectively equal to side `PQ` and `QR` and median `PN` of `DeltaA B C~=DeltaP Q R`(see Fig. 7.40). Show that:
(i) `DeltaA B M~=DeltaP Q N`
(ii) `DeltaA B C~=DeltaP Q R`
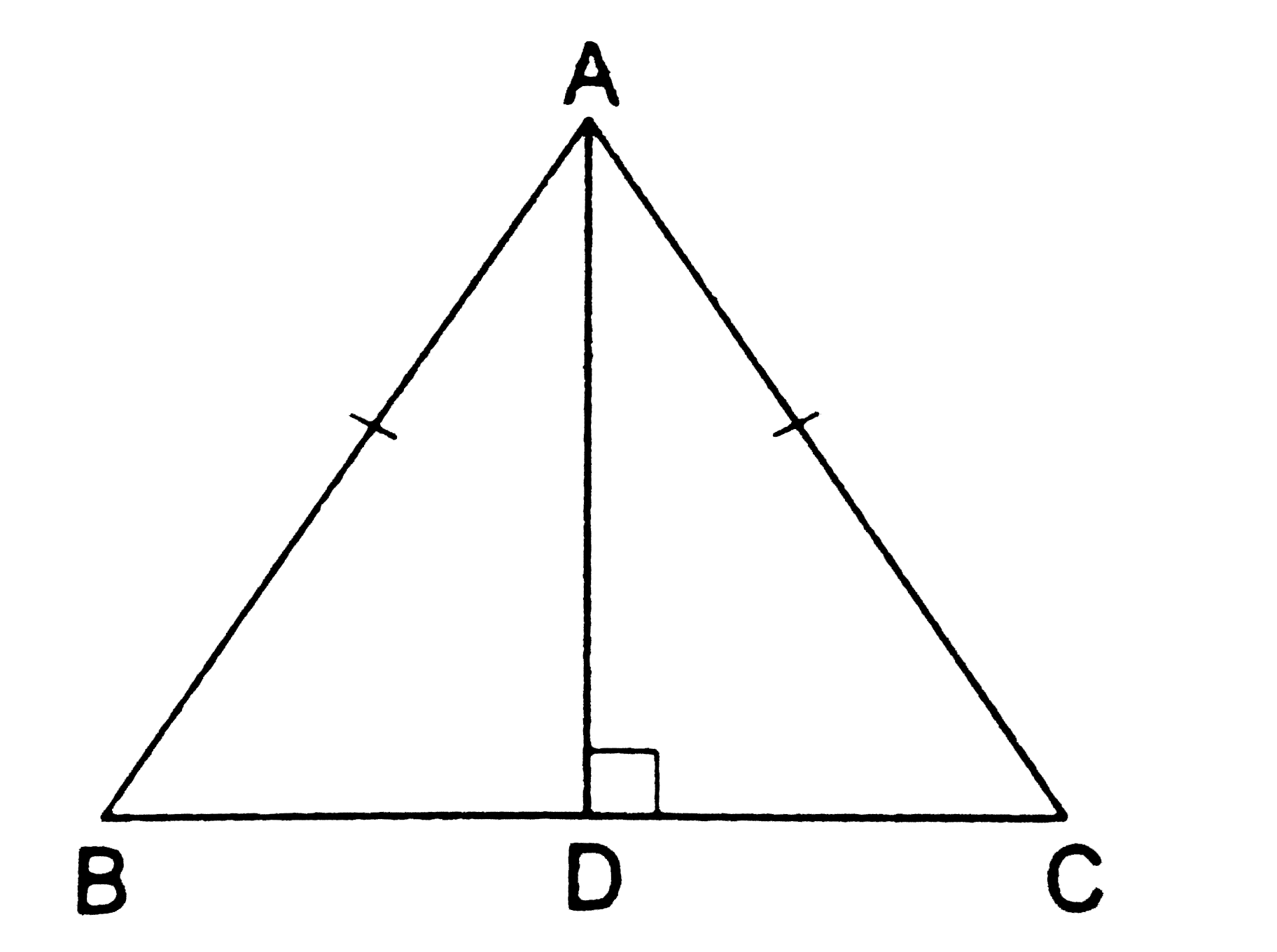
View SolutionAD is an altitude of an isosceles `DeltaABC` in which AB = AC.
Show that (i) AD bisects BC,
(ii) AD bisects `angleA`.
View SolutionABC is an isosceles triangle with `A B =\ A C`. Draw `A P_|_B C` to show that `/_B =/_C.`
View Solution
Exercise 7.3 questions and complete solutions for chapter TRIANGLES of NCERT MATHEMATICS(HINGLISH) of Class 9