ABC is an isosceles triangle with AB= AC. Draw AP⊥BC to show that ∠B=∠C.
To solve the problem, we need to show that in triangle ABC, where AB = AC (making it isosceles), the angles at B and C are equal. We will achieve this by constructing a perpendicular from A to BC, denoted as AP, and then proving that triangles ABP and ACP are congruent.
1. Draw Triangle ABC: Start by drawing triangle ABC such that AB = AC. Label the points accordingly.
2. Draw Perpendicular AP: From point A, draw a perpendicular line to line segment BC, meeting BC at point P. This means that AP is perpendicular to BC.
3. Identify the Right Angles: Since AP is perpendicular to BC, we have that angle APB = 90° and angle APC = 90°.
4. Analyze Triangles ABP and ACP: We will now consider triangles ABP and ACP. We need to show that these two triangles are congruent.
5. List the Sides and Angles:
- Common Side: AP is common to both triangles, so AP = AP.
- Given Side: We know that AB = AC (since triangle ABC is isosceles).
- Right Angles: We have already established that angle APB = angle APC = 90°.
6. Apply the RHS Criterion: Since we have:
- One side (AP) is equal in both triangles,
- The other side (AB = AC) is given,
- The angle (APB = APC) is 90°,
We can conclude that triangles ABP and ACP are congruent by the RHS (Right angle-Hypotenuse-Side) criterion.
7. Conclude Angles: By the property of congruent triangles (CPCTC - Corresponding Parts of Congruent Triangles are Congruent), we can state that angle B = angle C.
Final Statement:
Thus, we have shown that in triangle ABC, with AB = AC, the angles at B and C are equal, i.e., ∠B = ∠C.
---
- Common Side: AP is common to both triangles, so AP = AP.
- Given Side: We know that AB = AC (since triangle ABC is isosceles).
- Right Angles: We have already established that angle APB = angle APC = 90°.
- One side (AP) is equal in both triangles,
- The other side (AB = AC) is given,
- The angle (APB = APC) is 90°,
We can conclude that triangles ABP and ACP are congruent by the RHS (Right angle-Hypotenuse-Side) criterion.
Thus, we have shown that in triangle ABC, with AB = AC, the angles at B and C are equal, i.e., ∠B = ∠C.
Topper's Solved these Questions
Similar Questions
ABC is an isosceles triangle with AB= AC. Draw AP⊥BC to show that ∠B=∠C.
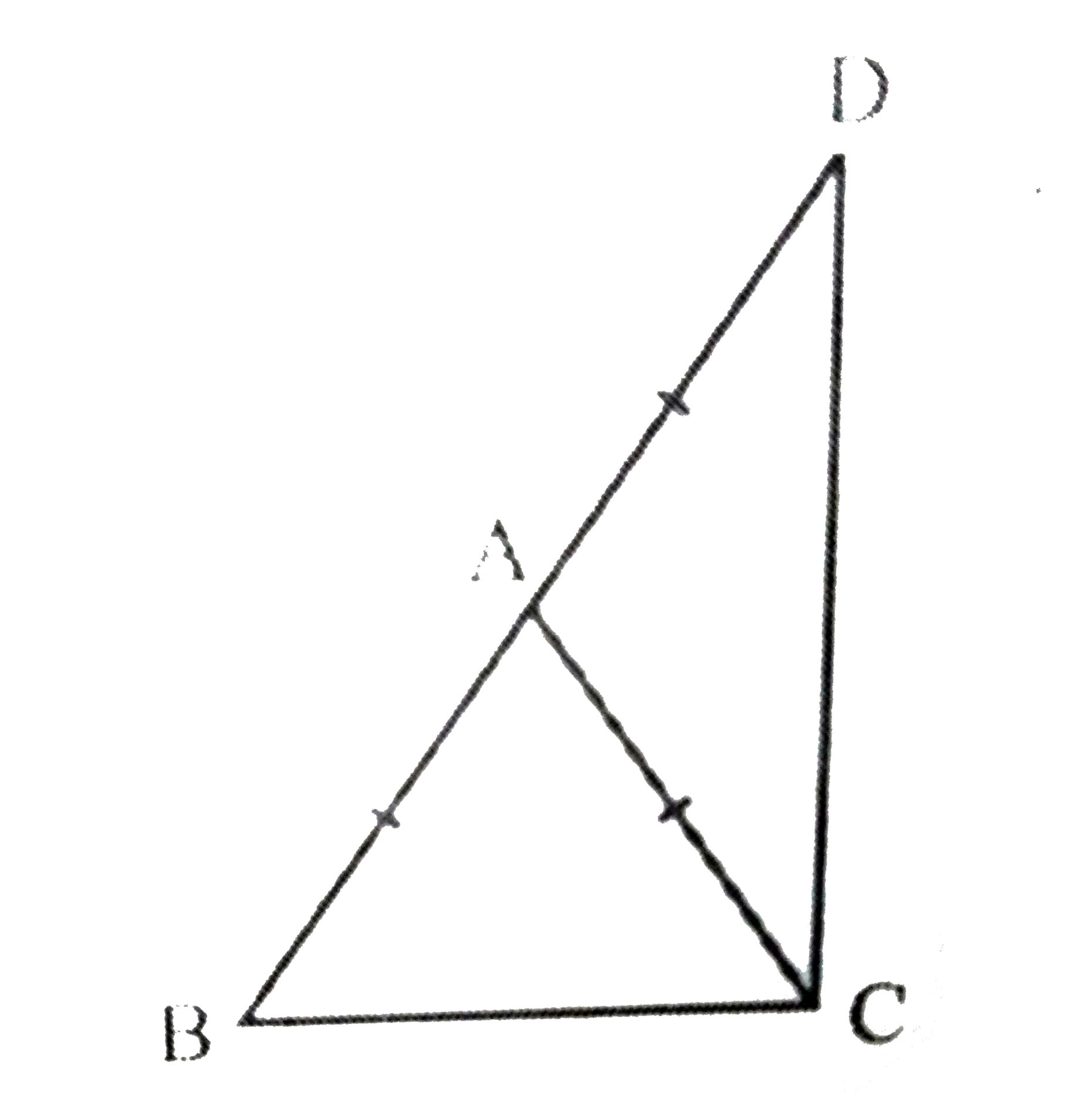
View SolutionΔABC is an isosceles triangle in which AB=AC. Side BA is produced to D such that AD=AB (see Fig. 7.34). Show that ∠BCD is a right angle.
 View Solution
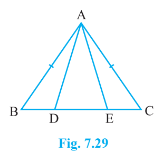
View SolutionIn an isosceles triangle ABC with AB=AC, D and E are points on BCsuch that BE=CD(see Fig. 7.29). Show that AD=AE
 View Solution
View SolutionIn Figure, ABC is an isosceles triangle in which AB=AC.CPparel≤lAB and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA and (ii) ABCP is a parallelogram.
 View Solution
View SolutionABC is an isosceles triangle in which AB=AC. AD bisects exterior angle PAC and CD∣∣AB. Show that(i) ∠DAC=∠BCA and (ii) ABCD is a parallelogram.
View SolutionIn an isosceles triangle ABC, with AB=AC, the bisectors of B and C intersect each other at O. Join A to O. Show that :
(i) OB=OC
(ii) AO bisects AView SolutionThe bisectors of ∠Band∠C of an isosceles ΔABC with AB=AC intersect each other at point O. Show that the exterior angle adjacent to ∠ABC is equal to ∠BOC.
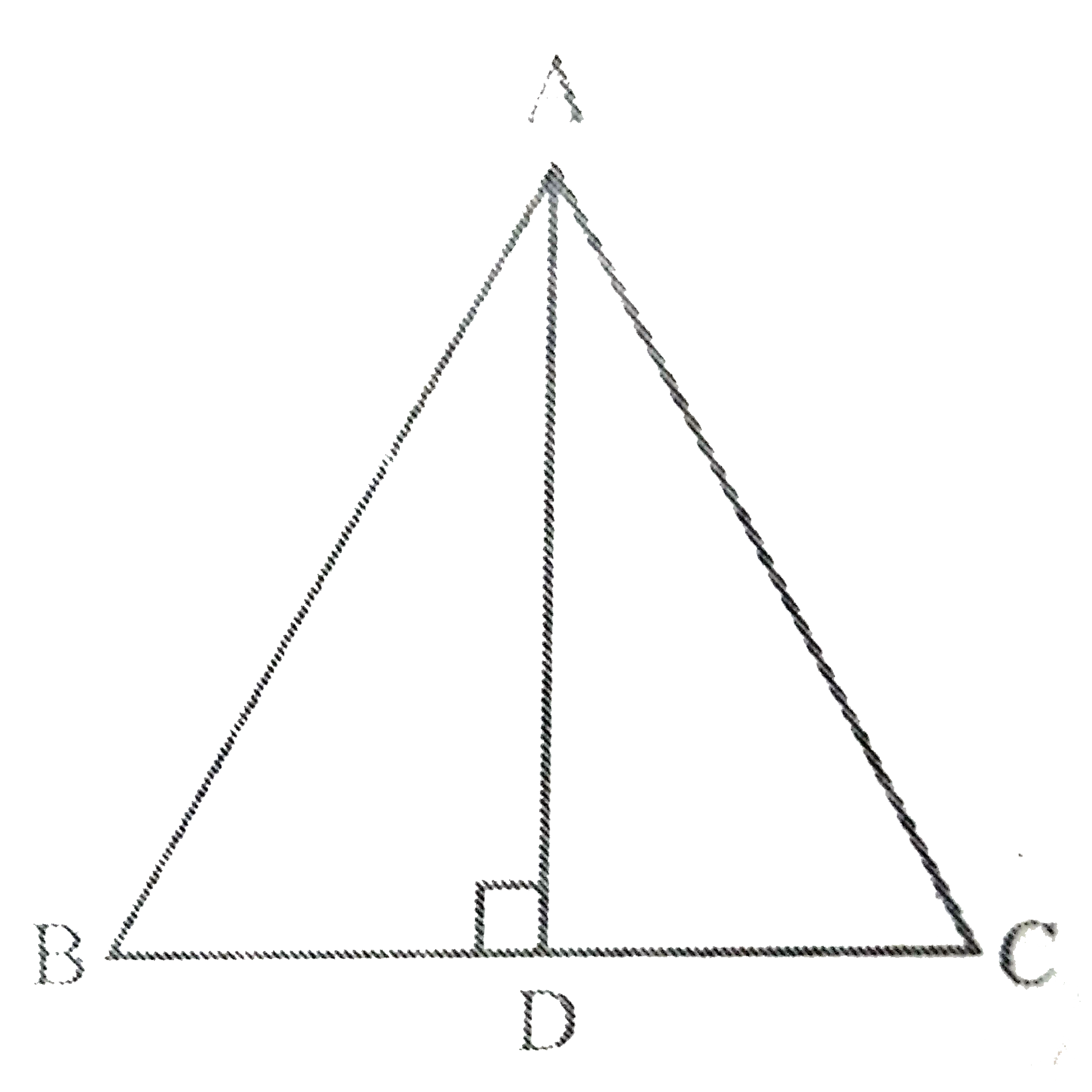
View SolutionIn ΔABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that ΔABCis an isosceles triangle in which AB = AC.
 View Solution
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that ABD ≅ACD (ii) ABP ≅ACP
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that AP bisects \ ∠A as well as ∠D AP is the perpendicular bisector of BC
View Solution

